Gravitation: Vom Fahrstuhl zur Raumzeitkrümmung
Was ist in Einsteins Theorie denn nun eigentlich Gravitation?
Ein Artikel von Markus Pössel
Was ist Gravitation? Einsteins Allgemeine Relativitätstheorie hat auf diese Frage eine ungewohnte Antwort parat, um die es in diesem Vertiefungsthema gehen soll: Zum Teil ist Gravitation eine Illusion, zum Teil assoziiert mit einer Eigenschaft namens „Krümmung“. Insgesamt ist Gravitation ein Aspekt der Geometrie von Raum und Zeit.
Freier Fall
Eine wichtige Besonderheit der Gravitationskraft ist, dass sie alle Körper (genauer: alle Testkörper) gleich schnell fallen lässt. Eine Feder und eine Kanonenkugel fallen mit haargenau derselben Beschleunigung zu Boden (zumindest in einem Vakuumbehälter, in dem es keine Luftreibungskräfte gibt).
Das heißt umgekehrt, dass es für einen Forscher, der in einer fensterlosen Kabine eingeschlossen ist, unmöglich ist, festzustellen, ob sich die Kabine im leeren Weltraum befindet, fernab aller Gravitationsquellen, oder aber im freien Fall in einem konstanten Schwerefeld. In beiden Situationen schwebt der Forscher schwerelos in der Kabine.
Wir kennen diese Situation von den irdischen Raumfahrern, die sich schließlich mitnichten aus dem Einflussbereich der Erd- oder Sonnenschwerkraft entfernen, sondern sich in besonderen Spielarten des freien Falls befinden, etwa in einer Umlaufbahn um die Erde. Das folgende Foto etwa zeigt den Wissenschaftsastronauten C. Michael Foale an Bord der internationalen Raumstation ISS mit zwei freischwebenden Grapefruits.

Astronaut C. Michael Foale auf der ISS
© NASA
Unter diesen Umständen sollte sich die Physik in der frei fallenden Kabine mit den Gesetzen der Speziellen Relativitätstheorie beschreiben lassen – denselben Gesetzen, wie sie für Beobachter gelten, die fern aller Gravitationsquellen im freien Raum schweben. (Diese Aussage ist auch als Äquivalenzprinzip bekannt; weitergehende Informationen bietet das Vertiefungsthema Kabine, Schwerkraft und Rakete: Das Äquivalenzprinzip.)
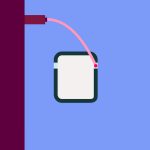
Ist die Gravitation damit nur eine Scheinkraft? Für die fast konstante Schwerkraft, die wir auf der Erdoberfläche gewohnt sind, könnte man so argumentieren, denn drehen wir den Spieß einmal um und stellen uns die hier skizzierte Situation vor:
Nehmen wir an, wir gehörten zur Besatzung der Raumstation, die rechts zu sehen ist, und die fernab aller Gravitationsquellen frei durch den Weltraum treibt. Nun kommt, links zu sehen, ein Beobachter auf einer raketenbetriebenen Raumstation daher, die mit 9,81 Meter pro Sekundenquadrat beschleunigt wird. Ein Beobachter auf der beschleunigten Raumstation fühlt sich bei diesem Beschleunigungswert genauso schwer wie wir auf der Erdoberfläche: Auch die Schwerebeschleunigung, mit der Objekte nahe der Erdoberfläche zu Boden fallen, beträgt 9,81 Meter pro Sekundenquadrat.
Genau wie für einen Erdbewohner gibt es für diesen Beobachter ein ganz klares Unten und Oben – Unten ist, wohin alle Körper fallen, und Oben ist die Gegenrichtung. Wenn er in seiner raketenbetriebenen Station nach oben schaut, sieht der Beobachter die anderen Raumstationen so schnell in Richtung des Bodens seiner eigenen Raumstation „fallen“, wie wir Objekte in Richtung Erdboden fallen sehen. Und dennoch ist in dieser Situation nirgends Schwerkraft am Werk. Die Beobachter in den frei treibenden, unbeschleunigten Raumstationen sind sich einig: Allein der Umstand, dass der betreffende Beobachter die Welt von einem beschleunigten Bezugssystem aus betrachtet, ist Schuld daran, dass es für ihn so aussieht, als würden alle Objekte „zu Boden fallen“, und sein „Oben“ ist gerade die Richtung, in welche die Rakete beschleunigt wird. Sobald das Raketentriebwerk abgeschaltet wird, ist der Spuk vorbei, und kein Objekt „fällt“ mehr nach unten.
Verhält es sich mit der Schwerkraft auf der Erde genauso? Ist sie letztendlich nur eine Folge des unnatürlich-beschleunigten Bezugssystems, von dem aus wir die Welt beobachten – und verschwindet, sobald wir zu einem frei fallenden Bezugssystem übergehen?
Was an Schwerkraft übrig bleibt
Tatsächlich lässt sich die Schwerkraft der Erde auch beim Übergang in ein frei fallendes Bezugssystem nicht vollständig beseitigen (sie lässt sich nicht „wegtransformieren“, wie Physiker sagen würden).
Um das zu sehen, betrachten wir eine frei fallende, aber gigantisch große Kabine, und darin schwebend zwei riesige Bälle. Was passiert, wenn diese Kabine Richtung Erde fällt, zeigt die folgende Animation:
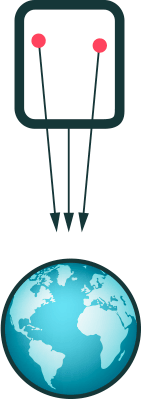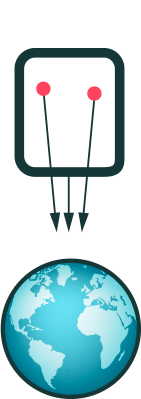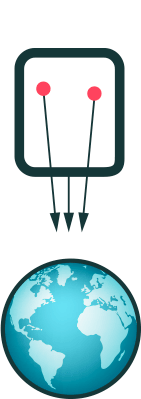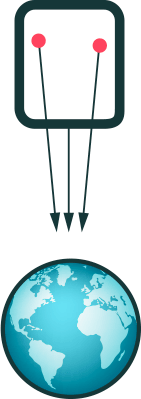
Hier wirkt sich aus, dass Körper, die auf die Erde zu fallen, nicht in ein und dieselbe Richtung fallen („unten“), sondern auf ein und denselben Raumpunkt zu, nämlich den Erdmittelpunkt. Selbst aus Sicht des mit der Kabine frei fallenden Beobachters wirkt sich die Erdschwerkraft daher ein wenig aus. Den Fall der Bälle nach unten bekommt dieser Beobachter zwar nicht mit, da er selbst in seiner Kabine nebenherfällt. Dass sich die beiden Bälle dabei etwas näher kommen, sieht er dagegen sehr wohl.
Grund des Näherkommens ist, dass die Schwerkraft, die auf den linken Ball wirkt, eine etwas andere Richtung hat als die auf den rechten. Für die Annäherung verantwortlich ist die Differenz der beiden Kräfte, eine sogenannte Gezeitenkraft. (Namensgebend ist dabei der leichte Kraftunterschied, mit dem die Gravitationskraft des Mondes auf die Erde, auf die dem Mond zugewandten und die ihm abgewandten Ozeane wirkt – dieser Kraftunterschied ist verantwortlich für die Gezeiten, für Ebbe und Flut.)
Noch drastischer werden die Auswirkungen der Schwerkraft, wenn ein Kabinenbewohner seine Beobachtungen auf diejenigen Körper ausdehnt, die sich auf der anderen Seite der Erde befinden. Sicher, die direkt neben ihm fallenden Körper verhalten sich so, als gäbe es keine Schwerkraft. Doch die Körper auf der anderen Seite der Erde fallen sogar mit dem Doppelten der üblichen Schwerebeschleunigung auf solch einen Beobachter zu!
All das zeigt die Unterschiede zu der im letzten Abschnitt behandelten Situation eines beschleunigten Beobachters im gravitationsfreien Raum auf. Solch ein Beobachter musste nur sein Bezugssystem wechseln – das Raketentriebwerk seiner Raumstation abschalten – und schon verschwand das, was er vorher als konstante „Schwerkraft“ wahrgenommen hatte. Die Erdschwerkraft dagegen lässt sich durch den Übergang in ein frei fallendes Bezugssystem nicht vollständig zum verschwinden bringen. In einer kleinen, frei fallenden Kammer, in der wir das Geschehen nur eine kurze Zeit verfolgen, ist der Unterschied zum gravitationsfreien Raum zwar verschwindend gering. Doch je größer der betrachtete Raumzeitbereich ist, je größer unsere Fahrstuhlkabine ist, je länger wir beobachten, umso deutlicher werden die Gezeitenkräfte – der auch im freien Fall nachweisbare „Rest an Schwerkraft“.
Papier und Kugel
Bemerkenswerterweise gibt es zu dieser Doppelnatur der Gravitation – zum Teil eine Scheinkraft, zum Teil eine Gezeitenkraft – eine Entsprechung in der reinen Mathematik, genauer: in der Geometrie verzerrter oder gekrümmter Flächen.
Die einfachste zweidimensionale Oberfläche ist die flache Ebene – das unendlich ausgedehnte Analogon eines flachen Blattes Papier. Die kürzeste Verbindung zweier Punkte in der Ebene ist ein Wegstück entlang der Geraden, auf der die beiden Punkte liegen. Aus solchen geraden Strecken lassen sich geometrische Figuren zusammensetzen, etwa Dreiecke. Für sie gelten die Beziehungen der ebenen Geometrie, wie sie die meisten Leser aus der Schule kennen dürften – vom Strahlensatz über den Satz des Pythagoras bis hin zu dem Umstand, dass die Winkelsumme in jedem Dreieck 180 Grad beträgt:
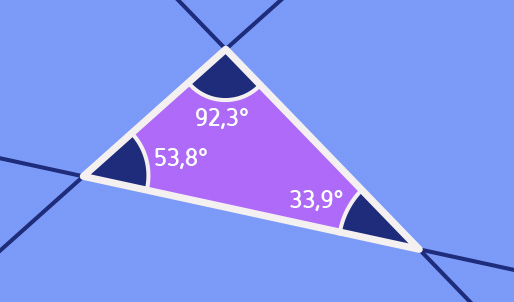
Ebenes Dreieck; Winkelsumme
Doch eine perfekte Ebene ist nur der einfachste Fall einer Fläche. Allgemeinere Oberflächen, etwa eine Kugelfläche, eine Sattelfläche, oder die sanft gewellte Fläche, die zurückbleibt, wenn sich bei Ebbe das Wasser aus dem Wattenmeer zurückgezogen hat, haben nicht mehr dieselben geometrischen Eigenschaften wie eine Ebene. Ein Beispiel für eine Fläche, die nicht eben, sondern gekrümmt ist, ist die Oberfläche einer Kugel. In einer Kugeloberfläche gibt es keine Geraden, allenfalls geradestmögliche Kurven. Solche geradestmöglichen Kurven in einer Fläche werden Geodäten genannt. Im Falle der Kugel sind die Geodäten die so genannten Großkreise (beispielsweise der Äquator). Die kürzeste Verbindung zwischen zwei Punkten auf der Kugeloberfläche führt entlang des Großkreises, entlang der Geodäte, auf der die beiden Punkte liegen.
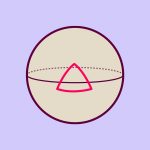
Die folgende Abbildung zeigt eine Kugel sowie, in grün, ein durch Geodätenabschnitte gebildetes Dreieck:

Kugel mit geodätischem Dreieck
Allein die zwei rechten Winkel am Äquator (rote Linie) addieren sich schon zu 180 Grad. Die Winkelsumme des gesamten Dreiecks, bei der noch der Winkel an der Dreiecksspitze am Nordpol hinzukommt, ist somit deutlich größer als 180 Grad. Tatsächlich lässt sich mit Hilfe dieses Winkelüberschusses ein exaktes Maß für die Krümmung der Kugel (und damit der Abweichung ihrer Geometrie von jener der Ebene) definieren.
Wo ist die Krümmung?
Trotz der Unterschiede zwischen den verschiedenen Geometrien – hie die Ebene, dort gekrümmte Flächen – gilt ganz allgemein folgendes: Wenn man beispielsweise einen winzig kleinen Oberflächenausschnitt einer Kugel mit der Lupe betrachtet, dann ist er kaum zu unterscheiden von einer kleinen Region eines flachen Blattes Papier. Wir nutzen diesen Umstand fast täglich aus – einen Stadtplane, der nur einen winzigen Ausschnitt der Erdoberfläche zeigt, erstellen und lesen wir so, als habe die Stadtfläche dieselbe Geometrie wie das flache Blatt Papier, auf das der Plan gedruckt ist:
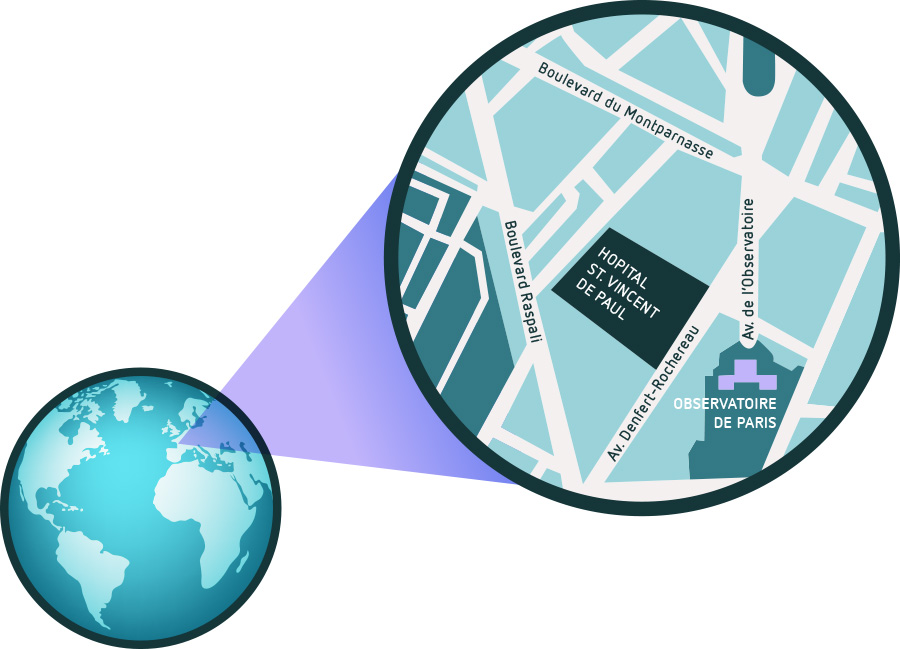
Diese Vorgehensweise ist durchaus erfolgreich, obwohl unsere Städte in Wirklichkeit nicht auf einer gigantischen Ebene, sondern auf der Oberfläche einer gigantischen Kugel angesiedelt sind. Erst bei größeren Oberflächenregionen macht sich bemerkbar, dass die Kugel gekrümmt ist; je ausgedehnter die Region, umso deutlicher merkbar die Krümmung.
Dasselbe gilt für jede glatte, gekrümmte Oberfläche: ein winziger Ausschnitt dieser Oberfläche ist von einem Ebenenabschnitt so gut wie nicht zu unterscheiden. Das ist exakt analog zu den Eigenschaften der Schwerkraft, die in den letzten beiden Abschnitten behandelt wurden: In einer sehr kleinen Raumzeitregion, der Kabine eines Beobachters etwa, der für eine gewisse Zeit frei fällt, ist von der Schwerkraft fast nichts zu merken. Das Kabineninnere ist von einem Ausschnitt aus der gravitationsfreien Raumzeit der speziellen Relativitätstheorie nicht zu unterscheiden. Erst in einem größeren Raumzeitausschnitt, etwa einer Kabine von riesenhaften Ausmaßen, zeigt sich, dass die betrachtete Raumzeit von der gravitationsfreien, „flachen“ Raumzeit abweicht.
Einstein nahm diese Analogie ernst, und es gelang ihm, tatsächlich eine geometrische Gravitationstheorie auszuarbeiten.
Die Geometrie der Gravitation
In der flachen Raumzeit, der gravitationslosen Raumzeit der Speziellen Relativitätstheorie, bewegen sich Körper, auf die keine äußeren Kräfte wirken, auf „Raumzeitgeraden“: sie laufen mit konstanter Geschwindigkeit entlang gerader Bahnen.
Bringen wir jetzt die Gravitation ins Spiel, etwa indem wir eine massereiche Kugel in unseren Raum setzen. Im Newtonschen Bild der Gravitation übt die Kugel auf sie umgebende kleine Testkörper eine Kraft aus, die diese Testkörper von ihren Raumzeitgeraden ablenkt, indem sie ihre Bahnkurven in Richtung auf die Zentralmasse hin verbiegt und die Testkörper in diese Richtung beschleunigt.
In Einsteins geometrischer Theorie der Gravitation dagegen bewirkt diese Masse eine Verzerrung der Raumzeit: War die gravitationsfreie Raumzeit (jene der speziellen Relativitätstheorie) flach, ist die Raumzeit in Anwesenheit dieser Masse gekrümmt. In dieser gekrümmten Raumzeit gibt es keine Raumzeitgeraden mehr, ebenso wenig wie es auf der Oberfläche einer Kugel Geraden gibt. Es gibt lediglich Geodäten, geradestmögliche Raumzeitbahnen. Testkörper in der Umgebung der Zentralmasse folgen den geradestmöglichen Bahnen in der durch die Masse gekrümmten Raumzeit. Die Gravitation lenkt Testkörper nicht von ihren geraden Bahnen ab – sie verzerrt Raum und Zeit und definiert damit neu, was es bedeutet, sich auf einer geradestmöglichen Bahn zu bewegen.
Einsteins Universum ist damit ein steter Reigen, bei dem Materie und Raumzeit sich gegenseitig beeinflussen: Eine gegebene Materieanordnung verzerrt die Geometrie der Raumzeit; die Geometrie der Raumzeit bestimmt, wie sich die Materie weiterbewegt. Entsprechend der durch die Bewegung leicht veränderten Materiekonfiguration verändert sich auch die Raumzeitgeometrie, diese veränderte Geometrie beeinflusst die weitere Bewegung der Materie nun etwas anders als vorher, und so weiter, und so fort.
Was also ist Gravitation, in Einsteins Universum? Allgemein gesprochen: jede Verzerrung der Geometrie von Raum und Zeit. Genauer betrachtet hat die Gravitation zwei Seiten. Ein Teil der Gravitation ist ein Artefakt, abhängig vom Bezugssystem des jeweiligen Beobachters. Dieser Teil der Gravitation lässt sich zum Verschwinden bringen, wenn man zu einem frei fallenden Bezugssystem übergeht. Was wir hier auf der Erde an Gravitationseffekten beobachten können – im wesentlichen: Körper, die zu Boden fallen – gehört zu dieser Art von „relativer Gravitation“. Der Rest an Gravitation, man könnte ihn „intrinsische Gravitation“ nennen, macht sich durch Gezeitenkräfte bemerkbar und hängt direkt mit einer ganz bestimmten geometrischen Eigenschaft zusammen: der Krümmung der Raumzeit.
Weitere Informationen
Dieses Vertiefungsthema ergänzt die Ausführungen im Kapitel Allgemeine Relativitätstheorie von Einstein für Einsteiger.
Verwandte Vertiefungsthemen finden sich in der Kategorie Allgemeine Relativitätstheorie.
Kolophon
ist Astrophysiker am Max-Planck-Institut für Astronomie, Leiter des Hauses der Astronomie in Heidelberg und Initiator von Einstein Online.
Zitierung
Zu zitieren als:
Markus Pössel, “Gravitation: Vom Fahrstuhl zur Raumzeitkrümmung” in: Einstein Online Band 04 (2010), 02-1118