Extradimensionen auf der Spur
Wie sich zusätzliche Raumdimensionen nachweisen lassen könnten – und warum der Umstand, dass unsere Erde um die Sonne kreist dafür von Bedeutung ist
Ein Artikel von Stefan Theisen
Es ist unmöglich, sich anschaulich vorzustellen, wie die Welt aussähe, besäße sie mehr als die drei Raumdimensionen. Sicher, da gäbe es zusätzliche Raumrichtungen, zu den drei Bewegungsmöglichkeiten vorne-hinten, links-rechts, oben-unten kämen weitere Richtungen hinzu, aber sich das vorzustellen fällt uns dreidimensionalen Wesen außerordentlich schwer. Einfacher ist es, sich zu überlegen, welche Form bestimmte Naturgesetze in solch einer höherdimensionalen Welt haben – und wie sich solch eine Welt in dieser Hinsicht von der unsrigen unterscheidet.
Die Dimensionen des Coulombgesetzes
Ein einfaches Beispiel ist das Coulombgesetz, das bestimmt, wie eine elektrische Ladung Q andere elektrische Ladungen vermittels der so genannten elektrostatischen Kraft anzieht oder abstößt. Die Kraft, die die Ladung Q auf eine andere kleine Ladung q ausübt, die sich im Abstand r von ihr befindet, ist

Genau in derselben Weise wie die Newtonsche Gravitationskraft wird die Coulomb-Kraft bei größerem Abstand der Ladungen immer schwächer.
Für diese Abstandsabhängigkeit gibt es eine einfache Veranschaulichung, die direkt mit der Zahl der Raumdimensionen zusammenhängt. Man kann sich vorstellen, dass von der Ladung Q aus in alle Richtungen „Feldlinien“ zeigen. In einer zweidimensionalen Welt kann man sie sich wie folgt verbildlichen:
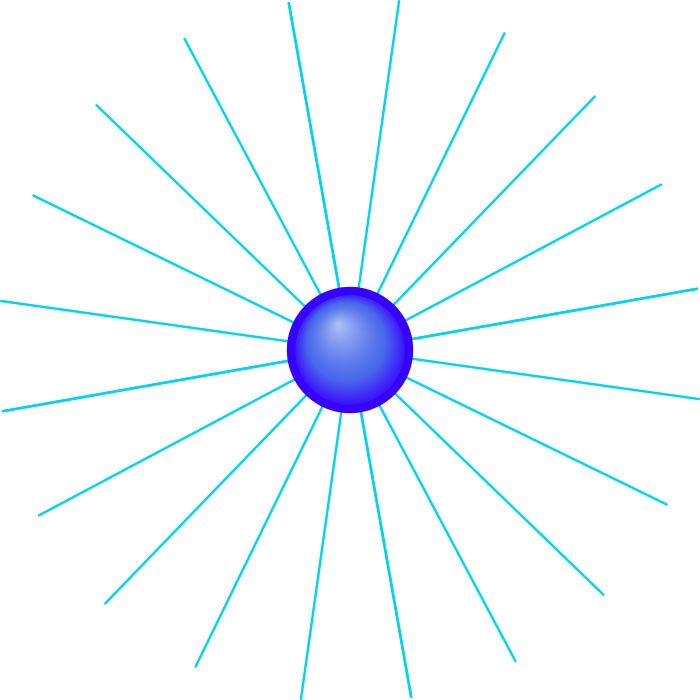
Die Anzahl der Feldlinien ist ein Maß für die Größe der Ladung Q, und ihre Dichte ist ein Maß für die Stärke der Kraft. Das führt direkt auf die Abstandsabhängigkeit der Kraft, denn betrachten wir jetzt beispielsweise zwei Testkörper, von denen der zweite doppelt soweit von der Ladung Q entfernt ist wie der erste (die kleinen roten Kreise links im Bild):
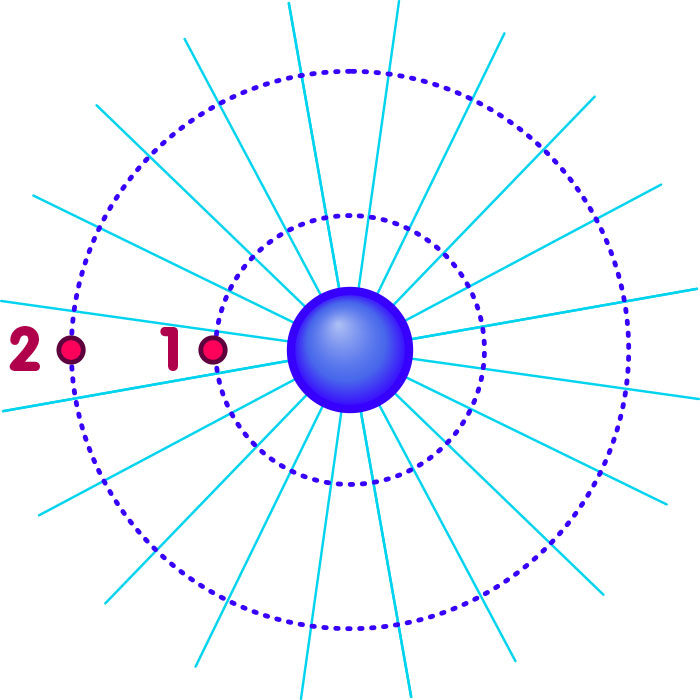
Die Kraftstärke am Ort jedes der Testkörper ist, wie erwähnt, durch die „Dichte der Feldlinien“ gegeben – dadurch, wie viele Feldlinien ein kleines Umfangsstück in unmittelbarer Nähe des jeweiligen Testkörpers durchstoßen. Diese Dichte ist aber proportional zum Abstand: Die Gesamtzahl der Feldlinien ist konstant, und diese Anzahl verteilt sich in jedem Abstand von der Ladung Q auf den gesamten Kreisumfang. In die Abbildung eingezeichnet sind dementsprechend die Kreisumfänge, die zum ersten und zum zweiten Testteilchen gehören. Der Kreisumfang ist nun aber direkt proportional zum Abstand r, und die Dichte der Feldlinien, definiert als ihre Anzahl geteilt durch den Kreisumfang, auf den sie sich verteilen, ist damit proportional zu 1 durch r. Es ist jetzt leicht einzusehen, dass auch die elektrische Kraftstärke proportional zu 1/r sein muss.
Wenn wir jetzt zu drei Dimensionen des Raums übergehen, ist die Argumentation die gleiche: Wieder geht von der zentralen Ladung Q eine konstante Anzahl von Feldlinien aus. Im Abstand r verteilen sie sich nun aber nicht gleichmäßig auf einen Kreisumfang sondern, wir befinden uns in drei Dimensionen, auf eine Kugelfläche, in deren Mittelpunkt die Ladung Q sitzt. Wie viele Feldlinien ein kleines Kugelflächenstück in unmittelbarer Nähe des jeweiligen Testkörpers durchstoßen, ist wiederum ein Maß für die Stärke der Kraft. Allerdings nimmt der Flächeninhalt der Kugel, auf den sich die Feldlinien verteilen, mit dem Quadrat des Abstandes zu. Die Dichte der Feldlinien, gegeben als Anzahl durch Kugelflächeninhalt, nimmt damit umgekehrt mit eins durch das Quadrat des Radius ab. Genau wie diese Dichte nimmt auch die Stärke der Kraft mit dem Abstand ab, entsprechend dem Faktor eins durch r2 in der eingangs erwähnten Formel.
Drei und noch mehr Dimensionen
Es ist einfach, das Argument auf D Raumdimensionen zu verallgemeinern – mit Feldlinien, höherdimensionalen Entsprechungen von Kreis und Kugelfläche, und mit dem allgemeinen Ergebnis: Die Stärke der Coulomb-Kraft ist proportional zu eins durch r(D-1).
Solche Überlegungen über die Anzahl der Dimensionen des Raumes sind durchaus nicht erst mit der modernen Physik aufgekommen. Schon Immanuel Kant hat in seiner ersten Schrift „Gedanken von der wahren Schätzung der lebendigen Kräfte“ (1749) darauf hingewiesen, dass die Abstandsabhängigkeit des Newtonschen Gravitationsgesetzes die Dreidimensionalität des Universums widerspiegelt. Gleichzeitig hat er darüber spekuliert, dass es parallele Universen mit einer anderen Anzahl von Dimensionen geben könnte. In heutiger Zeit ist die Dimensionsabhängigkeit von Kräften interessant, da Theorien wie die Stringtheorie tatsächlich postulieren, unsere Welt habe mehr als drei Raumdimensionen.
Das Coulombsche Gesetz ist nun sehr genau experimentell überprüft worden und es konnten bisher keinerlei Abweichungen gemessen werden. Wenn unsere Welt Extra-Dimensionen hat, müssen sie daher gut versteckt sein. Dazu gibt es im Wesentlichen zwei Möglichkeiten. Entweder, die zusätzlichen Dimensionen sind sehr klein „aufgerollt“ – was das zu bedeuten hat, ist Inhalt des Vertiefungsthemas Extradimensionen – und wie man sie versteckt. Für aufgerollte Dimensionen, so lässt sich zeigen, sieht das Kraftgesetz aus wie im dreidimensionalen Raum – es sei denn, man misst es bei sehr, sehr kleinen Abständen, viel kleiner als der heutigen Überprüfung zugänglich. Oder aber, unsere Welt ist in die höheren Dimensionen eingebettet, ähnlich, wie ein Blatt Papier ein Ausschnitt aus einer zweidimensionalen Fläche ist, eingebettet in den dreidimensionalen Raum. Das ist Inhalt des Vertiefungsthemas Die eingebettete Welt.
Weitere Informationen
Die relativistischen Grundkonzepte, die diesem Vertiefungsthema zugrundeliegen, werden in Einstein für Einsteiger erklärt, insbesondere auf der Seite Superfäden und universelle Harmonie des Kapitels Relativität und Quanten.
Mehr zu den Extradimensionen bieten die Vertiefungsthemen Eine Frage der Sichtweise, Extradimensionen – und wie man sie versteckt und Die eingebettete Welt. Verwandte Vertiefungsthemen auf einstein-online finden sich in der Kategorie Relativität und Quanten.
Kolophon
ist Wissenschaftler und Forschungsgruppenleiter am Albert-Einstein-Institut. Sein Forschungsgebiet ist die Stringtheorie.
Zitierung
Zu zitieren als:
Stefan Theisen, “Extradimensionen auf der Spur” in: Einstein Online Band 04 (2010), 01-1128










