Hunting for extra dimensions
Ways of detecting extra dimensions – and why the fact that our earth orbits the sun is a relevant data point
An article by Stefan Theisen
It is impossible to picture how a world with more than three space dimensions would look like. There would be additional spatial directions, complementing the well-known threesome of up-down, left-right, forward-backward. But when it comes to picturing these directions, we are faced with insurmountable difficultires, dwellers in three dimensions as we are. It is simpler to address another questions: how would the laws of physics in such a higher-dimensional world – and how would they differ from the three-dimensional laws we are used to?
The dimensions of Coulomb’s law
A simple example is Coulomb’s law, which describes the strength of the electrostatic force with which a particle carrying the electric charge Q attracts other charged particles – or repels them. The strength of the force by which a charge Q acts on a charge q if the distance between them is r is given by

Coulomb’s force decreases as the distance between the charges increases – in exactly the same way as the gravitational force in Newtonian gravity.
For this dependence on distance, there is a simple picture that is intimately connected with the number of spatial dimensions. One can imagine that, from Q, “field lines” run in all directions. In a two-dimensional world, this would lead to the following picture:
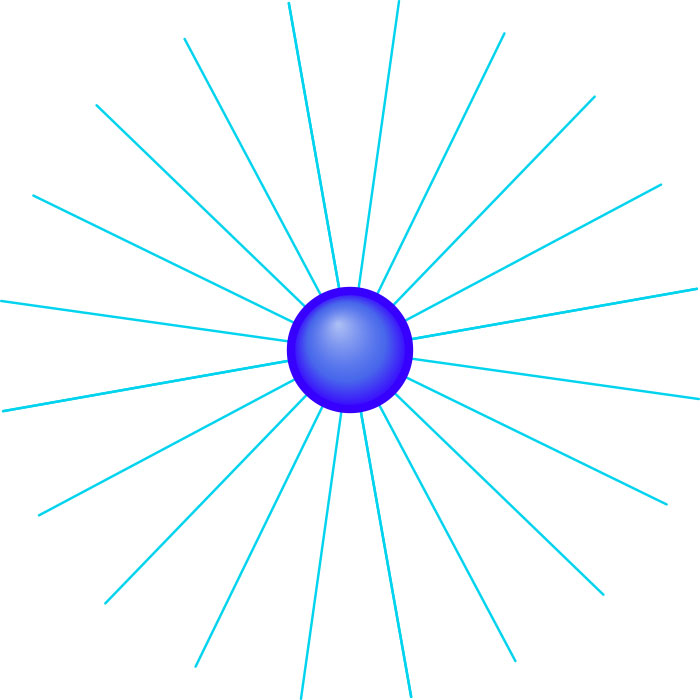
The number of field lines is a measure for the size of the charge Q; their density (how many field lines in a given volume of space?) a measure for the strength of the force. Now, look at two test particles, where the distance of the second test particle from the charge is twice as large as for the first (corresponding to the two little red circles on the left):
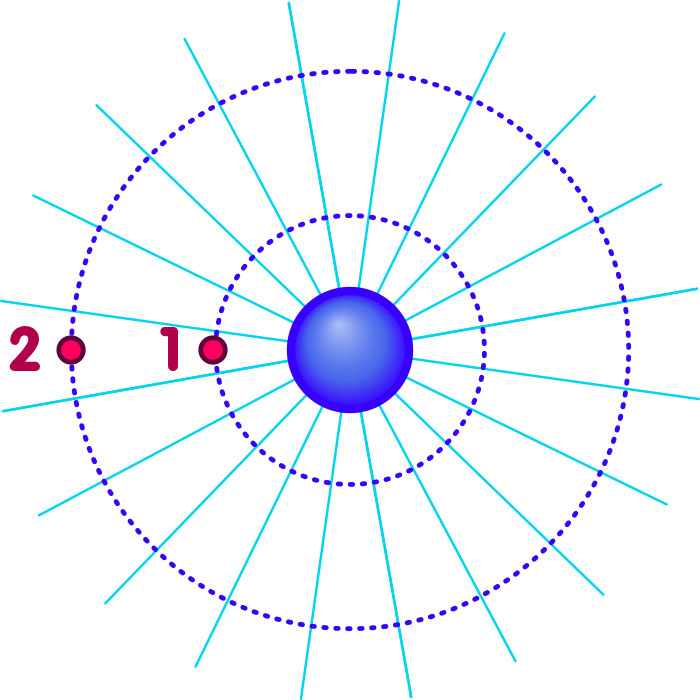
As was already mentioned, the strength of the force at the location of each of the test particles is given by the “density of the field lines” – the number of field lines traversing a small segment of the circumference in the direct vicinity of the test particle in question. This density is directly proportional to the inverse of the distance: The total number of field lines originating at Q is constant, and this number is spread out around the whole circle of possible test particle locations at a certain distance from Q. Two such circles are given in the figure above, corresponding to the location of the first and the second test particle. The circumference of the circle is directly proportional to the radius r, and the density of the field lines, defined as their number divided by the circumference over which they are spread, is thus proportional to one over r. Consequently, the strength of the force also varies with distance as one over r.
Three and more dimensions
In three dimensions, one can argue in exactly the same way: Again, a constant number of field lines originates at Q. However, at the distance r, those field lines are spread out not over the circumference of a circle – we are in three dimensions, and all points at distance r correspond to the surface of a sphere with Q as the centre point. Again, the field line density, in this case: the number of field lines crossing a tiny section of the surface is a measure for the strength of the force. However, in three dimensions the surface area of a sphere increases with the square of the radius. If the area over which the field lines are spread increases with the square of the distancen, then the field line density is proportional to one over the square of the distance. This density is a measure for the strength of the force, and so this force, too, decreases as one over the square of the distance – corresponding to the factor one over r2 in the formula given in the beginning.
The argument is readily generalized to D dimensions – with field lines, higher-dimensional analogues of circle and spherical surface, and with the general result: The strength of the Coulomb force is proportional to one over r(D-1).
Arguments like this are not new – they go back at least to the 18th century, when the philosopher Immanuel Kant, in his first publication, “Thoughts about the true estimation of the living forces” (1749) pointed out how Newton’s law of gravity reflects the fact that our universe is three-dimensional. In modern times, the dimension-dependence of forces is of interest in the context of models such as those of string theory, in which space has indeed more than three space dimensions.
Coulomb’s law has been subject to rigorous experimental tests, and so far, no deviations from the inverse square law have been found. If there are extra space dimensions, they must be well hidden. There are basically two ways to hide dimensions. Either, the additional dimensions are “rolled up” – details about what this means can be found in the spotlight topic Extra dimensions – and how to hide them. It can be shown that, for rolled-up extra dimensions, Coulomb’s law is the same as in ordinary, three-dimensional space, except at very, very small distances – distances much smaller than can be probed experimentally in the foreseeable future. The other possibility is that our world is embedded in higher dimensions, analogous to a piece of paper, a two-dimensional region, being embedded in three-dimensional space. More information about this can be found in the spotlight topic The embedded universe.
Further Information
The relativistic background of this spotlight topic is explained in Elementary Einstein, especially on the page Superstrings and universal harmony in the chapter Relativity and the quantum.
For more information about extra dimensions, check out the spotlight topics Extra dimensions – and how to hide them, The embedded universe and Simplicity in higher dimensions. Related spotlight topics can be found in the section Relativity and the quantum.
Colophon
is a research group leader at Albert Einstein Institute with a research focus on string theory.
Citation
Cite this article as:
Stefan Theisen, “Hunting for extra dimensions” in: Einstein Online Band 04 (2010), 01-1027










