Gleichgewicht und Veränderung
Informationen zu dem Wettstreit zwischen thermodynamischem Gleichgewicht und Expansion, der die Elementhäufigkeiten im frühen Universum bestimmt
Ein Artikel von Achim Weiss
Untersuchungen zur primordialen Nukleosynthese – der Entstehung verschiedener Arten leichter Atomkerne, etwa der Elemente Helium, Deuterium und Lithium, im frühen Universum – führen zu einigen der beeindruckendsten Vorhersagen der Urknallmodelle. Einen kurzen Überblick bietet das Vertiefungsthema Elemententstehung im frühen Universum. In diesem Text geht es um die Physik hinter den Vorhersagen.
Veränderliches Gleichgewicht
Lassen wir die frühesten Phasen beiseite – über sie kann die moderne Physik nach wie vor nur sehr unsichere Aussagen treffen -, dann war das wenige Sekundenbruchteile alte Universum mit einem heißen Plasma aus Strahlung und Elementarteilchen angefüllt. All die verschiedenen Bestandteile befanden sich im thermodynamischen Gleichgewicht.
Bei einem System im thermodynamischen Gleichgewicht ist die Energie per Definition gleichmäßig auf alle Bestandteile verteilt. Für ein einfaches Gas beispielsweise haben all die unzähligen, wild durcheinanderfliegenden Gasteilchen im Mittel die gleiche Bewegungsenergie. Für Systeme wie den Materieinhalt des frühen Universums kommt freilich noch ein weiterer Aspekt hinzu: Dort sind die Teilchen in stetigem Wandel begriffen – andauernd finden Reaktionen statt, bei denen Teilchen einer Spezies in Teilchen einer anderen Spezies umgewandelt werden.
Für solch ein System geht thermisches Gleichgewicht bei einer gegebenen Temperatur zwingend mit bestimmten relativen Häufigkeiten der verschiedenen Teilchenarten einher – wieviele Teilchen einer bestimmten Art B auf jedes Teilchen einer anderen Art A kommen, ist im Gleichgewicht eindeutig festgelegt. Die genauen Häufigkeitswerte hängen dabei von der Temperatur ab: Während sich die Temperatur des frühen Universums ändert, ändert sich auch das Teilchengemisch.
Vom Nebel zu den Elementarteilchen
Veränderliche Gleichgewichte dieser Art spielen bei weitem nicht nicht nur im frühen Universum eine Rolle. Ein alltagsnäheres Beispiel ist die Luft an einem kühlen Herbstabend, in der das Wasser zum Teil gasförmig, das heißt als Wasserdampf, und zum Teil in Form winziger Tröpfchen vorliegt, nämlich als Nebel. Das System aus diesen beiden „Materiearten“ befindet sich in einem (von der Temperatur und vom Druck abhängigen) Gleichgewicht. Wasser im gasförmigen wird dabei andauernd in Wasser im flüssigen Zustand umgewandelt, und umgekehrt: Bei genauem Hinsehen werden wir überall auf Tröpfchen stoßen, die gerade am Verdampfen sind, und auf Dampf, der gerade zu Tröpfchen kondensiert:
Das Gleichgewicht, das sich bei diesen Reaktionen einstellt – wieviel Wasser in jeder Raumregion liegt in Form von Tröpfchen vor, wieviel als Dampf? – hängt von der Temperatur ab. Wenn wir uns jetzt vorstellen, die Temperatur sinke, während der Abend allmählich zur Nacht wird, dann nimmt die Kondensationsrate zu. Damit liegt mehr und mehr Wasser in Form von Tröpfchen vor, und der Nebel wird dichter. Bleibt die Temperatur anschließend konstant, so bleibt auch die Dichte des Nebels unverändert. Am Morgen dagegen, wenn die Temperatur wieder ansteigt, gewinnt die Verdampfung die Oberhand, und die Luft wird zunehmend klarer während immer mehr der Tröpfchen verdampfen – bis schließlich gar keine Tröpfchen mehr vorhanden sind.
Das Gleichgewichts-Mengenverhältnis zwischen Wasserdampf und Nebeltröpfchen lässt sich mit Hilfe einfacher statistischer Formeln angeben. Die Hauptrollen darin spielen eine Art „Potential“ (in guter Näherung die Energie, die aufgewendet werden muss, um Wassertröpfchen in Dampf zu verwandeln – die Bindungsenergie) und ein Kontrollparameter, die Temperatur oder, äquivalent dazu, die Wärmeenergie. Genauer gesagt ist die entscheidende Größe das Verhältnis von Bindungsenergie und mittlerer Wärmeenergie.
Die Zusammensetzung der Materie im frühen Universum, die sich ebenfalls im thermischen Gleichgewicht befand, gehorcht exakt denselben Formeln. An ihnen lässt sich ablesen, wie sich das Materiegemisch mit abnehmender Temperatur veränderte. Auch hier spielt das Verhältnis von Bindungsenergien zu mittlerer Wärmeenergie die entscheidende Rolle, wenn es darum geht, den Anteil jeder Teilchenspezies an der Gesamtzahl aller Teilchen festzulegen.
Weltall im Gleichgewicht
Zeichnen wir die Entwicklung des frühen Universums zwischen rund einer hundertstel Sekunde und drei Minuten kosmischer Zeit nach. Zu Beginn dieses Zeitraums war das Universum mit einem Plasma gefüllt, dessen Bestandteile heutigen Physikern wohlbekannt sind: Protonen und Neutronen in etwa zu gleichen Teilen als Vertreter dessen, was Physiker baryonische Materie nennen, außerdem Elektronen und ihre Antiteilchen (Positronen), sowie Neutrinos und Photonen. Im Mittel entfiel auf jedes dieser Myriaden von Teilchen die gleiche Menge an Energie. Ähnlich wie beim Nebelbeispiel ständig Tröpchen verdampften oder sich aus Wasserdampf neue Tröpfchen bildeten, war das Gleichgewicht auch hier mitnichten statisch – ständig kam es zu Teilchenreaktionen in denen Teilchen zerfielen oder sich zu andersartigen Teilchen zusammenfanden. Im Durchschnitt blieb die Anzahl der Teilchen jeder der Spezies dabei freilich gleich.
In dieser speziellen kosmischen Entwicklungsphase waren die wichtigsten Kräfte die elektromagnetische Wechselwirkung und die so genannte schwache Kernkraft (die bestimmte radioaktive Zerfälle bewirkt). Diese beiden Kräfte waren für eine Vielfalt verschiedener Reaktionen verantwortlich. Beispielsweise wandelten sich Protonen immer wieder über die schwache Kernkraft in Neutronen um, und umgekehrt – die entsprechenden Reaktionen sind in den nachfolgenden Abbildungen skizziert. In dieser Reaktion treffen ein Proton und ein Elektron zusammen; dabei entstehen ein Neutron und ein so genanntes Elektron-Neutrino (ein fast masseloses Teilchen ohne elektrische Ladung):

Umgekehrt kann sich ein Neutron zusammen mit einem Positron in ein Proton plus das Antiteilchen eines Elektron-Neutrinos verwandeln:

Berücksichtigt man all diese Reaktionen und bemüht die statistischen Gleichungen für das thermische Gleichgewicht, dann ist das Ergebnis eindeutig und recht einfach: In dieser Phase des frühen Universums gab es in etwa genauso viele Protonen wie Neutronen.
Das Wettrennen zwischen Gleichgewicht und Veränderung
So weit, so gut – allerdings kommt noch ein weiterer Umstand hinzu: Ändern sich die äußeren Bedingungen für ein System, so dauert es eine gewisse Zeit, bis sich der neue Gleichgewichtszustand eingestellt hat. In der Entwicklung des frühen Universums spielt diese Trägheit, mit der das System auf Veränderungen reagiert, eine wichtige Rolle.
Die Zeit, die benötigt wird, damit sich ein Gleichgewicht einstellt, hängt direkt davon ab, wie eng die einzelnen Komponenten des Systems miteinander in Kontakt stehen. Das ist nicht überraschend – thermisches Gleichgewicht ist genau dann erreicht, wenn die vorhandene Energie gleichmäßig über das ganze System verteilt ist, so dass auf jede Komponente im Mittel der gleiche Energiebetrag entfällt. Ändern sich die äußeren Bedingungen, dann wird es in der Regel nötig sein, Energie zwischen den einzelnen Komponenten umzuverteilen. Tritt jedes Teilchen in der Sekunde mit Millionen anderer Teilchen in Wechselwirkung, dann wird die Umverteilung recht schnell vonstatten gehen. Trifft jedes Teilchen dagegen nur sehr selten auf ein anderes, dann wird es auch entsprechend lange dauern, bis das Gleichgewicht erreicht ist.
Wie häufig es zu einer bestimmten Art von Reaktion kommt, hängt unter anderem von der Energie der Teilchen und von der Teilchendichte ab. Verändern sich die äußeren Bedingungen, dann werden sich im allgemeinen auch die Reaktionsraten ändern. In Extremfällen können Teilchenreaktionen eines bestimmten Typs so selten werden, dass sie keinen merklichen Beitrag mehr leisten – man spricht davon, es komme zu einem „Ausfrieren“ dieser Teilchenreaktionen. Von diesem Zeitpunkt an bleiben die entsprechenden Teilchenhäufigkeiten unverändert, selbst dann, wenn sie mit der Zeit deutlich von den Gleichgewichtswerten abweichen.
Damit hängen die Auswirkungen veränderlicher äußerer Bedingungen ganz entscheidend von zwei Zeitskalen ab: Verändern sich die äußeren Bedingungen im Vergleich mit der Zeit, die das System benötigt, um sich den neuen Bedingungen anzupassen, nur sehr langsam, dann wird sich das System während des Änderungsprozesses zu jedem Zeitpunkt in einem Gleichgewichtszustand befinden. Ändern sich die äußeren Bedingungen dagegen zu rasch, dann kann sich das System nicht schnell genug anpassen – zu jedem Zeitpunkt der Entwicklung befindet es sich in einem Nicht-Gleichgewichtszustand, immer auf dem Weg zu dem den aktuellen äußeren Bedingungen entsprechenden Gleichgewicht, aber im Vergleich mit den sich ändernden äußeren Umständen immer zu langsam.
Im frühen Kosmos waren die äußeren Umstände in steter Veränderung begriffen – während das Weltall expandierte, kühlte es sich immer weiter ab. Das Teilchengemisch zu jedem Zeitpunkt hing daher von dem Wettrennen zwischen denjenigen Reaktionen ab, die nötig sind, um das temperaturabhängige Gleichgewicht herbeizuführen, und den Temperaturänderungen infolge der kosmischen Expansion.
Das Ausfrieren der schwachen Wechselwirkung
Bis etwa eine Zehntel Sekunde kosmischer Zeit liefen die Neutronen und Protonen betreffenden Reaktionen der schwachen Kernkraft schnell genug ab, dass sich diese Teilchenarten zu jedem Zeitpunkt im Gleichgewicht befanden. Danach freilich, als die Temperatur auf unter hundert Milliarden Kelvin gefallen war (entsprechend einer mittleren Energie von 10 MeV pro Teilchen), änderte sich die Lage: Bei solchen Temperaturen sind die Reaktionsraten für schwache Wechselwirkungen zwischen Neutrinos und dem elektromagnetischen Feld so gering, dass diese zwei Arten von Materie sich voneinander „entkoppeln“ und nun so gut wie gar nicht mehr miteinander wechselwirken. Außerdem kam es zu Vernichtungsreaktionen zwischen den allermeisten Elektronen und Positronen, während die elektromagnetische Strahlung nun andererseits zu weit abgekühlt war, als dass sie neue Elektron-Positron-Paare hätte hervorbringen können. Als Folge erhöhte sich die Temperatur des Strahlungsfeldes (nicht aber die der Neutrinos, die sich bereits von der Entwicklung des restlichen Universums abgekoppelt hatten). Da es ein winziges bisschen mehr Elektronen als Positronen gegeben hatte, blieben auch nach den Vernichtungsreaktionen einige wenige Elektronen übrig – dies sind all die Elektronen, die wir auch heute noch im Universum vorfinden.
Zu Beginn der neuen Ära kamen auf jedes Neutron im Schnitt sechs Protonen. Das entspricht ungefähr dem Gleichgewichtsverhältnis unter den entsprechenden Temperaturbedingungen. Allerdings ließ sich das Gleichgewicht nicht aufrecht erhalten. Dazu hätte es häufiger schwacher Kernreaktionen bedurft wie jener, die oben beschrieben wurden. Tatsächlich aber gab es zu jener Zeit nur noch sehr wenige Elektronen und kaum Positronen, so dass sich kaum noch schwache Reaktionen ereigneten. Aufgrund der Expansion veränderte sich der Kosmos deutlich zu schnell, als dass diese seltenen schwachen Kernreaktionen mit der Entwicklung Schritt halten und jeweils den entsprechenden Gleichgewichtszustand hätten herstellen können. Es kam zu genau solch einem Wettrennen zwischen Gleichgewicht und Veränderung, wie ich es oben bereits beschrieben habe – und das Resultat war eindeutig: Es kam zum Ausfrieren der schwachen Wechselwirkung.
Die einzigen schwachen Reaktionen, die nach wie vor von praktischer Bedeutung blieben, war der Zerfall von Neutronen in die etwas leichteren Protonen. Dessen Eigenschaften hängen nicht von der Temperatur ab, und der Zerfall ereignet sich mit einer Halbwertszeit von 889 Sekunden – beobachtet man ein Ensemble freier Neutronen über diesen Zeitraum hinweg, dann wird am Ende im Mittel die Hälfte davon zerfallen sein.
Die Entstehung der leichten Atomkerne
An dieser Stelle war von entscheidender Wichtigkeit, wie schnell das Universum expandierte. Hätte es sich nur ein wenig schneller ausgedehnt, dann wären im Laufe von etwa einer Stunde so gut wie alle Neutronen zerfallen, und übrig geblieben wäre ein ausschließlich mit Protonen (also Wasserstoffkernen) gefüllter Kosmos. Glücklicherweise verliefen die Expansion und, damit einhergehend, die Abkühlung langsamer, so dass genügend Zeit blieb für Reaktionen, bei denen Neutronen und Protonen sich zu verschiedenen Arten von Atomkernen verbanden. Das Universum trat in das Stadium der primordialen Nukleosynthese ein, wobei „primordial“ das Adjektiv für alles ist, was die Frühzeit des Kosmos betrifft, „Nukleosynthese“ der Fachausdruck für die Entstehung zusammengesetzter Atomkerne.
Wieviele Atomkerne der verschiedenen möglichen Sorten bildeten sich dabei? Diese Frage wird einmal mehr entschieden im Zusammenspiel von Reaktionszeiten, Gleichgewicht und kosmischer Expansion. Und wieder muss man eine ganze Reihe verschiedener Reaktionen in die Rechnung einbeziehen. So können sich Proton und Neutron zu einem Deuterium-Kern verbinden (Deuterium ist die schwere Variante des Wasserstoffs), und auf dieser Basis kann durch Hinzufügen entweder eines Protons oder eines Neutrons ein Atomkern von Helium-3 (einer leichten Variante des Heliums) oder Tritium (superschwerer Wasserstoff) entstehen.
Zu Beginn der Nukleosynthese, bei einer kosmischen Zeit von etwa einer Sekunde, war die Lage noch vergleichsweise übersichtlich. Die Kernreaktionen fanden rasch genug statt, um ein Gleichgewicht herzustellen, in dem bevorzugt leichte Elemente wie Wasserstoff, Helium und ihre Isotope Deuterium (d), Tritium (t) und Helium-3 vorkommen. Die Temperatur des Plasmas aus Strahlung und Materie betrug zu jenem Zeitpunkt rund zehn Milliarden Kelvin. Bei dieser Temperatur entfällt auf jedes der vorhandenen Teilchen im Mittel eine Energie von rund 1 MeV. Die Kernphysik unter solchen Bedingungen, und insbesondere die verschiedenen Reaktionsraten, sind gut erforscht. Solche Energien lassen sich ohne großen Aufwand in Laborexperimenten mit Atomkernen erreichen.
Bis zu einer kosmischen Zeit von etwa einer Minute blieb die Situation weitgehend unverändert. Neutronen und Protonen gab es im Zahlenverhältnis von etwa 1:7 (auf ein Neutron kamen je sieben Protonen – und es war bei weitem noch nicht genügend Zeit vergangen, dass der allmähliche radioaktive Zerfall von immer mehr Neutronen in Protonen eine Rolle gespielt hätte). Könnten wir die Expansion des Universums zu diesem Zeitpunkt anhalten, lange genug, dass die schwachen Kernreaktionen das durch sie vermittelte Gleichgewicht herstellen könnten, dann würde das Zahlenverhältnis auf ein Neutron für je 74 Protonen abfallen. Stattdessen nimmt die Expansion ihren Lauf, und die Temperatur sinkt in den nachfolgenden zwei bis drei Minuten von rund 3 bis auf rund eine Milliarde Kelvin (von 0,3 bis auf 0,1 MeV Energie pro Teilchen).
Die Expansion verläuft allmählich genug, dass eine andere Art von schneller Reaktion wichtig wird – das Einfangen von freien Neutronen durch Protonen oder leichte Atomkerne. Durch solche Einfangprozesse können immer schwerere Atomkerne entstehen, wie hier skizziert:
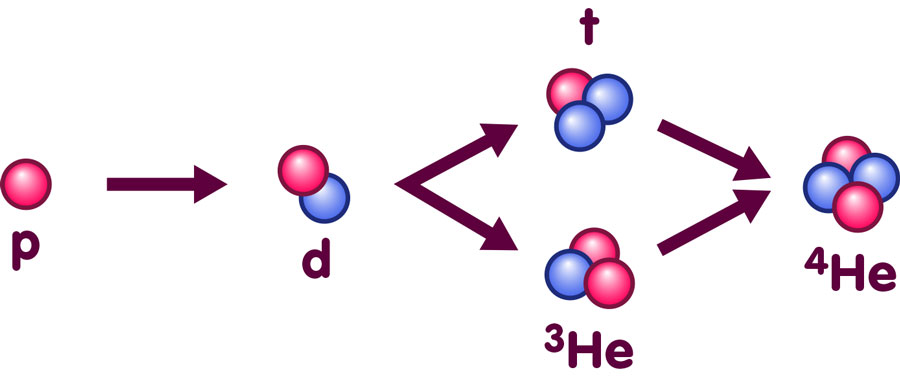
Tatsächlich sind die Protonen und Neutronen bei dem Isotop Helium-4, oder 4He, stärker aneinander gebunden als in jedem anderen Atomkern (weitere Informationen zur Bindungsenergie liefert das Vertiefungsthema Ist das Ganze die Summe seiner Teile?). Bei niedrigeren Temperaturen ist diese Konfiguration von Protonen und Neutronen daher ein besonders bevorzugter Zustand – würden wir die kosmische Expansion an diesem Zeitpunkt anhalten und abwarten, dann erhielten wir ein Universum, das fast nur Helium-4-Kerne enthält. Sogar die Protonen hätten sich dann zusammengefunden und einige davon hätten sich in Neutronen umgewandelt, um Helium-4-Kerne aus je zwei Neutronen und zwei Protonen zu bilden.
Tatsächlich aber verläuft die kosmische Expansion im Vergleich mit der Zeitskala für die Umwandlung von Protonen in Neutronen vergleichsweise schnell. Einmal mehr gelingt es der Materie nicht, einen Gleichgewichtszustand zu erreichen, und einmal mehr hängt das Ergebnis von einem Wettrennen zwischen Kernreaktionen und Expansion ab.
Es ist recht einfach, abzuschätzen, wie das Rennen ausgeht. Vergleicht man die verschiedenen Zeitskalen, dann zeigt sich, dass kaum ein Proton die Zeit gehabt haben wird, sich einem der bereits existierenden Atomkerne anzuschließen und sich dann in ein Neutron umzuwandeln. Dagegen sind die Reaktionen, bei denen sich bereits existierende Neutronen mit Protonen zu Atomkernen zusammenfinden schnell genug, dass sich alle Helium-4-Kerne, die auf diese Weise entstehen können, auch tatsächlich bilden. Letztes Puzzlestück ist das bereits erwähnte Zahlenverhältnis von Neutronen und Protonen von eins zu sieben zu Beginn der Nukleosynthese.
Sind all diese Informationen gegeben, fällt die Abschätzung leicht. Betrachten wir 16 Nukleonen, von denen zwei Neutronen und 14 Protonen sind (das ist gerade das vorherrschende fast-Gleichgewichtsverhältnis von eins zu sieben). Aus diesen Nukleonen kann ohne die Umwandlung von Protonen und Neutronen gerade ein einziger Helium-4-Kern entstehen, denn für jeden solchen Kern benötigen wir zwei Neutronen und zwei Protonen. Übrig bleiben 12 Protonen oder, anders ausgedrückt, 12 Wasserstoff-Atomkerne. Das Massenverhältnis von Helium-4 zu Wasserstoff ist damit 4/12, oder anders gesagt: Von der Gesamtmasse der Atomkerne im frühen Universum entfallen 75 Prozent auf Wasserstoffkerne, 25 Prozent auf Helium-4-Kerne. Eine direkte und robuste Vorhersage, die nichts voraussetzt als die Zeitskalen der kosmischen Expansion und einige einfache Physik des thermodynamischen Gleichgewichts bei wohlerforschten Temperaturen.
Bei näherem Hinsehen ist dieses Bild freilich zu vereinfacht. Genaueren Berechnungen der relativen Häufigkeiten der verschiedenen Arten von Atomkernen im frühen Universum liegt ein ganzes Netzwerk von Kernreaktionen zugrunde. Die wichtigsten davon sind hier skizziert:
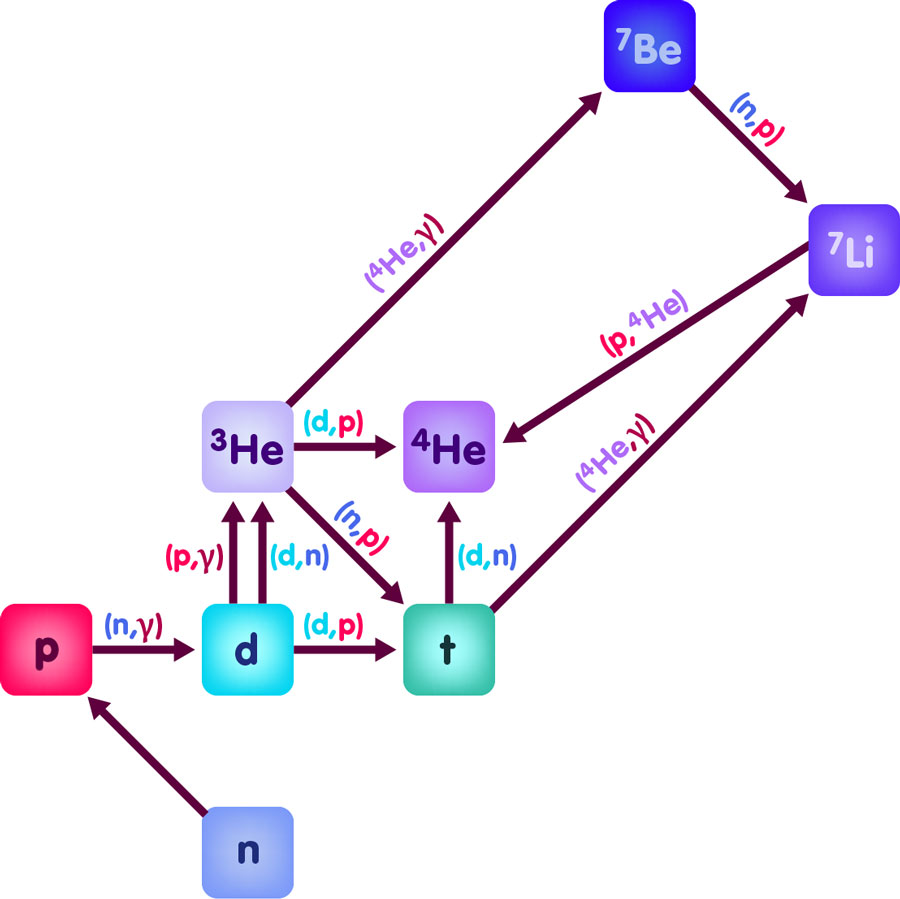
In diesem Diagramm zeigt die Höhe eines Kerns über der Grundlinie die Zahl der in ihm enthaltenen Protonen an, sein Abstand vom linken Rand die Anzahl seiner Neutronen. Die verschiedenen Reaktionen sind durch Pfeile dargestellt, die von einer Art von Atomkern zu einer anderen Zeigen. Die Beschriftung der Pfeile gibt Auskunft über den Verlauf der Reaktion. Beispielsweise steht an dem Pfeil zwischen Deuterium (d) und Tritium (t) eine Beschriftung (d,p), die anzeigt, dass wir, um einen Deuteriumkern in einen Tritiumkern umzuwandeln, einen weiteren Deuteriumkern d hinzufügen müssen, und dass am Ende nicht nur das Tritium, sondern noch ein überzähliges Proton p herauskommt. Analog müssen wir, um von Deuterium zu Helium-3 zu gelangen, ein Proton p hinzufügen, und heraus kommt dabei nicht nur Helium-3, sondern auch ein Photon. Photonen werden üblicherweise mit dem griechischen Buchstaben Gamma bezeichnet; dementsprechend trägt der Pfeil, der von Deuterium zu Helium-3 zeigt, die Beischrift (p,γ). Alternativ könnte man dem Deuterium auch einen zweiten Deuteriumkern hinzufügen; dabei würde ein zusätzliches Neutron freigesetzt.
In der obigen Abbildung sind zwölf Kernreaktionen dargestellt. In den eigentlichen Rechnungen werden noch andere Isotope des Lithium sowie noch schwerere Elemente mit einbezogen, und es werden insgesamt über vierzig verschiedene Reaktionen berücksichtigt – all das vor dem Hintergrund eines expandierenden Universums, in dem die meiste Energie in Form von elektromagnetischer Strahlung vorliegt. Die meisten Parameter, die in die Rechnung eingehen, etwa die Reaktionsraten und das ursprüngliche Zahlenverhältnis von Protonen zu Neutronen sind wohlbekannt – bis auf einen: die Gesamtdichte der baryonischen Materie, mit anderen Worten: Wieviele Protonen und Neutronen enthält eine gegebene Region des Kosmos?
Dieser Dichteparameter hat einen direkten Einfluss auf die Ergebnisse: Ist die Dichte höher, dann kommt es allgemein häufiger zu Kernreaktionen. Die Entstehung von Helium-4 über die Zwischenstufen Deuterium und Helium-3 geht schneller voran, und die freien Neutronen haben weniger Zeit, radioaktiv zu Protonen zu zerfallen. Insgesamt entstehen so mehr Helium-4-, aber weniger Deuterium- und Helium-3-Kerne.
Dieser Schluss lässt sich auch umkehren. Sind die Häufigkeiten der leichten Elemente im frühen Universum aus Beobachtungen bekannt, und passen sie zu den Vorhersagen zur primordialen Nukleosynthese für einen ganz bestimmten Wert der Proton/Neutron-Dichte, dann dürften die Dichte der Baryonen (Protonen plus Neutronen) im frühen Universum eben diesen Wert gehabt haben.
Wie sich die Elementhäufigkeiten während der Elementenstehungsphase kurz nach dem Urknall mit der Zeit entwickeln, zeigt das folgende Diagramm. Für die Baryonendichte wurde dabei ein Wert von einem Baryon für je 3 Milliarden Photonen der kosmischen Hintergrundstrahlung zugrundegelegt:
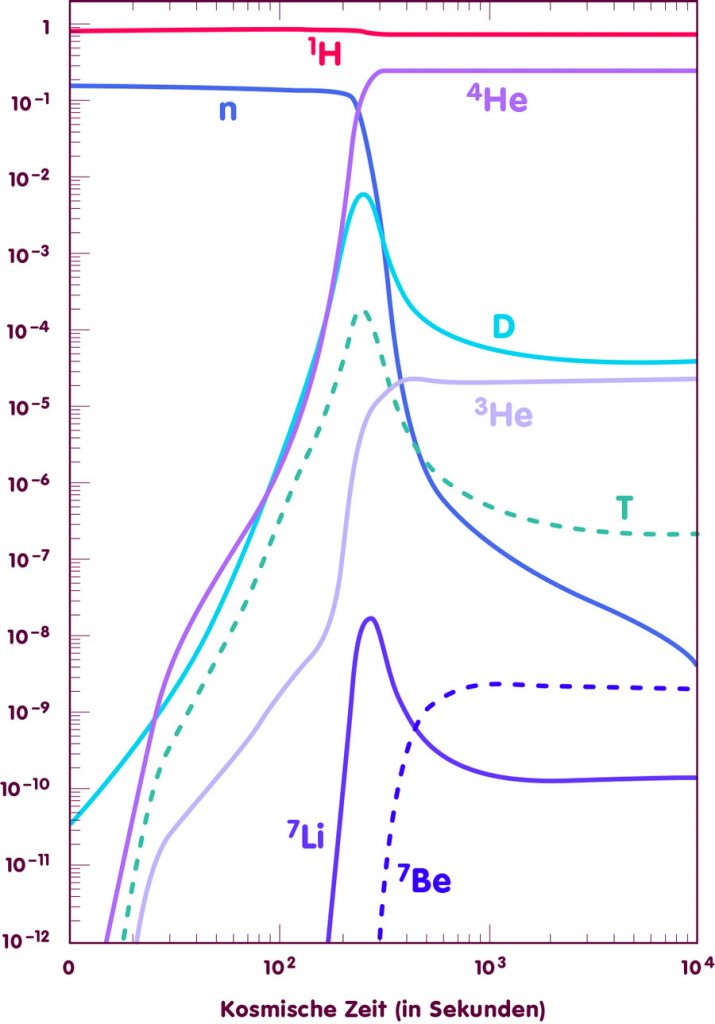
[Nach einer Grafik von E. Vangioni, Institut d’Astrophysique de Paris]
Die Rechnungen zur Entstehung der leichten Elemente liefern einige der erfolgreichsten Vorhersagen der Urknallmodelle: Die Physik im expandierenden Universum im Zeitraum von einer bis drei Minuten kosmischer Zeit ist gut erforscht und vergleichsweise einfach. Dementsprechend sind die Vorhersagen zu den Elementhäufigkeiten eindeutig und robust. Dabei besteht eine gute Übereinstimmung zwischen den Vorhersagen und den aus Beobachtungen erschlossenen Elementhäufigkeiten im frühen Universum – ein gewichtiges Indiz dafür, dass die Urknallmodelle diese Phase unserer kosmischen Geschichte zutreffend beschreiben.
Weitere Informationen
Die relativistischen Grundkonzepte, die diesem Vertiefungsthema zugrundeliegen, werden in Einstein für Einsteiger erklärt, insbesondere im Abschnitt Kosmologie.
Einen Überblick über die primordiale Nukleosynthese bietet das Vertiefungsthema Elemententstehung im frühen Universum; Informationen zum Vergleich von Vorhersagen und Beobachtungen das Thema Der Blick in die chemische Vergangenheit. Verwandte Vertiefungsthemen auf Einstein-Online finden sich in der Kategorie Kosmologie.
Kolophon
ist Wissenschaftler am Max-Planck-Institut für Astrophysik in Garching bei München, wo er sich mit der Physik der Sterne beschäftigt.
Zitierung
Zu zitieren als:
Achim Weiss, “Gleichgewicht und Veränderung” in: Einstein Online Band 02 (2006), 02-1112