Auf allen möglichen Wegen zum Ziel
Zu den so genannten Pfadintegralen, einem wichtigen Konzept der Quantentheorie
Ein Artikel von Markus Pössel
Der grundlegende Unterschied zwischen klassischer Physik und Quantentheorie besteht darin, dass es in der Quantenwelt weit weniger Gewissheiten gibt. Oft sind lediglich Aussagen dazu möglich, wie wahrscheinlich ein bestimmtes Messergebnis ist.
Ein Teilchen reist von A nach B
Ein Beispiel: Ein Teilchen läuft zur Zeit tA am Raumpunkt A los. Trifft es zu einem gegebenen späteren Zeitpunkt tB am Raumpunkt B ein?
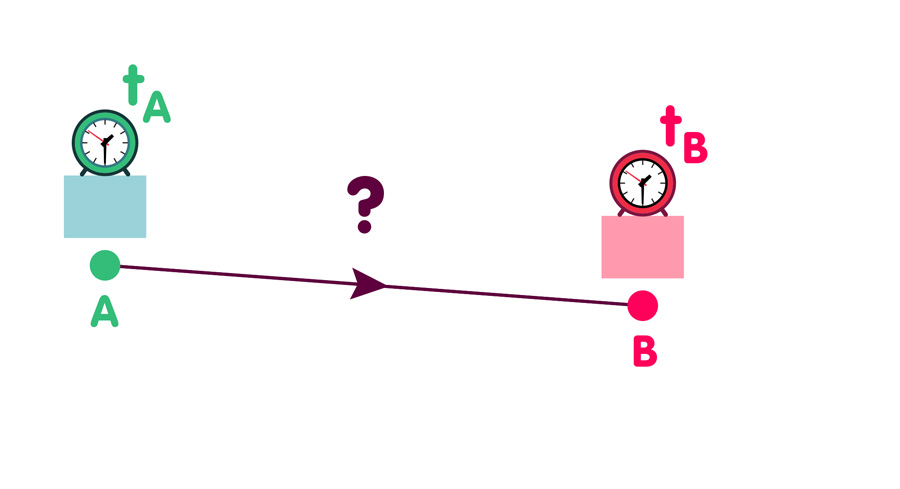
In der klassischen Physik fällt die Antwort eindeutig aus und ist, abhängig von der Anfangsgeschwindigkeit des Teilchens und von den Kräften, die auf das Teilchen wirken, Ja oder Nein. In der Quantentheorie dagegen lässt sich die Frage überhaupt nicht eindeutig beantworten. Man kann lediglich die Wahrscheinlichkeit dafür angeben, dass ein gegebenes Teilchen, das sich zur Zeit tA am Raumpunkt A befindet, zur Zeit tB am Raumpunkt B nachgewiesen werden kann.
Der von dem US-amerikanischen Physiker Richard Feynman erfundene Pfadintegral-Formalismus ist ein Werkzeug, das es erlaubt, solche Wahrscheinlichkeiten auszurechnen. Angewandt auf unser von A nach B reisendes Teilchen ist Feynmans Rezept für die Wahrscheinlichkeit das folgende.
Erstens: Betrachte alle Möglichkeiten, wie das Teilchen in der gegebenen Zeit von A nach B gelangen kann. Nicht nur langweilige Fälle wie einen geradlinigen, ereignislosen Direktflug von A nach B, sondern auch Flüge mit Umwegen und Loopings:
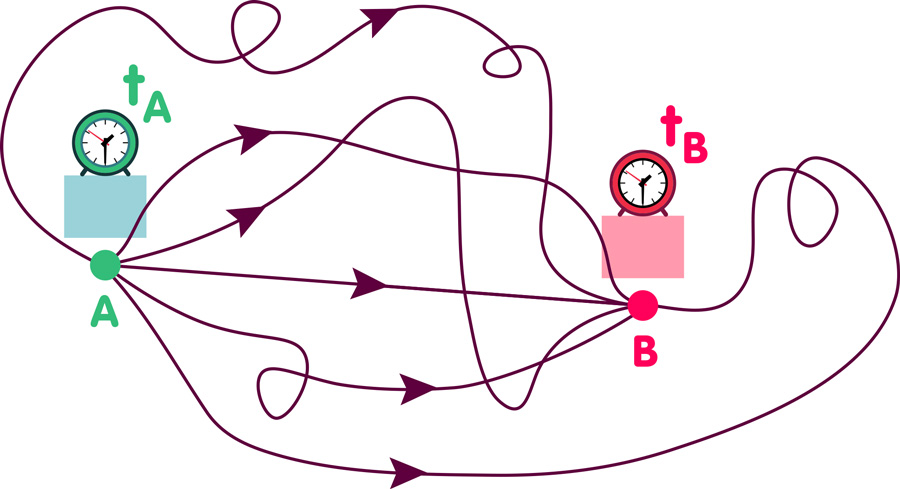
Dabei stapelt diese Grafik noch viel zu tief – sie zeigt lediglich sechs von unendlich vielen Reisemöglichkeiten und lässt beispielsweise die Fälle außen vor, in denen das Teilchen Abstecher zum Mond oder zur Andromeda-Galaxie macht, bevor es am Ort B eintrudelt. Auch geht verloren, wie das Teilchen seine Geschwindigkeit variieren kann – in einigen Fällen beispielsweise legt es den ersten Teil seiner Bahn atemberaubend schnell und die letzten Millimeter im Schneckentempo zurück, in anderen umgekehrt, in wieder anderen völlig anders – ein weiteres Feld mit unendlich vielen Variationsmöglichkeiten. Alle Reisemöglichkeiten müssen in diesem Schritt berücksichtigt werden, selbst die ausgefallendsten.
Im zweiten Schritt des Rezeptes wird jeder der Reisemöglichkeiten eine Zahl zugeordnet (nicht ganz die Art von Zahl, die wir aus der Schule kennen, sondern eine so genannte komplexe Zahl aber diese technische Feinheit soll uns nicht kümmern). Am Ende werden die Beiträge aller Reisemöglichkeiten addiert, einige Summanden heben sich dabei auf, andere verstärken sich. (Leser, denen dies bekannt vorkommt und die dabei an Wellen denken, seien versichert: ja, dies ist tatsächlich ein Beispiel für Interferenz.) Die Summe sagt uns die gewünschte Wahrscheinlichkeit dafür, das zur Zeit tA am Ort A gestartete Teilchen zur Zeit tB am Ort B nachzuweisen. Solch eine Summe über alle Reisemöglichkeiten heißt unter Physikern Pfadintegral.
Die etwas andere Zeit
Pfadintegrale konkret zu berechnen ist freilich mit einigen Schwierigkeiten verbunden. Ein wichtiges Beispiel bietet die Elementarteilchenphysik, deren grundlegende Modelle aus der Verbindung von Quantentheorie und Spezieller Relativitätstheorie hervorgehen. Dort ist das Pfadintegral ein wichtiges Werkzeug, um auszurechnen, wie Elementarteilchen miteinander wechselwirken. Die eigentliche Rechnung verwendet allerdings einen mathematischen Kunstgriff: Überall dort, wo in den Feynmanschen Formeln die Zeitkoordinate t auftaucht, fügt man einen Faktor i hinzu. Das i ist die so genannte imaginäre Einheit, ein algebraisches Symbol, das dadurch definiert ist, dass sein Quadrat den Wert minus Eins ergibt, i2=-1. Dann wird das Pfadintegral ausgerechnet, und am Ende wird die Einfügung all der Faktoren i wieder rückgängig gemacht.
Die Ersetzung mag künstlich und unmotiviert scheinen. In gewisser Weise hebt sie die Unterscheidung zwischen der Zeitkoordinate und den drei Raumkoordinaten auf. Entscheidend ist aber, dass das Feynmansche Rezept mit dieser Zusatzprozedur die richtigen Antworten für die Wahrscheinlichkeiten von Teilchenreaktionen liefert. Das lässt sich sogar exakt beweisen, wie zwei mathematische Physiker, der Schweizer Konrad Osterwalder und der Deutsche Robert Schrader zeigen konnten: Die Eigenschaften einer herkömmlichen Quantentheorie, die auf der Raumzeit der Speziellen Relativitätstheorie definiert ist, lassen sich exakt aus dem Feynman-Rezept für eine korrespondierende, „imaginärzeitige“ Raumzeit rekonstruieren.
Pfadintegrale und Quantengravitation
Auch in den Ansätzen für eine Theorie der Quantengravitation spielen Pfadintegrale eine Rolle. In der Stringtheorie beispielsweise lassen sich die Wahrscheinlichkeiten bestimmter Wechselwirkungen zwischen den Strings als Pfadintegral berechnen, bei dem zur Summe über alle Reisemöglichkeiten noch die Summe über alle Arten und Weisen hinzu kommt, auf die sich der String auf seiner Reise verbiegen und verformen kann. Andere Ansätze im Rahmen der so genannten Quantenkosmologie wenden Pfadintegrale (mit oder ohne das mysteriöse i) auf das Universum als Ganzes an um zu beschreiben, wie unser Kosmos seinen Anfang nahm. Die Wahrscheinlichkeit, dass sich das Universum hin zu einem bestimmten Zustand weiterentwickelt, ergibt sich dort aus der Summe aller Möglichkeiten, wie diese Entwicklung vor sich gehen kann – die Summe über alle Geschichtsverläufe, die vom Anfang des Universums bis zur Jetztzeit führen.
Weitere Informationen
Die Grundlagen von relativistischer Teilchenphysik und Quantengravitation werden in Einstein für Einsteiger erklärt, insbesondere im Abschnitt Relativität und Quanten.
Verwandte Vertiefungsthemen auf Einstein Online finden sich in der Kategorie Relativität und Quanten.
Kolophon
ist Astrophysiker am Max-Planck-Institut für Astronomie, Leiter des Hauses der Astronomie in Heidelberg und Initiator von Einstein Online.
Zitierung
Zu zitieren als:
Markus Pössel, “Auf allen möglichen Wegen zum Ziel” in: Einstein Online Band 02 (2006), 02-1115










