Ein Prüfstand für die Allgemeine Relativitätstheorie
Über ein Modell, in dessen Rahmen sich systematisch beschreiben lässt, wie gut (oder schlecht) Einsteins Theorie mit der Beobachtung übereinstimmt.
Ein Artikel von Gerhard Schäfer
In einem für kosmische Verhältnisse vergleichsweise schwachen Gravitationsfeld – etwa auf unserer Erde oder anderswo in unserem Sonnensystem – weichen die Vorhersagen der Newtonschen Gravitationstheorie und jene der Allgemeinen Relativitätstheorie nur sehr wenig voneinander ab. Die Physiker nutzen dies aus, um den Übergang von der einen Theorie zur anderen in nützlicher Weise zu systematisieren: Im Rahmen der so genannten post-Newtonschen Näherungen werden zur Newtonschen Theorie Schritt für Schritt Korrekturterme hinzugefügt, mit denen die Abweichungen der Einsteinschen von der Newtonschen Theorie näherungsweise berücksichtigt werden (nähere Informationen hierzu bietet das Vertiefungsthema Schritt für Schritt von Einstein zu Newton).
Der erste Schritt, in dem nur die wichtigsten Korrekturterme hinzutreten, führt zur so genannten ersten post-Newtonschen Näherung (1pN). Sie enthält bereits Beschreibungen etwa der Lichtablenkung im Schwerefeld und der relativistischen Periheldrehung. Anwendung findet diese Näherung zum Beispiel bei modernen Computerberechnungen der Planetenbahnen im Sonnensystem, aber auch in der Physik einander umkreisender Neutronensterne und der Gravitationslinsen-Astronomie. Die erste post-Newtonsche Näherung ist aber noch aus einem weiteren Grunde wichtig: Man kann sie so verallgemeinern, dass sich eine Art Prüfstand für die Allgemeine Relativitätstheorie ergibt!
Der Weg zur Test-Theorie
Die Allgemeine Relativitätstheorie lässt sich wie folgt charakterisieren: In dieser Theorie werden Newtonsche Gravitationstheorie und Spezielle Relativitätstheorie verallgemeinert und miteinander verbunden; eine wichtige Rolle spielt dabei das Einsteinsche Äquivalenzprinzip.
Umgekehrt genügen dieser Beschreibung allerdings eine ganze Reihe von Theorien, unter denen die Allgemeine Relativitätstheorie freilich die einfachste ist. Ein weiteres Beispiel für eine Theorie, die auf denselben Grundlagen aufbaut, ist die Jordan-Fierz-Brans-Dicke-Theorie, die oftmals nur Brans-Dicke-Theorie genannt wird. In dieser Theorie gibt es zusätzlich zur geometrischen Gravitation noch ein weiteres Gravitationsfeld, ein so genanntes Skalarfeld. Das Skalarfeld beeinflusst sowohl die Bewegung von Körpern als auch bestimmte Eigenschaften (die Polarisation) von Gravitationswellen.
Ebenso wie für die Allgemeine Relativitätstheorie kann man auch für die anderen Theorien eine Formulierung finden, die mit der Newtonschen Gravitationstheorie beginnt und ihr Schritt für Schritt Korrekturterme hinzufügt. Vergleicht man die erste post-Newtonsche Näherung der Allgemeine Relativitätstheorie mit derjenigen der Brans-Dicke-Theorie, so findet man bereits hier einen Unterschied: Die Korrekturterme haben zwar die gleiche Form, was beispielsweise ihre Abhängigkeit von den Massen der beteiligten Körper oder von der Gravitationskonstante angeht, doch die numerischen Vorfaktoren der einzelnen Terme weichen voneinander ab.
Das bedeutet aber auch, dass man – zumindest auf der Ebene der ersten post-Newtonschen Näherung – eine Art Rahmen schaffen kann, der alle genannten Theorien gleichermaßen enthält: Man führt ganz einfach eine Reihe neuer Parameter ein. Für einen der Korrekturausdrücke etwa gibt die Allgemeine Relativitätstheorie eine konkrete Form vor, die wir mit X abkürzen wollen. Dieser Ausdruck wird nun mit einem neuen Parameter multipliziert, den wir hier δ (Delta) nennen wollen, so dass dort nun statt des ursprünglichen Ausdrucks ein neuer Ausdruck δ·X steht. Ähnlich verfährt man mit den anderen Korrekturtermen – sie bekommen jeweils einen neuen Parameter als Vorfaktor. Für den Spezialfall, dass man all diese Parameter gleich eins setzt, erhält man die erste post-Newtonsche Näherung der Allgemeinen Relativitätstheorie. Für bestimmte andere Werte der Parameter erhält man die post-Newtonsche Näherung der Brans-Dicke-Theorie oder einer der anderen alternativen Theorien.
Man kann den Rahmen noch erweitern, indem man Korrekturterme einführt, die in der Allgemeinen Relativitätstheorie nicht auftreten und die für Phänomene stehen, die dieser Theorie gänzlich fremd sind. Ein Beispiel sind Korrekturen, die sich ergeben, wenn man annimmt, es gebe ein durch die physikalischen Gesetze bevorzugtes Bezugssystem, eine Art „absoluten Raum„. Andere Korrekturen kommen hinzu, wenn man annimmt, es gäbe bevorzugte Richtungen im Raum, und der Ausgang bestimmter physikalischer Experimente hinge davon ab, wie der Experimentalaufbau im Raum orientiert ist. Auch vor diese neuen Korrekturterme schreibt man freie Parameter. Setzt man diese Parameter zu Null, dann verschwinden die zusätzlichen Terme, und man bewegt sich wieder im Rahmen der Allgemeinen Relativitätstheorie.
Auf diese Weise gelangt man zu einem verallgemeinerten Formalismus, dem man den Namen parametrisierte post-Newtonsche Näherung gegeben hat, allgemein abgekürzt zu PPN. Die wesentlichen Grundlagen des PPN-Formalismus stammen von Arthur Eddington, Howard Robertson und Leonard Schiff; wichtige Beiträge aus neuerer Zeit stammen von Kenneth Nordtvedt und Clifford Will.
Der Nutzen der Verallgemeinerung besteht darin, dass die neuen Parameter es erlauben, die Allgemeine Relativitätstheorie quantitativ auf die Probe zu stellen.
Zum Beispiel können wir im Rahmen der verallgemeinerten Theorie ausrechnen, um welchen Winkel ein Lichtstrahl abgelenkt wird, der am Sonnenrand vorbeistreicht und einen Beobachter auf der Erde erreicht. Für den Winkel ergibt sich dann genau der gleiche Ausdruck wie in der Allgemeinen Relativitätstheorie, allerdings malgenommen mit einem Faktor (1+γ)/2. Dabei ist γ ein Parameter, der vor einem der post-Newtonschen Korrekturterme steht und in der Allgemeinen Relativitätstheorie den Wert 1 hat. Um wieviel das Licht tatsächlich abgelenkt wird, hängt damit von γ ab, wie in der nachfolgenden Animation zu sehen ist. Sie zeigt ein Objekt, das rund 6000 mal kompakter ist als die Sonne:

Aus Messungen des Ablenkungswinkels für Lichtablenkung am Sonnenrand lässt sich der Wert des Parameters γ direkt bestimmen, und man kann quantitativ angeben, wie nahe dieser Wert an der Vorhersage der Allgemeinen Relativitätstheorie liegt, also an dem Wert γ=1. Ebenso enthalten eine Reihe anderer Vorhersagen der Testtheorie, etwa zur anomalen Periheldrehung oder dem Einfluss der Raumzeit auf die Achsenrichtung von Kreiseln, explizit die neu eingeführten Parameter. Im Vergleich mit den Messungen lassen sich die Parameterwerte daher empirisch bestimmen, und es lässt sich quantitativ angeben, wie gut die aus den Beobachtungen gewonnenen Parameterwerte mit den von der Allgemeinen Relativitätstheorie geforderten Werten (eins oder null) übereinstimmen.
Die Parameter der Testtheorie
Im folgenden wollen wir die einzelnen Parameter der PPN-Theorie kurz Revue passieren lassen und ein wenig auf ihre physikalische Bedeutung eingehen.
Raumkrümmung und γ (Gamma)
Der Parameter γ ist bereits kurz angesprochen worden. Er beschreibt den Einfluss der Materie auf die Krümmung des Raumes. In der Allgemeinen Relativitätstheorie hat γ den Wert eins, in der Brans-Dicke-Theorie aber beispielsweise ist der Parameter immer kleiner als eins. Wenn die Materie die Raumkrümmung überhaupt nicht beeinflusst und der Raum daher auch in Anwesenheit von Materie die aus der Schule gewohnte euklidische Geometrie aufweist, dann ist γ=0. Dies ist beispielsweise in der Newtonschen Theorie der Fall.
Experimentell kann der Wert von γ durch Messungen der Lichtausbreitung bestimmt werden (der gravitationsbedingten Lichtablenkung wie in obiger Abbildung oder auch des Shapiro-Effekts). Den Beobachtungen nach weicht γ höchstens um einige Hunderttausendstel von dem durch die Allgemeine Relativitätstheorie vorhergesagten Wert ab. Eine Auswahl von Messdaten zeigt die folgende Abbildung:
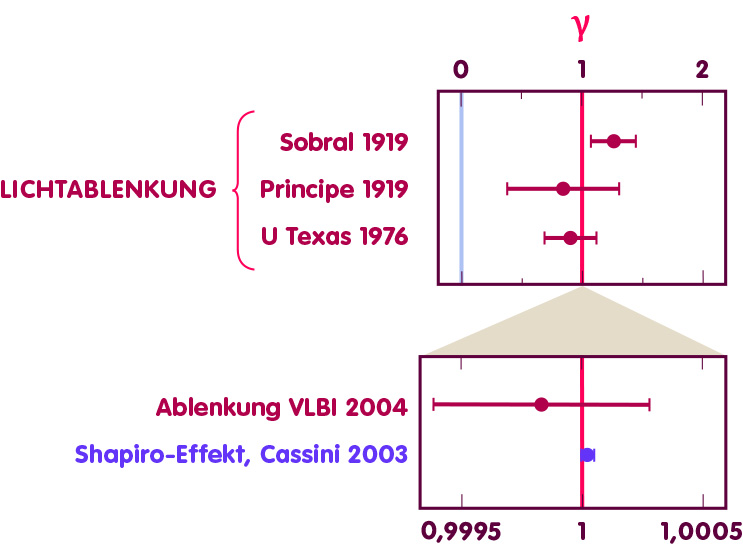
Das obere Diagramm deckt dabei für γ den Wertebereich von null (Newtonscher Wert, eingezeichnet als hellblaue Linie) bis zwei ab. Das untere Diagramm zeigt einen Detailausschnitt, in dem γ um nicht mehr als einem Zweitausendstel von eins abweicht. In dunkelroter Farbe sind die Ergebnisse von Messungen der Lichtablenkung eingezeichnet: die ersten zwei Messungen überhaupt, vorgenommen von der britischen Sonnenfinsternis-Expedition von 1919; eine von der Universität Texas vorgenommene Beobachtung aus dem Jahre 1973, und im unteren Diagramm die Messung von S. Shapiro und Kollegen aus dem Jahre 2004 an Radiowellen, welche das hochgenaue VLBI-Verfahren nutzt. Der in lila dargestellte Messpunkt entspricht einer Messung des Shapiro-Effekts mit Hilfe der Raumsonde Cassini im Jahre 2003 und liefert die bislang genaueste Bestimmung des Parameters γ.
Die Gravitation der Gravitation: β (Beta) und ξ (Xi)
Neben dem bereits genannten Parameter γ führt man den Parameter β ein, der in der Allgemeinen Relativitätstheorie ebenfalls den Wert eins besitzt, aber beispielsweise in Theorien mit einem zusätzlichen Skalar-Gravitationsfeld ungleich eins sein kann. Der Parameter gibt an, wie stark ein Gravitationsfeld seinerseits Gravitation hervorruft – ein Aspekt der so genannten Nichtlinearität der Gravitation (siehe hierzu das Vertiefungsthema Die Gravitation der Gravitation).
Diese Nichtlinearität macht sich etwa bemerkbar, wenn es darum geht, die Bahn des Erdmondes und des Merkurs zu berechnen; in den Korrekturtermen, die dafür eine Rolle spielen, tritt β zusammen mit γ auf. Außerdem sind die weniger wichtigen Parameter α1,2,3 und ζ2 mit von der Partie, auf die wir weiter unten noch kurz zurückkommen werden und die im Rahmen der ART Null sind. Die nachfolgende Abbildung zeigt die Merkurbahn; deren relativistische Periheldrehung – der Umstand, dass die Bahn nicht eine Ellipse, sondern eher rosettenförmig ist – hängt direkt mit β und γ zusammen. In der Abbildung ist die Merkurbahn in zweierlei Hinsicht überzeichnet, um den Effekt deutlich sichtbar werden zu lassen: Zum einen ist die Exzentrizität um den Faktor vier erhöht, also die Abweichung der Ellipse von einer Kreisbahn sehr viel stärker. Zum anderen ist die Periheldrehung selbst gegenüber dem wirklichen Merkur um den Faktor 200000 vergrößert. Die Animation zeigt, wie sich die Periheldrehung in Abhängigkeit von dem Wert von β ändert:
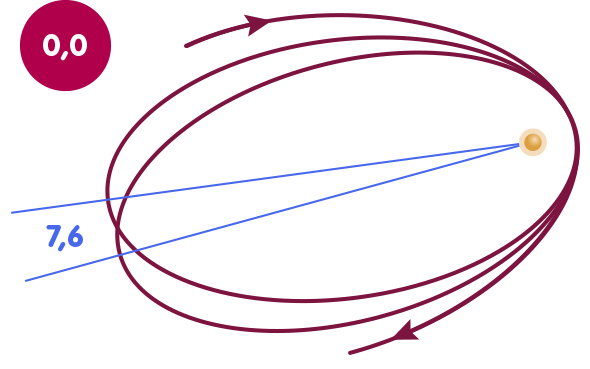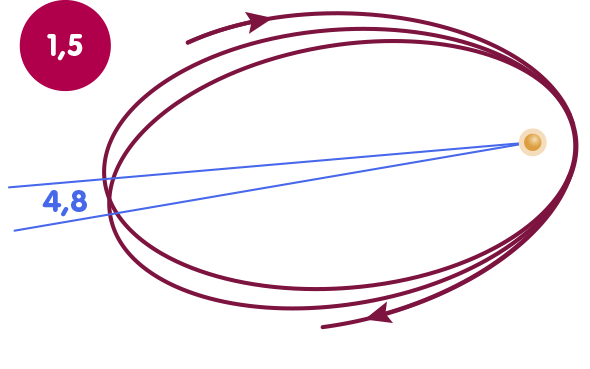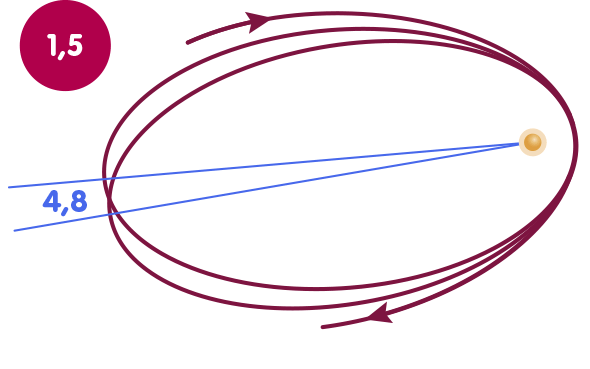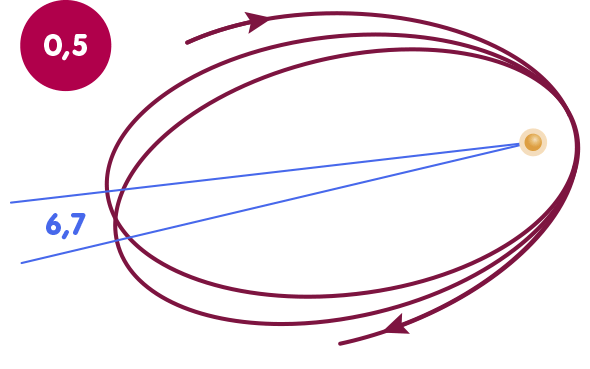
Um β zu bestimmen, zieht man dementsprechend Messungen der Bahnen der erwähnten Himmelskörper heran. Betrachten wir ein Diagramm, in dem jeder Punkt für ein bestimmtes Wertepaar für β und γ steht:
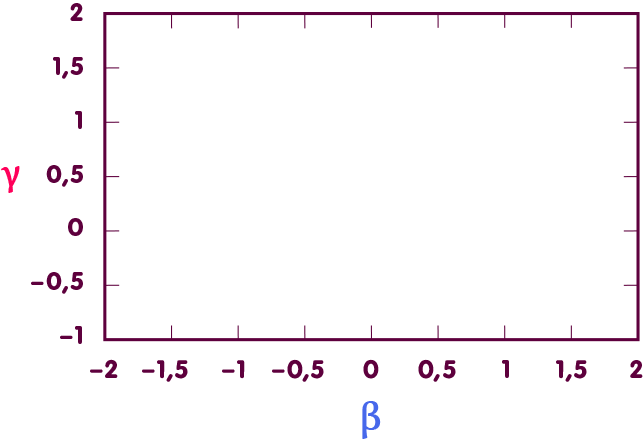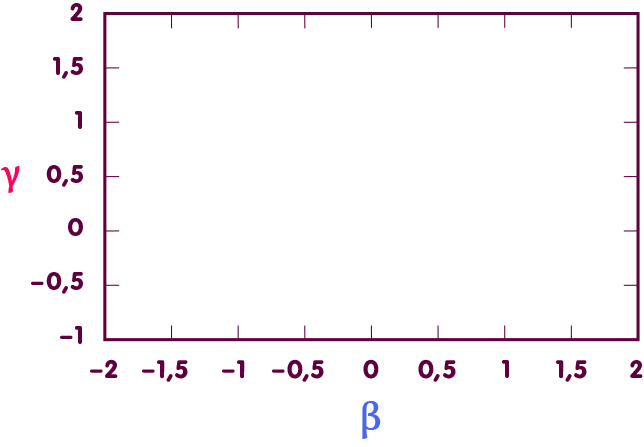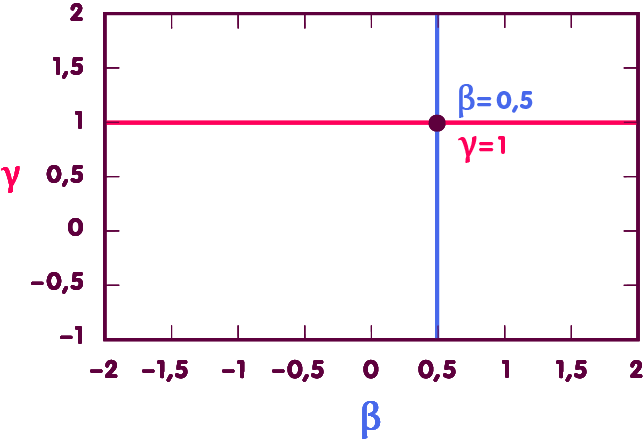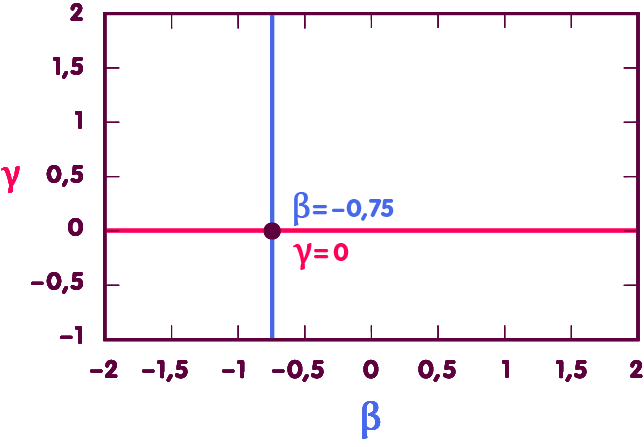
In solch einem Diagramm definieren die erwähnten Messungen eine Gerade zulässiger Wertepaare (in der nachfolgenden Abbildung die violette Linie). Dass γ, siehe oben, aus weiteren Messungen bekannt ist, definiert eine weitere Gerade zulässiger Werte, die waagerecht liegt (rote Linie). Am Schnittpunkt der Geraden liegt derjenige Punkt, der den tatsächlichen Werten von β und γ entspricht – und das exakt bei dem durch die ART vorhergesagten Wert β=1 (blaue Linie):
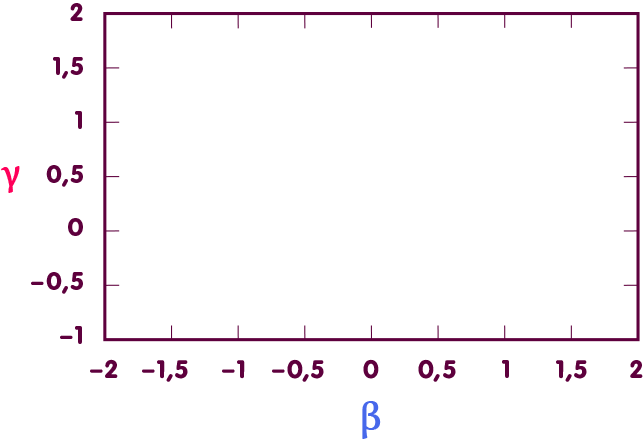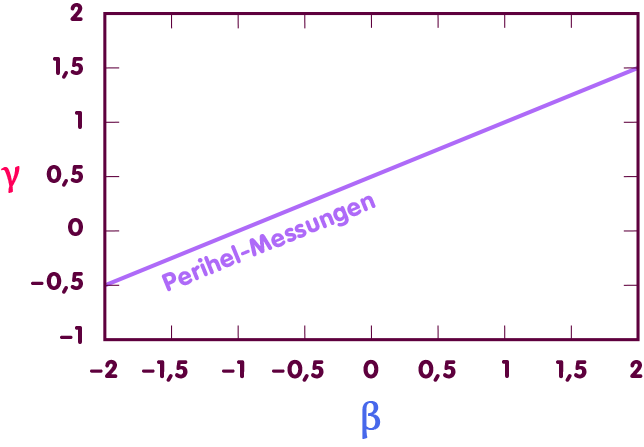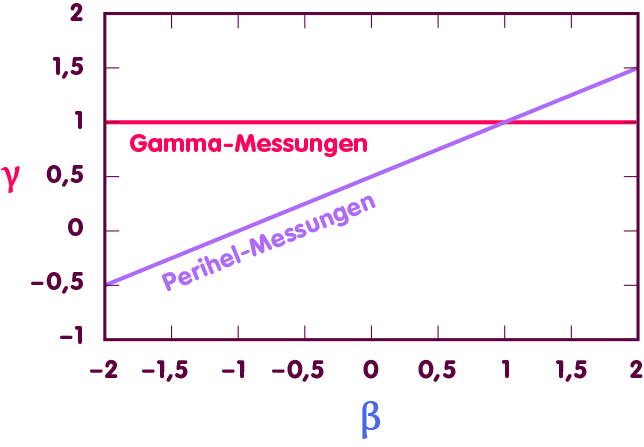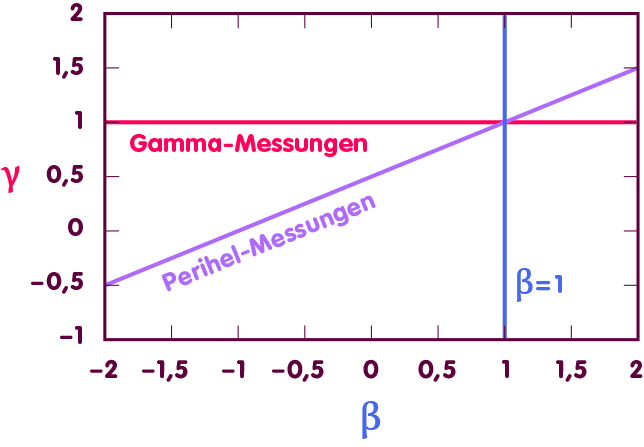
Dementsprechend weicht β höchstens um einige Zehntausendstel von dem durch die Allgemeine Relativitätstheorie vorgegebenen Wert ab.
Weitere Beobachtungen gelten der Bewegung von Weißen Zwergen um Neutronensterne (Pulsare) und beider wiederum in dem von allen Massen in unserer Galaxie erzeugten Gravitationsfeld. Dies sind Fälle sehr viel stärker gravitierender Körper, und auch diese Beobachtungen liefern Einschränkungen für die Parameterwerte β und γ, die im Einklang mit der Allgemeinen Relativitätstheorie stehen.
Exotischer ist der Parameter ξ (Xi), dessen Wert genau dann von null abweicht, wenn die Gravitation noch eine andere Form der Nichtlinearität aufweist als in der Allgemeinen Relativitätstheorie (in der Fachliteratur ist dies als Effekt bevorzugter Orte bekannt). In bisherigen Messungen findet sich kein Hinweis darauf, dass der Wert von ξ von dem durch die Allgemeine Relativitätstheorie vorhergesagten Wert Null verschieden wäre.
Bevorzugte Bezugssysteme und Erhaltungssätze: αs und ζs
Die Parameter α1, α2 und α3 beschreiben verschiedene Arten von Effekten, die auf bevorzugte Bezugssysteme hinweisen – auf eine Art absoluten Raum, in dem die Gesetze der Physik für Beobachter, die relativ zum absoluten Raum in Ruhe befindlich sind, besonders einfach werden. Sie sind in der Allgemeinen Relativitätstheorie sämtlich null.
Die Parameter ζ1, ζ2, ζ3 und ζ4 sind in der Allgemeinen Relativitätstheorie ebenfalls null. Sind entweder sie oder α3 ungleich Null, dann sind Energieerhaltung und Impulserhaltung verletzt. Energie beispielsweise könnte dann anscheinend aus dem Nichts erzeugt werden – was beispielsweise dann der Fall sein könnte, wenn es uns unbekannte (und daher in der Theorie nicht berücksichtigte), Wechselwirkungen mit langer Reichweite gibt, über die Energie aus anderen Teilen des Universums in unser Sonnensystem transportiert würde.
Sind alle α- und ζ-Parameter gleich null, dann gelten auch noch der Drehimpuls- und Schwerpunktssatz: Drehimpuls, eine mit der Rotation von Körpern verbundene Größe, kann dann weder aus dem Nichts erzeugt noch vernichtet werden, und die Bewegung des Schwerpunkts eines Systems verläuft so, als würden alle äußeren Einflüsse direkt an diesem Punkt angreifen.
Es gibt in Beobachtungen und Experimenten keinen Hinweis darauf, dass die Werte von α1, α2, α3, ζ1, ζ2, ζ3 und ζ4 von null abweichen.
Ein Sonderfall: Zeitdehnung und α (Alpha)
Bisweilen wird bei Tests der Allgemeinen Relativitätstheorie auch ein Parameter α verwendet, der nicht zu den PPN-Parametern gehört, aber wie diese verwendet werden kann, um bestimmte Vorhersagen der Allgemeinen Relativitätstheorie zu prüfen. Er hängt direkt mit dem Einfluss der Gravitation auf die Zeit zusammen.
Auch α hat in der Allgemeinen Relativitätstheorie den Wert eins (ebenso wie die PPN-Parameter β und γ). Was die Bewegung von Körpern im Gravitationsfeld angeht, gehört der betreffende Term allerdings nicht zu den Korrekturen, die erst durch die Allgemeine Relativitätstheorie hinzutreten, sondern er ist bereits Teil der Newtonschen Gleichungen. Dementsprechend ist bereits aus den herkömmlichen Beobachtungen der Planetenbahnen bestens bekannt, dass es sich tatsächlich um den von Newton und Einstein vorhergesagten Ausdruck handelt.
Der Grund, α trotzdem als freien Parameter einzuführen, ist, dass der betreffende Term in der Allgemeinen Relativitätstheorie eine Doppelrolle spielt und außer für die Bewegung von Körpern zusätzlich für Effekte zuständig ist, die der Newtonschen Theorie fremd sind. Dabei handelt es sich um die (gut messbare) Frequenzänderung von Licht im Gravitationsfeld bzw. um den damit unmittelbar zusammenhängenden Uhrengangunterschied (gravitative Zeitdehnung). Die Messung dieser Effekte bietet einen hochgenauen Zugang zur Messung von α – und dieser Parameter bietet seinerseits die Möglichkeit, quantitativ auszudrücken, wie gut die Vorhersagen der Allgemeinen Relativitätstheorie zur gravitativen Frequenzverschiebung und Zeitdehnung mit den Beobachtungen übereinstimmen. Die nachfolgende Abbildung zeigt einige ausgewählte Messwerte zur Bestimmung von α:
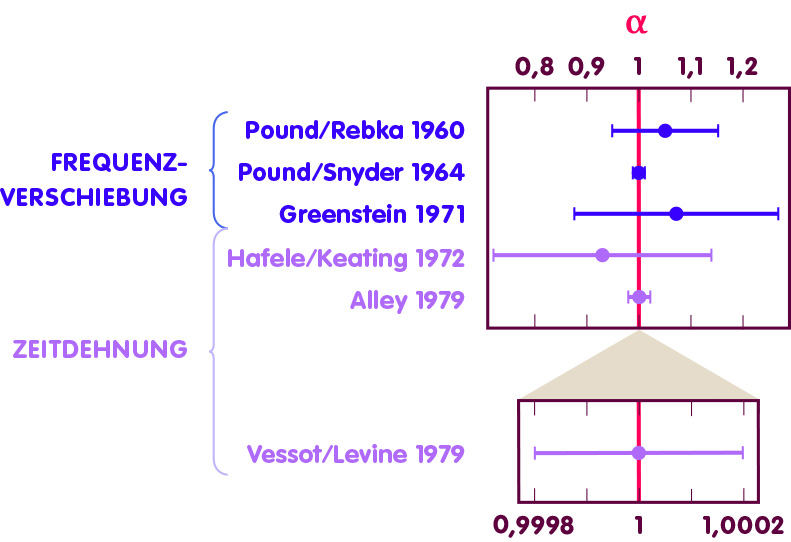
Gezeigt sind dabei Messungen der Frequenzverschiebung (blaue Datenpunkte) und Messungen, bei denen die Zeitdilatation mit Hilfe von Atomuhren gemessen wird (hellviolette Datenpunkte). Die Experimente von Pound und Mitarbeitern haben die Frequenzverschiebung im Labor mit Hilfe von Gammastrahlen gemessen (und zwar mit Hilfe so genannter Mößbauer-Spektroskopie an Atomkernen des Isotops Eisen-57). Greenstein und Kollegen werteten astronomische Beobachtungen des Weißen Zwergsterns Sirius B aus. Hafele/Keating und Alley ließen von der Erde aus Atomuhren mit Flugzeugen aufsteigen. Die genauesten Werte lieferte das 1976 durchgeführte Experiment von Vessot und Levine, genannt Gravity Probe-A, bei dem eine hochgenaue Maser-Uhr mit einer Rakete in die Höhe reiste. Die Genauigkeit ist so hoch, dass der Fehlerbalken nur in dem Detailausschnitt des unteren Diagramms zu sehen ist. Das Experiment ergab, dass der Wert von α mit einer Genauigkeit von fast einem Zehntausendstel mit der Vorhersage der Allgemeinen Relativitätstheorie übereinstimmt.
Hat man α eingeführt, dann hat auch der oben gezeigte Koeffizient des Ablenkungswinkels von Licht im Gravitationsfeld der Sonne eine etwas andere Form – anstelle des dort erwähnten (1+γ)/2 steht dann (α+γ)/2.
So nützlich α bei Messungen von Frequenzverschiebung und Zeitdilatation auch ist – bei modernen Messungen zur Genauigkeit der Allgemeinen Relativitätstheorie werden die Ergebnisse dieser Experimente vorausgesetzt, und man rechnet von vornherein mit α gleich eins.
Ausblick
Insgesamt gibt es im parametrisierten post-Newtonschen Formalismus zehn Parameter (elf, wenn man den Außenseiter α hinzunimmt). Ganze acht dieser Parameter sind in der Allgemeinen Relativitätstheorie null – ein Zeichen für die geradezu minimalistische Natur der Theorie als einfachste Verallgemeinerung der Newtonschen Gravitationstheorie, die mit den Beobachtungen im Einklang steht.
Insbesondere diejenigen Parameter, die in der Allgemeinen Relativitätstheorie nicht verschwinden – γ, β und der Außenseiter α – spielen eine entscheidende Rolle, wenn es darum geht, Beobachtungen und Experimente aus dem Wirkungsbereich der Allgemeinen Relativitätstheorie auszuwerten. Die Ergebnisse sind dann oft direkt durch diese Parameter ausgedrückt – geht es beispielsweise um Beobachtungen der Lichtablenkung, so wird man als Schluss oft eine Aussage wie jene lesen können, die Beobachtungen führten auf γ=0.99983± 0.00045, also auf einen bestimmten Wert für γ, der wie üblich mit einer bestimmten Messungenauigkeit behaftet ist.
Wie eingangs kurz erwähnt, berücksichtigt der PPN-Formalismus nur die einfachsten Korrekturterme zur Newtonschen Gravitationstheorie – die so genannte erste post-Newtonsche Näherung (1pN). Der Vollständigkeit halber sei angemerkt, dass es bestimmte Verallgemeinerungen auf die nächste Ebene der post-Newtonschen Näherung gibt (2pN), auf der dann noch deutlich mehr Terme berücksichtigt werden. Allerdings erfasst diese Verallgemeinerung nicht alle denkbaren Modelle, sondern beschränkt sich hauptsächlich auf den Spezialfall von Körpern, die sich zwar im gegenseitigen Gravitationsfeld bewegen, sich dabei aber nicht besonders schnell um die eigene Achse drehen.
Weitere Informationen
Hintergrundwissen zu diesem Vertiefungsthema bietet der Abschnitt Allgemeine Relativitätstheorie von Einstein für Einsteiger.
Verwandte Vertiefungsthemen auf Einstein Online finden sich in der Kategorie Allgemeine Relativitätstheorie.
Die in diesem Text verwandten Konventionen zur Benennung der PPN-Parameter entsprechen denen von Clifford Will. Fachlich anspruchsvollere Informationen zum Thema bietet Wills Artikel The Confrontation between General Relativity and Experiment (Living Reviews in Relativity).
Kolophon
ist Professor für Theoretische Physik und Relativistische Astrophysik an der Friedrich-Schiller-Universität in Jena.
Zitierung
Zu zitieren als:
Gerhard Schäfer, “Ein Prüfstand für die Allgemeine Relativitätstheorie” in: Einstein Online Band 04 (2010), 03-1107