The sum over all possibilities: The path integral formulation of quantum theory

About the path integral approach to quantum theory

An article by Markus Pössel

A fundamental difference between classical physics and quantum theory is the fact that, in the quantum world, certain predictions can only be made in terms of probabilities

A travelling particle

As an example, take the question whether or not a particle that starts at the time t_A at the location A will reach location B at the later time t_B.

Particle travelling from A to B

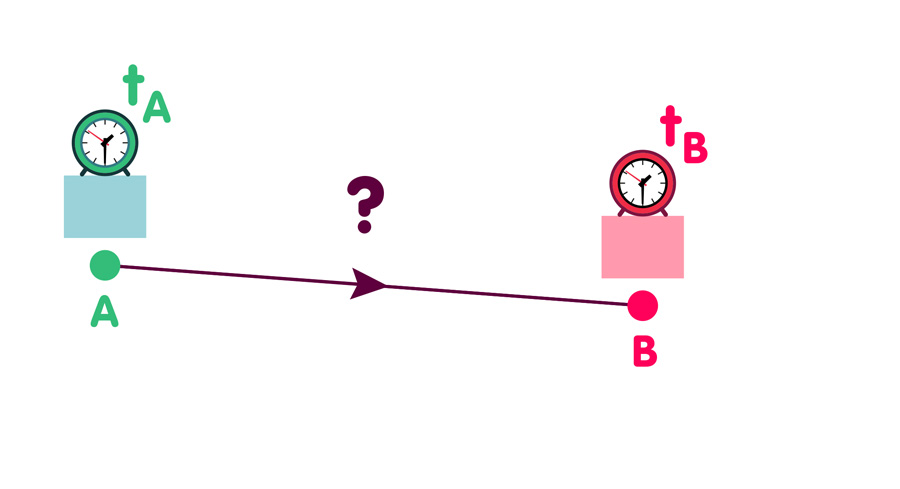
Classical physics can give a definite answer. Depending on the particle’s initial velocity and the forces acting on it, the answer is either yes or no. In quantum theory, it is merely possible to give the probability that the particle in question can be detected at location B at time t_B.

The path integral formalism, which was invented by the US physicist Richard Feynman, is a tool for calculating such quantum mechanical probabilities. Feynman’s recipe, applied to a particle travelling from A to B, is the following.

Step 1: Consider all possibilities for the particle travelling from A to B. Not only the boring straight-line approach, but also the possibility of the particle turning loopings and making diverse detours:

Particle travelling from A to B along multiple paths

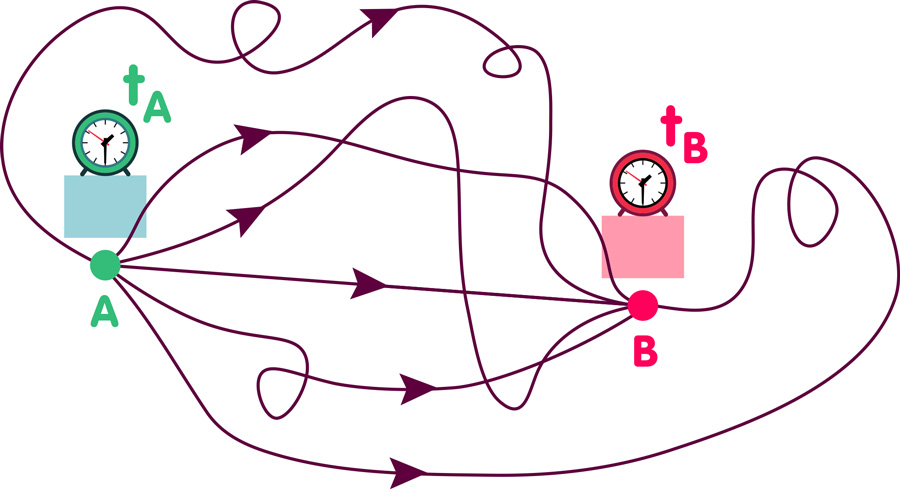
The illustration hardly does the particle justice. It shows a mere six from an infinity of possibilities. It neglects to show the cases in which the particle visits New York, Ulan Bator, or even the moon or the Andromeda Galaxy before arriving at its destination. Last but not least, it does not contain information about velocities. The first part of the particle’s trajectory may be travelled at break-neck speed and the final millimetres at a snail’s pace – or the other way around, or completely different; another infinity of possibilities. In short, for the first step, take into account all ways of travelling from A to B, however outlandish they may seem.

The second step is to associate a number with each of these possibilities (not quite the kind of number we’re used to from school, but we will not bother with the difference here). Finally, the numbers associated with all possibilities are added up – some parts of the sum canceling each other, others adding up. (Readers whom this makes think of waves are on the right track – it is an example of an interference phenomenon.) The resulting sum tells us the probability of detecting the particle that started out at A at the location B at the specified time. Physicists call such a sum over all possibilities a path integral or sum over histories.

A different kind of time

However, actually calculating such path integrals can be rather tricky. As an example, take particle physics, whose theories are a combination of quantum theory and special relativity. There, path integrals are an important tool to calculate the probability of particles interacting with each other in a given way. But there’s a catch, and in order to actually perform such calculations, one needs to resort to a mathematical trick: Everywhere that Feynman’s formula contains the time coordinate t, this t gets an extra factor i. Here, i is the so-called “imaginary unit”, an algebraic symbol that, by definition, squares to minus one,i²=-1. (The resulting pair i·t is sometimes called “imaginary time”.) After the path integral calculation is done, one reverses this substitution.

The replacement might seem artificial and implausible. In a way, it corresponds to transforming the time coordinate into just another space coordinate. Fact is, it makes the Feynman recipe give the right answers. There’s even an exact proof, found by two mathematical physicists, Konrad Osterwalder from Switzerland and the German Robert Schrader: They proved a theorem showing that the properties of a quantum theory formulated in the spacetime of special relativity can indeed be reconstructed exactly by using the Feynman recipe on an imaginary-time version of that same spacetime.

Path integrals and quantum gravity

Path integrals also play a role in some of the candidate theories for a theory of quantum gravity. In string theory, for instance, the probability of given string interactions can be calculated as a path integral – in addition to all possibilities a string can travel through space, the sum is over all possibilities the string can deform and wiggle on the way.

Also, in the context of what is called quantum cosmology, some proposals for how the universe might have begun (including its “initial state”) are formulated using path integrals, with or without the mysterious factor i. In this framework, the probability of the universe evolving into a certain state results from the sum over all possibilities for how this evolution might take place – literally a sum over all possible histories of the universe from its initial state to the present. However, the mathematical basis for defining path integrals where the curved spacetime of general relativity comes into play leads to some problems that, as of yet, have not been resolved completely.

Further Information

Some basics of relativistic particle physics and quantum gravity can be found in Elementary Einstein in the section Relativity and the quantum.

Quantum cosmology based on path integrals is described in the spotlight topic Searching for the quantum beginning of the universe. Related Spotlights on relativity can be found in the section Relativity and the quantum.

Colophon

Markus Pössel

is the managing scientist at Haus der Astronomie, the Center for Astronomy Education and Outreach in Heidelberg, and senior outreach scientist at the Max Planck Institute for Astronomy. He initiated Einstein Online.

Citation

Cite this article as:
Markus Pössel, “The sum over all possibilities: The path integral formulation of quantum theory” in: Einstein Online Band 02 (2006), 02-1020

Definitioner

waves (wave)

In a general sense: any travelling pattern, whether or not it involves matter being transported as well. Simple examples are water-waves - wave crests and troughs travelling over a water surface, and a Mexican wave in a football stadium, with fans alternately standing up and sitting down - the pattern moves throught the stadium, not the fans themselves.

An especially simple form for a wave is a sinus wave, a regular pattern of wave crests and troughs.

velocity

In physics, velocity is a combination of two aspects: First of all, how fast an object is, in other words: how long a distance it moves in a given time (its "speed"). Secondly, the direction in which an object moves. Physicists combine these two informations into a single mathematical object, called a "vector", and this is what is called the velocity. For instance, when a car goes around a curve with 100 miles per hour, its speed is constant, but as it changes its direction of movement, its velocity changes correspondingly.

time

It is a fact of life that not all events in our universe happen concurrently - instead, there is a certain order. Defining a time coordinate or defining time, the way physicists do it, is to define a prescription to associate with each event a number so as to reflect that order - if event B happens after event A, then the number associated with B should be larger than that associated with A. The first step of this definition is to construct a clock: Choose a simple process that repeats regularly. (What is "regular"? Luckily, in our universe, all elementary processes such as a swinging pendulum, the oscillations of atoms or of electronic circuits lead to the same concept of regularity.) As a second step, install a counter: A mechanism that, with every repetition of the chosen process, raises the count by one. With this definition, one can at least assign a time (the numerical value of the counter) to events happening at location of the clock. For events at different locations, an additional definition is necessary: One needs to define simultaneity. After all, the statement that some far-away event A happens at 12 o'clock is the same as saying that event A and "our clock counter shows 12:00:00" are simultaneous. The how and why of defining simultaneity - a centre-piece of Einstein's special theory of relativity - are described in the spotlight topic Defining "now". With all these preparations, physicists can, in principle, assign a time coordinate value ("a time") to any possible events, and describes how fast or how slow processes happen, compared to that time coordinate.

string (string theory)

Candidate for a theory of quantum gravity; a quantum theory, where the fundamental building blocks are tiny, one-dimensional, oscillating entities, called strings. A brief description can be found on the page String theory in the chapter Relativity and the quantum of Elementary Einstein.

speed

An object's average speed is the distance it moves during a given period of time, divided by the length of the time interval. If you make the time interval infinitely small, the result is the object's speed at one particular moment in time. The notion of speed can be applied to waves in different ways; for instance, for a simple wave, the phase speed is the speed at which any given wave crest or wave propagates through space. See also the more general entry velocity.

special relativity

Albert Einstein's theory of the fundamentals of space, time, and movement (but not gravity). For a brief introduction, check out the chapter Special relativity of Elementary Einstein. Selected aspects of special relativity are described in the category Special relativity of our Spotlights on relativity.

space

In a strict sense: Space as we know it from everyday life: the totality of all locations in which objects can sit, with three dimensions. In a more general sense used by mathematicians, all kinds of sets of points are spaces - a line for instance, which has but a single dimension, or a two-dimensional surface, but also higher-dimensional spaces. Also, in such more general spaces, geometry can be different from the standard Euclidean geometry taught in high schools - such spaces can be curved.

spacetime

Already in special relativity, observers in motion relative to each other will not, in general, agree as to whether two events happen simultaneously, or as to how great is the distance between two objects. They do, however, agree as to what events there are, although not to when and where they happen. This observer-independent totality of all events is called spacetime. How spacetime is split into space and time can differ from observer to observer. Every-day space has three dimensions. Adding time adds another dimension - spacetime has four dimensions, all in all. We are used to the idea of a point in space - an object that has only one location and is completely defined once its space coordinates are given. In spacetime, a spacetime point is an object defined completely once its space coordinates and its time coordinate are given - which makes a spacetime point nothing but an elementary event. The idea of spacetime is, in addition to its role in special relativity, a building block of general relativity. Analogous to how a plane is flat, but the surface of a sphere is curved, in general relativity, curved or distorted versions of the simple, flat spacetime of special relativity play a role. Spacetime curvature, in general relativity, is intimately connected with gravity. For an introduction to the basics of both theories of relativity, check out the chapters Special relativity and General relativity in Elementary Einstein. Sometimes, it can be helpful to view spacetime in analogy to ordinary space - such analogies are explored in the spotlight topics Time dilation on the road (for time dilation) and Twins on the road (for the twin effect).

second

In the International System of units: the basic unit of time. Defined as a certain multiple of the oscillation period of electromagnetic radiation set free in a certain transition within the electron shell of atoms of the type Cesium-133.

relativistic

Models, effects or phenomena in which special relativity or general relativity play a crucial role are called relativistic. Examples are relativistic quantum field theories as theories based on special relativity, or the relativistic perihelion shift as a consequence of general relativity. In addition, conditions under which the difference between relativistic physics and ordinary, classical physics are especially pronounced, are also called relativistic. For instance, when material objects reach speeds close to speed of light, one talks of relativistic speeds, while speeds that are so small compared to light as to make relativistic effects undetectably small are non-relativistic.

quantum theory

The framework for formulating the physical laws that govern the world at microscopic length-scales - the physics of the micro-world, for instance of atoms, atomic nuclei or elementary particles, but also the physics of ultra-precise measurements such as those made by gravitational wave detectors.

The laws of quantum theory are fundamentally different from our everyday experience and from those of classical physics.

The first unusual feature is that, in many cases, quantum theory merely allows statements about probabilities. For instance, in classical physics, one can assign to every particle, at every point in time, a location and a velocity. Whosoever can measure those quantities precisely can, in principle, predict where the particle in question can be found at every point in the future. In quantum theory, all one can assign to a system of particles is an abstract quantum state from which can be derived no precise predictions, but merely the probabilities for detecting a specific particle at a given time in a given place. Whether or not one will really find the particle at that location is governed by chance.

The second unusual feature is a fundamental restriction placed on the exactness of certain measurements (Heisenberg uncertainty relation). For instance, the more precise one measures a particle's location, the less definite any statements one can make about its velocity.

The third feature is how quantum theory came by its name: A number of physical quantities in nature come in little packets, in quanta. For instance, according to quantum theory, electromagnetic radiation is made of tiny quanta of energy called photons.

Examples for quantum theories are quantum mechanics and relativistic quantum field theories such as Quantum electrodynamics or other parts of the standard model of particle physics.

quantum gravity

Theory based both on the effects, concepts and laws of quantum theory and on those of general relativity. To date, no complete such theory exists; the best-known candidate theories are string theory and loop quantum gravity. Some information on the question of quantum gravity can be found in the chapter Relativity and the quantum of Elementary Einstein, starting with the page Border regions of gravity. Selected aspects of quantum gravity are described in the category Relativity and the quantum of our Spotlights on relativity.

relativistic (perihelion advance, relativistic)

For planetary orbits, there is a small difference between the predictions of Newtonian gravity and general relativity. For instance, in Newton's theory, the orbital curve of a lonely planet orbiting a star is an ellipse. In general relativity, it is a kind of rose or rhodonea curve. Such a curve is similar to an ellipse curve, which shifts a bit with each additional orbit. The shift can be defined by looking at the point which is closest to the sun (perihelion) on each orbit. The additional relativistic shift is, hence, called relativistic perihelion shift or relativistic perihelion advance. A picture can be seen on the page A planet goes astray in the chapter General relativity of Elementary Einstein.

path integrals

Synonym: Sum over histories. A technique for performing calculations in quantum theory. Roughly speaking, the probability for a certain outcome (for instance, a particle reaching location A at time t) is calculated by performing a sum over all possible ways in which this particular outcome can come about. A description of the path integral formulation of quantum theory can be found in the spotlight text The sum over all possibilities.

particle physics

The branch of physics that deals with particles that are, to the best of today's knowledge, not made up of more fundamental sub-units, for instance with electrons, quarks or neutrinos. Also included is the study of some species of particles that do have more elementary constitutents, such as protons or neutrons, but not of larger systems such as atomic nuclei (that would be nuclear physics) or, even worse, whole atoms. Questions such as, whether the particles nowadays thought to be elementary really are elementary, or are, for instance, different manifestations of one and the same species of string, fall within the scope of particle physics. The theoretical tools of particle physics are the so-called quantum field theories which allow the description of elementary particles on the basis of both quantum theory and special relativity, while the main experimental tools are particle accelerators in which particles are accelerated and then brought to collision.

line

Geometric object with a single dimension. A line can either be an independent one-dimensional space (in the abstract mathematical space where a space does not need to have three dimensions), or it can be embedded into a more general space, like a line drawn onto a piece of paper (i.e. a surface).

imaginary time

Certain quantum calculations (notably the calculation of path integrals as a way to find quantum mechanical probabilities) involve an algebraic manipulation of the following kind: Wherever the time coordinate t occurs, it is replaced by i·t, where i is the "imaginary unit", a number defined to have the remarkable property i²=i·i=-1. At the end of the calculation, the substitution is reversed. The combination T=i·t is called imaginary time. Most such calculations occur in particle physics, in the framework of special relativity, where there are rigorous mathematical proofs showing how the use of imaginary time leads to correct results. Imaginary time has also been employed in some candidate theories for a theory of quantum gravity, notably in certain types of quantum cosmology. This, however, involves the flexible time of general relativity, and both the details of the imaginary time recipe and the more general question whether or not imaginary time can usefully be employed in this context in the first place are still unresolved, and the object of current research. Some more information about path integrals and the role of imaginary time can be found in the spotlight text The sum over all possibilities, while imaginary time in quantum cosmology is briefly discussed in Searching for the quantum beginning of the universe.

gravity

See gravitation

gravity (gravitation)

In classical physics: An action-at-a-distance force by which all bodies that possess mass attract each other (see Newtonian theory of gravity), synonym: gravitational force. In Einstein's general theory of relativity: The fact that matter that possesses mass, energy, pressure or similar properties distorts spacetime, and that this distortion in turn influences whatever matter might be present. An introduction to the basic ideas of general relativity is provided by the section General relativity of Elementary Einstein. More information about the nature of gravity in general relativity can be found in the spotlight text Gravity: From weightlessness to curvature.

cosmology

That branch of physics and astronomy dealing with the structure and development of the universe as a whole. At the core of modern cosmology are the big bang models based on Einstein's general theory of relativity. Their basic features are reviewed in the chapter Cosmology of Elementary Einstein. In order to describe the very early universe, it will be necessary to take the effects of quantum gravity into account - this gives rise to models of quantum cosmology.