Spezielle Relativitätstheorie / Einsteiger-Tour Teil 4: Die konstante Lichtgeschwindigkeit
Im letzten Abschnitt hat sich vieles, was wir im Alltag als absolut betrachten, als beobachterabhängig-relativ herausgestellt. In diesem Abschnitt geht es um eine Größe, die, ebenso überraschend, unabhängig vom Beobachter und in diesem Sinne absolut ist: die Lichtgeschwindigkeit.
Unserem Alltagsverständnis nach würden wir erwarten, dass zwei relativ zueinander bewegte Beobachter – selbst, wenn sie ihre Maßeinheiten für Länge, Zeit und Geschwindigkeit gleich definieren – für ein und dasselbe Lichtsignal unterschiedliche Geschwindigkeiten messen. Das ergibt sich daraus, wie wir es im Alltag gewohnt sind, Relativgeschwindigkeiten zu ermitteln.
Angenommen, ich stehe am Autobahnrand und sehe zwei Autos in gleicher Richtung vorbeifahren. Für jedes der beiden ergibt meine Geschwindigkeitsmessung eine Geschwindigkeit von 100 Stundenkilometern:
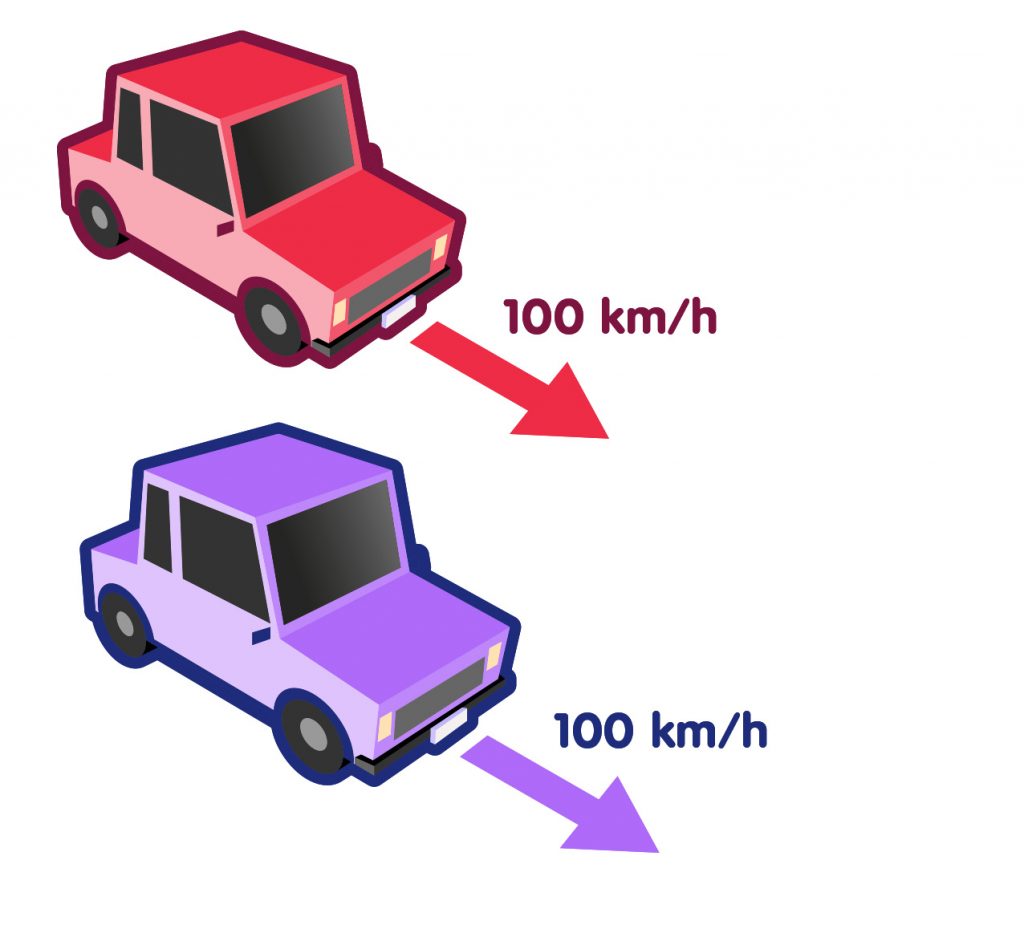
Zwei Autos mit je 100 km/h Geschwindigkeit
Daraus schließe ich, dass sich aus Sicht jedes der Autofahrer das jeweils andere Auto relativ zum eigenen Wagen überhaupt nicht bewegt. Hätte ich stattdessen für eines der Autos eine Geschwindigkeit von 120 Stundenkilometern gemessen,
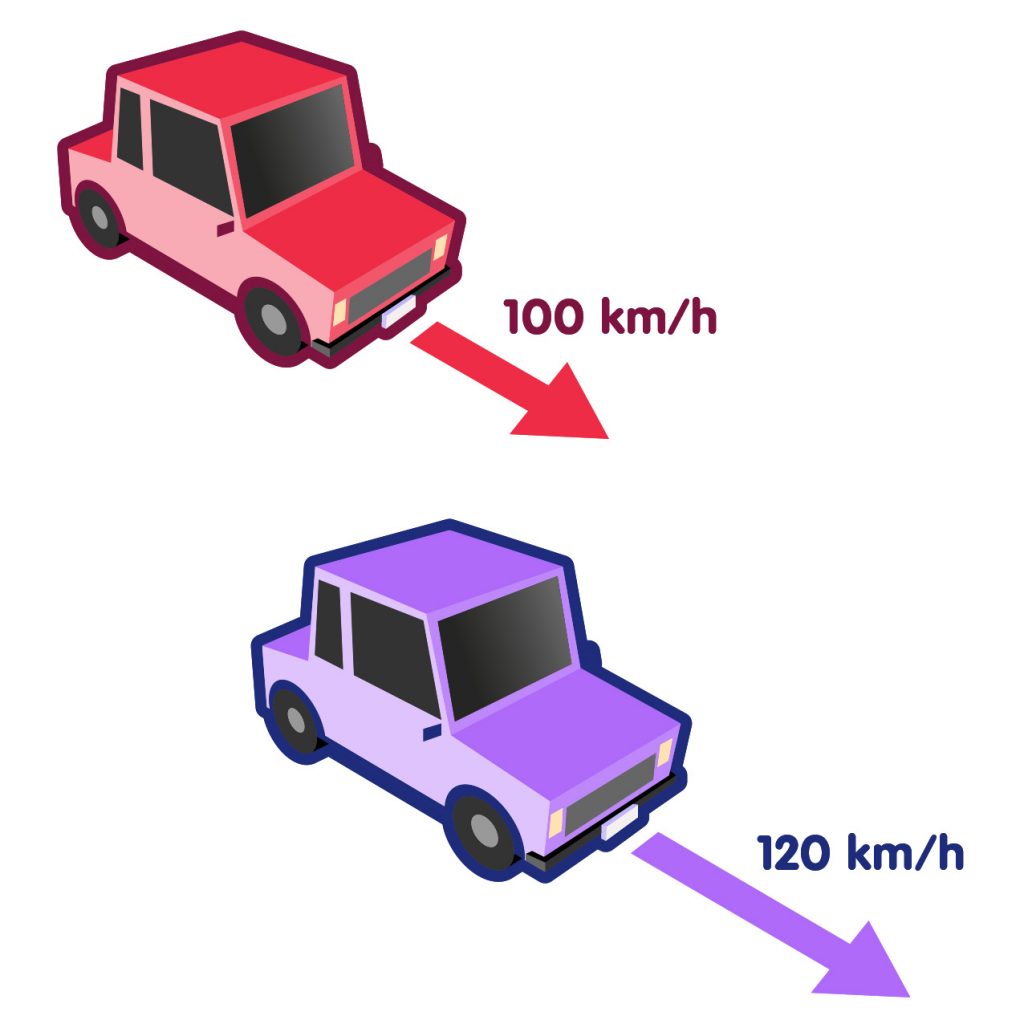
Ein Auto mit 100 km/h, eines mit 120 km/h Geschwindigkeit
so würde ich schließen, der Fahrer des langsameren Wagens sehe das schnellere Auto relativ zu seinem eigenen mit 20 Stundenkilometern davonziehen. In beiden Fällen ziehe ich die von mir gemessenen Geschwindigkeiten voneinander ab, um die Relativgeschwindigkeit zu erhalten: 100 minus 100 Stundenkilometer sind null Stundenkilometer Relativgeschwindigkeit im ersten Fall, 120 minus 100 Stundenkilometer sind 20 Stundenkilometer Relativgeschwindigkeit im zweiten Fall.
Für Licht könnte man vor diesem Hintergrund ähnliches erwarten: Angenommen, ich messe für ein Lichtsignal die übliche Geschwindigkeit von c = 299 792,458 Kilometer pro Sekunde und sehe ferner, wie ein Raumschiff diesem Lichtsignal mit c/2, also der Hälfte dieser Geschwindigkeit, hinterherfliegt. Dem Alltagsdenken folgend könnte man meinen, von diesem Raumschiff aus gesehen müsste das vorauseilende Licht eine Geschwindigkeit von nur c – c/2 = c/2 haben, also die Hälfte der Lichtgeschwindigkeit, die ich messe.
Laut Spezieller Relativitätstheorie ist das allerdings nicht der Fall. Meine Geschwindigkeitssubtraktion geht stillschweigend davon aus, dass die Längen- und Zeitmessungen des hinterherfliegenden Raumschiffs dieselben sind wie meine eigenen. Im letzten Abschnitt haben wir dagegen gesehen, dass dies nicht der Fall ist. Die Längenmaßstäbe des Raumschiffs scheinen mir beispielsweise kürzer als meine eigenen, und seine Uhren langsamer. Zusammen kombinieren sich diese relativistischen Unterschiede der Raum- und Zeitmessung gerade so, dass das Unerwartete eintritt: Auch aus Sicht des hinterhereilenden Raumschiffes bewegt sich das betreffende Lichtsignal mit der Geschwindigkeit c = 299 792,458 Kilometer pro Sekunde.
Tatsächlich kombinieren sich die diversen relativistischen Effekte ganz allgemein so, dass das Prinzip der Konstanz der Lichtgeschwindigkeit gewährleistet bleibt: Für jeden Raumstationsbewohner (genauer gesagt: für jeden Inertialbeobachter) hat jedes Lichtsignal dieselbe, konstante Geschwindigkeit von c = 299 792,458 Kilometern pro Sekunde, unabhängig von der Geschwindigkeit der Lichtquelle.
Die Lichtgeschwindigkeit ist die einzige Geschwindigkeit, die in diesem Sinne beobachterunabhängig-absolut ist. Und ihre Sonderrolle in der Speziellen Relativitätstheorie zeigt sich noch in weiterer Hinsicht:
Erstens ist sie die absolute Höchstgeschwindigkeit für die Übertragung von Information, Materie und Energie. Kein Objekt, so stark man es auch beschleunigt, kann je die Lichtgeschwindigkeit erreichen (warum das so ist, wird im Abschnitt E = mc² erklärt).
Zweitens ist sie der allgegenwärtige Parameter in den Gleichungen der Speziellen Relativitätstheorie. Wie ausgeprägt ein gegebener relativistischer Effekt ist, der sich aus der Relativbewegung zweier Bezugssysteme ergibt, hängt entscheidend davon ab, wie groß diese Relativgeschwindigkeit im Vergleich zur Lichtgeschwindigkeit ist.