Special relativity / Elementary Tour part 4: The speed of light

On the previous pages, relativity reigned supreme. Although we usually think of lengths and times as absolute, they turned out to be observer-dependent. On this page, the shoe is on the other foot. Ordinarily, we think of velocities as relative, but one of them turns out to be absolute: the speed of light.

From our everyday experience, we’re used to adding or subtracting velocities. Imagine that you’re standing near a highway, watching the cars go by. Let’s say that there are two cars, side by side, each of them with a speed of 60 miles per hour:

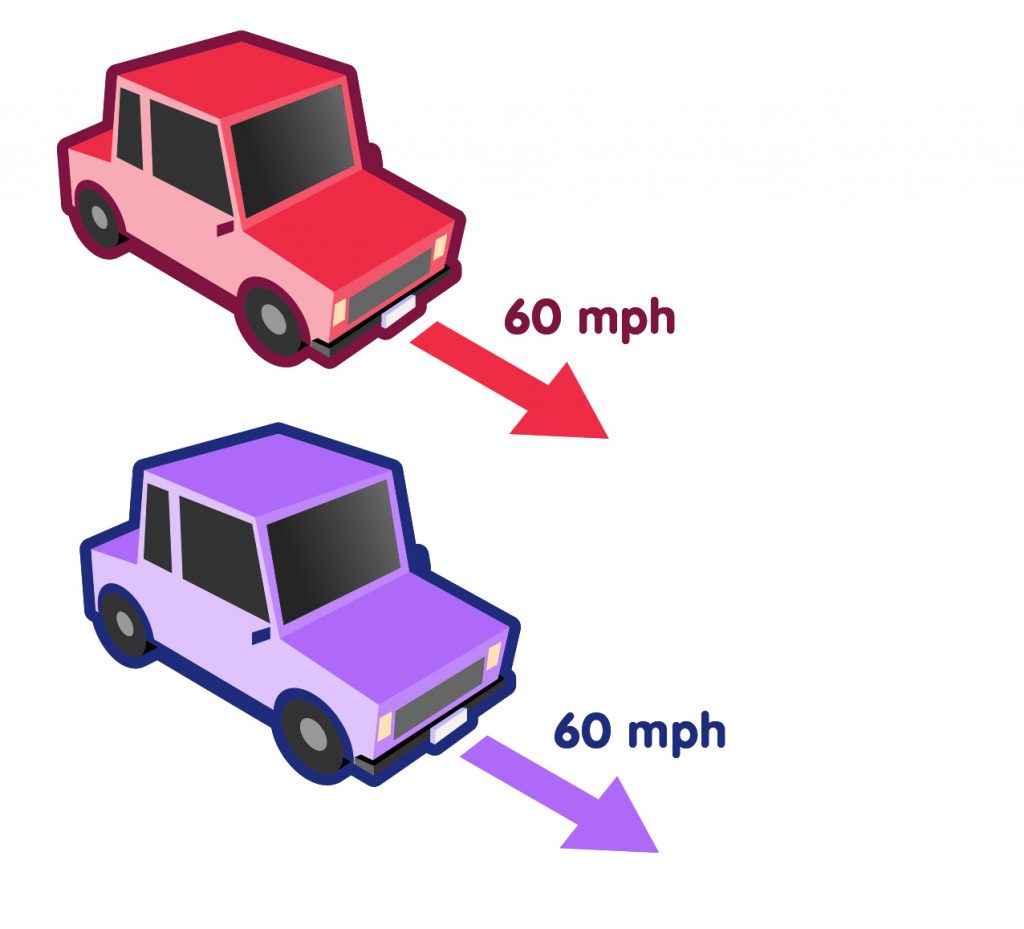
Two cars driving side by side, each with 60 mph

You would conclude (and rightly so) that from the point of view of each of the drivers, the other car does not move at all. If, on the other hand, one of the cars drove along at 80 miles per hour,

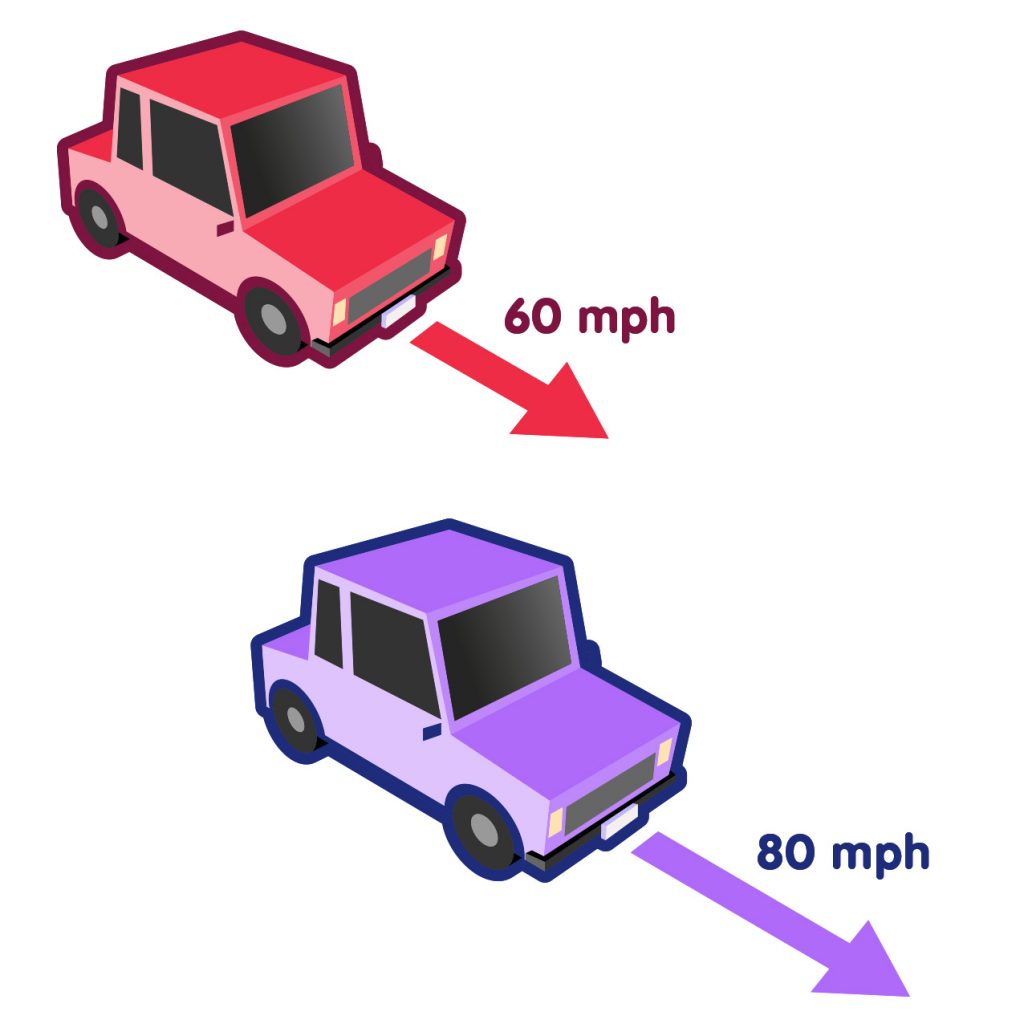
Two cars driving side by side, one with 80, the other with 60 mph

then the driver in the other vehicle would see it forge ahead with a speed of 20 miles per hour, relative to his own car. In both cases, speed is subtracted from speed to give relative speed: 60 minus 60 miles per hour gives a relative speed of zero miles per hour in the first case, and 80 minus 60 miles per hour gives 20 miles per hour in the second case.

For light, it would be natural to expect that one could similarly add and subtract velocities. Suppose that I measure a particular light signal’s speed, and find the usual value of 299,792.458 kilometres (186,000 miles) per second. If I see a fast spaceship chase right after that signal, moving at half the speed of light (c/2), I would expect that an observer on that spaceship would measure the speed of my light signal at merely c – c/2 = c/2, half the value that I measured.

Not so, according to special relativity! Simply subtracting speeds would only give the correct answer if the observer on that space-ship measured space and time, distance and duration in the same way that I do. As we have seen on the previous page, that’s not the case. From my point of view, for instance, the measuring rods on the speeding spaceship are shorter than my own, and its clocks run more slowly than mine. Taken together, all of these relativistic effects combine in precisely the right way to result in a surprising phenomenon: Even from the point of view of an observer on the speeding spaceship, my light signal moves with exactly the same speed, c = 299,792.458 kilometres per second.

This phenomenon is far from coincidental. In fact, it is a systematic feature of special relativity. All the different relativistic effects combine, quite generally, so that the following postulate holds true: For any observer on one of the space stations (for any inertial observer, in short), any light signal moves through empty space with the same constant speed, c = 299,792,458 kilometres per second, independent of the motion of the light source.

The speed of light is the only speed that is, in this sense, independent of the observer and thus absolute. It also plays the lead role in all of special relativity.

First of all, it defines the absolute speed limit for the transfer of energy, matter and information. No object, however strong the forces acting upon it, can ever be accelerated to light speed. (Some reasons why that is so are given in the section E = mc².)

Secondly, the speed of light c is a ubiquitous parameter in the equations of special relativity. If the relative speed v is small compared to c, so are the relativistic effects. With v close to c, the relativistic effects become prominent, but with speeds small compared to c, such as the speeds we encounter in everyday life, relativistic effects are almost unnoticable.

Previous part: The relativity of space and time

Next part: Spacetime

Tour index

Definitioner

time

It is a fact of life that not all events in our universe happen concurrently - instead, there is a certain order. Defining a time coordinate or defining time, the way physicists do it, is to define a prescription to associate with each event a number so as to reflect that order - if event B happens after event A, then the number associated with B should be larger than that associated with A. The first step of this definition is to construct a clock: Choose a simple process that repeats regularly. (What is "regular"? Luckily, in our universe, all elementary processes such as a swinging pendulum, the oscillations of atoms or of electronic circuits lead to the same concept of regularity.) As a second step, install a counter: A mechanism that, with every repetition of the chosen process, raises the count by one. With this definition, one can at least assign a time (the numerical value of the counter) to events happening at location of the clock. For events at different locations, an additional definition is necessary: One needs to define simultaneity. After all, the statement that some far-away event A happens at 12 o'clock is the same as saying that event A and "our clock counter shows 12:00:00" are simultaneous. The how and why of defining simultaneity - a centre-piece of Einstein's special theory of relativity - are described in the spotlight topic Defining "now". With all these preparations, physicists can, in principle, assign a time coordinate value ("a time") to any possible events, and describes how fast or how slow processes happen, compared to that time coordinate.

speed

An object's average speed is the distance it moves during a given period of time, divided by the length of the time interval. If you make the time interval infinitely small, the result is the object's speed at one particular moment in time. The notion of speed can be applied to waves in different ways; for instance, for a simple wave, the phase speed is the speed at which any given wave crest or wave propagates through space. See also the more general entry velocity.

speed of light

The speed at which light or, more generally, electromagnetic radiation propagates through space (especially: through empty space). Central quantity in special relativity: There, the constancy of the speed of light is a basic postulate: every observer (more precisely: every inertial observer) that measures the speed of light in vacuum obtains the same constant value, c=299,792,458 metres per second. Another important relativistic aspect of the speed of light is that it defines an absolute upper speed limit: In special relativity, nothing can move faster than light, and information or influence at most be transmitted at light-speed. In general relativity, the same law is in force locally: No object, no matter, no information can directly overtake or catch up with light (cf. causality). Basic information about the role of light speed in special relativity can be found in the chapter Special relativity of Elementary Einstein.

special relativity

Albert Einstein's theory of the fundamentals of space, time, and movement (but not gravity). For a brief introduction, check out the chapter Special relativity of Elementary Einstein. Selected aspects of special relativity are described in the category Special relativity of our Spotlights on relativity.

space

In a strict sense: Space as we know it from everyday life: the totality of all locations in which objects can sit, with three dimensions. In a more general sense used by mathematicians, all kinds of sets of points are spaces - a line for instance, which has but a single dimension, or a two-dimensional surface, but also higher-dimensional spaces. Also, in such more general spaces, geometry can be different from the standard Euclidean geometry taught in high schools - such spaces can be curved.

second

In the International System of units: the basic unit of time. Defined as a certain multiple of the oscillation period of electromagnetic radiation set free in a certain transition within the electron shell of atoms of the type Cesium-133.

relativistic

Models, effects or phenomena in which special relativity or general relativity play a crucial role are called relativistic. Examples are relativistic quantum field theories as theories based on special relativity, or the relativistic perihelion shift as a consequence of general relativity. In addition, conditions under which the difference between relativistic physics and ordinary, classical physics are especially pronounced, are also called relativistic. For instance, when material objects reach speeds close to speed of light, one talks of relativistic speeds, while speeds that are so small compared to light as to make relativistic effects undetectably small are non-relativistic.

point

Elementary "building block" of geometrical entities such as surfaces or more general spaces. For instance, a surface is the set of all its points, of all possible locations on the surface, and all geometrical objects in that surface are defined by the points that belong to them - for instance, a line on the surface is the set of (infinitely many) points.

relativistic (perihelion advance, relativistic)

For planetary orbits, there is a small difference between the predictions of Newtonian gravity and general relativity. For instance, in Newton's theory, the orbital curve of a lonely planet orbiting a star is an ellipse. In general relativity, it is a kind of rose or rhodonea curve. Such a curve is similar to an ellipse curve, which shifts a bit with each additional orbit. The shift can be defined by looking at the point which is closest to the sun (perihelion) on each orbit. The additional relativistic shift is, hence, called relativistic perihelion shift or relativistic perihelion advance. A picture can be seen on the page A planet goes astray in the chapter General relativity of Elementary Einstein.

observer

In the context of relativity, "observer" can mean two different things. Often, observer is synonymous with reference frame or (spacetime-)coordinate system: An observer in this sense is someone who assigns coordinates to everything that happens around him. In particular, all events are assigned space coordinate values and a time coordinate value. In the context of special relativity, it is often the case that when one talks about an observer, what is really meant is an inertial observer, corresponding to a special type of reference frame. On other occasions, the term is used in a more narrow sense - in those cases, an observer is someone sitting at a certain point in space and using the light signals reaching that location to construct an image of his surroundings. In the context of optical effects in relativity, for instance gravitational lensing, observer is usually meant in this way.

matter

In general relativity: All contents of spacetime that contribute to its curvature: particles, dust, gases, fluids, electromagnetic and other fields. In particle physics: All elementary particles with half-integer spin, such as electrons and quarks, as well as their composites such as protons and neutrons, in contrast with force particles.

light

Light in the strict sense of the word is electromagnetic radiation the human eye can detect, with wave-lengths between 400 and 700 nano metres. In relativity theory and in astronomy, the word is often used in a more general sense, encompassing all kinds of electromagnetic radiation. For instance, astronomers might talk about "infrared light" or "gamma light"; in this context, light in the stricter sense is referred to as "visible light". Within classical physics, the properties of light are governed by Maxwell's equations; in quantum physics, it turns out that light is a stream of energy packets called light quanta or photons. In the context of relativistic physics, light is of great interest, and for a number of reasons. First of all, the speed of light plays a central role in both special and general relativity. Also, there are a number of interesting effects in general relativity which are associated with the propagation of light, namely deflection, the Shapiro effect and the gravitational redshift.

light speed

See speed of light.

lead

Chemical element with the symbol Pb; each lead nucleus contains 82 protons. Lead nuclei, stripped of their electrons, are among the types of heavy ions which are brought into collision in particle accelerators such as the Relativistic Heavy Ion Collider in order to recreate the state of matter in the early universe shortly after the big bang.

inertial observer

An inertial reference frame is a reference frame in which the first law of classical mechanics holds: A body on which no external forces act either remains at rest or moves with constant speed along a straight path. An inertial observer is an observer that is at rest with respect to an inertial reference frame. In the context of relativity, an inertial reference frame is one that drifts in gravity-free space without undergoing rotation or being accelerated.

Inertial reference frames play a central role in special relativity: the basic postulates of that theory are the relativity principle (which holds that the laws of physics are the same in all inertial reference frames - no such frame is special, in this sense) and the postulate that the speed of light has the same value for every inertial observer.

In general relativity, there are no real inertial observers, however, by what's called the equivalence principle, the laws of physics for an observer that is in free fall and performs his measurements only in his direct neighbourhood (and only over a limited period of time), the laws of physics are approximately the same as for an inertial observer.

energy

Physical quantity with the special property that, in physical processes, energy is neither destroyed nor created, simply transformed from one form of energy to another. Some of the different forms of energy that are defined separately are kinetic energy, thermal energy and the energy carried by electromagnetic radiation. Processes that transform one form of energy into another take place in all machines we use in everyday life, from the engine of a subway train (electrical energy into kinetic energy of the train) to an electric blanket (electrical energy into thermal energy). One important consequence of special relativity is that energy and mass are completely equivalent - two different ways to define what is, on closer inspection, one and the same physical quantity. See the keyword equivalence between mass and energy.

Special relativity / Elementary Tour part 4: The speed of light

Further Articles

Tag Cloud