Wellen in Bewegung: der Dopplereffekt

Wie sich Bewegung auf Wellen (oder andere periodische Signale) auswirkt – in der klassischen Physik und in der Speziellen Relativitätstheorie

Ein Artikel von Markus Pössel

Die Frequenz eines wellenähnlichen Signals wie Schall oder Licht ist abhängig von der Bewegung des Senders und des Empängers. Dieses Phänomen ist unter dem Namen Dopplereffekt bekannt, benannt nach dem österreichischen Physiker und Mathematiker Christian Doppler (1803-1853), der ihn vorhersagte. Einige der Erscheinungsformen des Effekts kennen wir aus dem Alltag: Wenn die Sirene eines Feuerwehrfahrzeugs schlagartig die Tonhöhe ändert, wenn der Wagen an uns vorbeifährt, ist das ein hörbares Beispiel für den Dopplereffekt. Auch in der Astronomie hat der Dopplereffekt wichtige Anwendungen – beispielsweise bei der Suche nach Planeten um andere Sterne. Grund genug, einen genaueren Blick auf diesen Effekt zu werfen und zu erkunden, wie es zu dieser Frequenzveränderung kommt.

Ausgesendete und empfangene Pulse

Beginnen wir mit dem einfachen Versuchsaufbau, den die folgende Animation zeigt. Auf der rechten Seite (rot) sehen wir einen Sender, der eine regelmäßige Folge von Pulsen aussendet. Auf der linken Seite befindet sich ein Empfänger (blau). Die Pulse selbst sind rot dargestellt und bewegen sich alle mit der gleichen Geschwindigkeit von rechts nach links. Jedes Mal, wenn der Sender einen neuen Puls sendet, leuchtet das Blinklicht am Sender auf. Entsprechend blinkt die Statusanzeige am Empfänger immer dann auf, wenn gerade ein Puls angekommen ist.

Beobachtet man zunächst das blinkende Licht am Detektor und dann das des Senders, dann sieht man, dass sie genau im gleichen Rhythmus aufleuchten – mit anderen Worten: Zwischen der Aussendung zweier aufeinander folgender Pulse am Sender vergeht genauso viel Zeit wie zwischen dem Empfang zweier aufeinanderfolgender Pulse.

Anders ausgedrückt: Die Frequenz, mit der die Pulse ausgesandt werden (ein Maß für die Anzahl der in einer gegebenen Zeitspanne ausgesandten Pulse) ist gleich der Frequenz, mit der sie empfangen werden.

Wenn die Quelle sich nähert

Als nächstes betrachen wir eine leicht abgeänderte Situation, in der sich die Quelle auf den Detektor zu bewegt. Wir nehmen an, dass sich die Quelle langsamer bewegt als die Pulse und dass die Pulse mit der gleichen Frequenz ausgesendet werden wie in der ersten Animation. Das Ergebnis ist hier zu sehen:

Der Abstand zweier aufeinander folgender Pulse ist in dieser Situation geringer als im ersten Beispiel, wo Sender und Empfänger relativ zueinander in Ruhe waren. Folglich kommen die Pulse beim Empfänger in einer schnelleren Folge an. Vergleicht man die Rate des Blinklichts des Senders mit der am Empfänger, so erkennt man, dass die Anzeige des Empfängers schneller blinkt.

Konkret auf das obige Beispiel bezogen: Der Sender bewegt sich in dieser Anordnung mit einem Drittel der Pulsgeschwindigkeit nach links. In der gleichen Zeitspanne, in der der Empfänger zwei Pulse aussendet, kommen drei Pulse beim Empfänger an. Mit anderen Worten: Die Frequenz, mit der die Pulse empfangen werden, ist 3/2=1,5 mal so groß wie die Frequenz, mit der sie gesendet werden. Die Frequenz hat sich verschoben, weshalb der Dopplereffekt oft auch Dopplerverschiebung genannt wird.

Wie kommt es dazu? Lassen Sie uns zurück zum Fall des unbewegten Senders gehen. Hier ist eine Momentaufnahme des Senders, wie er gerade einen Puls ausschickt:

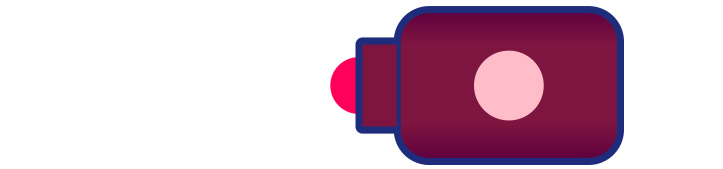
Nachdem ein bestimmtes Zeitinterval T vergangen ist, sendet der Sender einen zweiten Puls aus, wie im folgenden Bild zu sehen. In der Zwischenzeit hat sich der erste Puls um die Strecke d nach links bewegt:

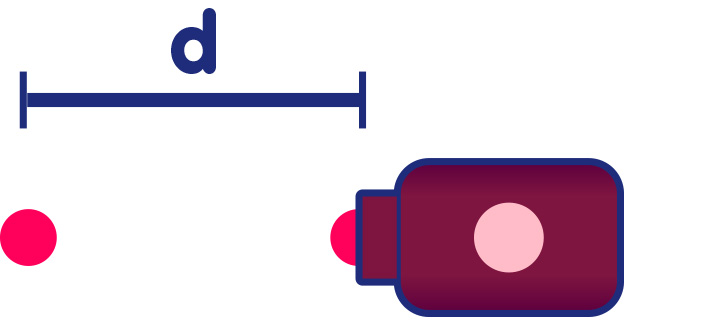
Der räumliche Abstand d bestimmt den zeitlichen Abstand, in dem die beiden Pulse beim Empfänger eintreffen. Alle Pulse bewegen sich mit der gleichen Geschwindigkeit fort, und die Zeit zwischen zwei Ankünften ist gerade die Zeit, die der zweite Puls benötigt, um die Distanz d zurückzulegen. Je größer d ist, desto mehr Zeit vergeht zwischen den Ankünften zweier aufeinanderfolgender Pulse. Je größer der Abstand aufeinanderfolgender Pulse, desto niedriger ist die Frequenz der Pulsankünfte. Sind die Pulse durch einen großen Abstand d getrennt, so kommen in einer gegebenen Zeit vergleichsweise wenige Pulse beim Empfänger an.

So weit, so gut. Aber was, wenn der Sender sich bewegt? Hier ist wieder eine Momentaufnahme des sich bewegenden Senders, der gerade einen Puls aussendet:

Nachdem das gleiche Zeitinterval T vergangen ist, stößt der Sender erneut einen zweiten Puls aus. In der Zwischenzeit hat sich der erste Puls wieder um die Distanz d nach links bewegt. Aber in diesem Fall ist er nicht der Einzige, der sich bewegt hat. Der Sender selbst hat sich um eine bestimmte Strecke D nach links bewegt, wie im folgenden Bild dargestellt ist:

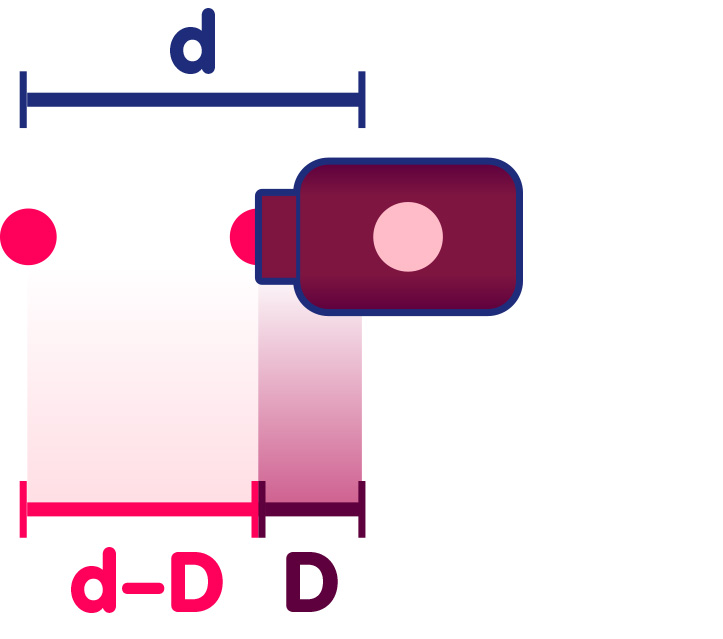
Aufgrund der Bewegung des Senders ist der Abstand zweier aufeinanderfolgender Pulse nun nicht mehr d, sondern d-D. Wenn aber der Abstand zwischen aufeinanderfolgenden Pulsen geringer ist, dann vergeht freilich auch weniger Zeit zwischen der Ankunft des ersten Pulses am Detektor und der Ankunft des zweiten! Anders ausgedrückt: Die Frequenz, mit der die Pulse beim Empfänger ankommen, ist höher.

Das ist unser erstes Beispiel für den Dopplereffekt: Bewegt sich der Sender zum Empfänger hin, so ist die Frequenz, mit der die Pulse beim Empfänger eintreffen, größer als die Frequenz, mit der sie vom Sender ausgesandt werden.

Wenn sich die Quelle entfernt

Was passiert, wenn sich die Quelle nicht auf den Empfänger zu, sondern von ihm wegbewegt? Das zeigt die folgende Animation:

Dieses Mal leuchtet die Blinklicht des Empfängers ein bisschen langsamer auf als das des Senders: Die Frequenz, mit der die Pulse empfangen werden, ist geringer als die der gesendeten Pulse. In diesem konkreten Beispiel bewegt sich die Quelle mit einem Drittel der Geschwindigkeit, mit der die Pulse nach links laufen, nach rechts. In der Zeit, die der Empfänger benötigt, um vier Pulse auszusenden, erreichen drei Pulse den Empfänger.

Was hier passiert, lässt sich genauso verstehen wie oben. Hier haben wir eine Momentaufnahme einer sich nach rechts bewegenden Quelle gegeben, die sich gerade anschickt, einen Puls nach links auszusenden:

Nach der Zeit T schickt die Quelle einen zweiten Puls auf die Reise. In der Zwischenzeit hat sich der erste Puls wiederum um die Distanz d nach links bewegt. Aber zusätzlich hat sich auch die Quelle bewegt, und zwar um die Strecke D nach rechts:

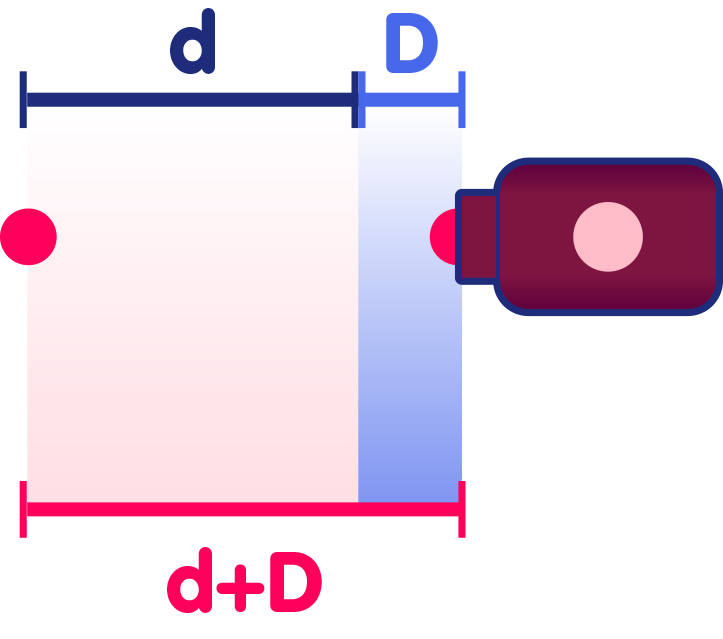
Folglich ist der Abstand zwischen zwei aufeinanderfolgender Puls in diesem Falle größer als bei einer ruhenden Quelle. Er beträgt nicht nur d sondern d+D. Aber ein größerer Abstand bedeutet, dass die Pulse weniger häufig beim Empfänger ankommen – zwischen zwei Pulsen liegt ein größeres Zeitintervall als im Falle einer ruhenden Quelle. Das ist unser zweites Beispiel für den Dopplereffekt: Entfernt sich der Sender vom Empfänger, dann ist die Frequenz, mit der die Pulse beim Empfänger ankommen, geringer als die Frequenz, mit der sie vom Sender ausgesandt werden.

Von Pulsen zu Wellen

Stellen Sie sich jetzt bitte vor, dass unser Sender anstelle einzelner Pulse eine einfache Welle emittiert: ein Muster aus Maxima und Minima (Wellenbergen und Tälern) einer physikalischen Größe, die in perfekter Regelmäßigkeit einander folgen und mit einer konstanten Geschwindigkeit durch den Raum laufen (wie hier durch den Pfeil angedeutet):

Zum Beispiel könnte unser Sender eine Schallwelle emittieren, in der die Wellenberge und Täler jeweils Regionen mit maximalen bzw. minimalen Luftdruck entsprechen. Solch eine Schallwelle würde mit einer konstanten Geschwindigkeit, der Schallgeschwindigkeit, durch die Luft wandern. Alternativ könnte unser Sender eine elektromagnetische Welle aussenden, in der die Wellenberge und Täler den Minima und Maxima einer weniger anschaulichen physikalischen Größe entsprechen, nämlich des elektrischen oder, alternativ, des Magnetfelds.

Entscheidend ist, dass sich all das, was wir uns für die Aussendung und den Empfang aufeinanderfolgender Pulse überlegt haben, eins zu eins auf Aussendung und den Empfang aufeinander folgender Wellenberge (oder Wellentäler) übertragen lässt: Bewegt sich die Quelle auf den Empfänger zu, so platziert sie jeden weiteren ausgesandten Wellenberg etwas näher an seinem Vorgänger als bei einer ruhenden Quelle. Auf diese Weise gelangen wir zu der bekanntesten Version des Dopplereffekts, der Wellen betrifft: Bewegt sich die Quelle einer Welle auf einen Empfänger zu, so ist die Frequenz, mit der die Wellen empfangen werden, höher als die Frequenz, mit der sie losgeschickt wurden. Umgekehrt ist die Frequenz, mit der die Wellen empfangen werden, bei sich entfernenden Quellen niedriger als bei ruhenden.

Bei Schallwellen dürften viele Leser den Dopplereffekt bereits direkt gehört haben. Bei diesen Wellen entsprechen höhere Frequenzen höheren Tönen und tiefere Frequenzen tieferen Tönen. Wer jemals an einer Straße gestanden und erlebt hat, wie ein Feuerwehr- oder Polizeiwagen mit Blaulicht und Martinshorn vorbeifährt, weiß: Während der Wagen noch auf einen zu fährt ist der Ton des Signalhorns höher; wenn der Wagen vorbeifährt wird er abrupt tiefer. Hier ist ein Klangbeispiel:

Abspielen [MP3, 258 kB], Download [ZIP, 184kB]

(Würde der Einsatzwagen direkt durch uns hindurch fahren, dann wäre der Ton hoch, solange der Wagen auf uns zu fährt, und würde in dem Moment, wo der Wagen durch uns hindurch fährt, abrupt nach unten springen. Da wirkliche Einsatzwagen [hoffentlich!] an uns vorbei anstatt durch uns hindurch fahren, ist der Übergang dort etwas allmählicher.)

Bei einfachen Lichtwellen besteht ein direkter Zusammenhang zwischen der Frequenz und der Farbe des Lichts. Die niedrigste Frequenz im Bereich des sichtbaren Lichts hat dabei das rote Licht. Zu immer höheren Frequenzen hin wird das Licht gelb, grün, blau und schließlich violett, wie hier schematisch dargestellt – alle Farben des Spektrums:

Licht einer Quelle, die sich auf den Beobachter zu bewegt, wird zu höheren Frequenzen, anders gesagt: in Richtung des blau-violetten Endes des Spektrums verschoben. Daher werden solche Verschiebungen zu höheren Frequenzen hin auch Blauverschiebung genannt. Umgekehrt wird Licht einer sich von dem Beobachter entfernenden Quelle rotverschoben. In der Astronomie stellt dieser Effekt ein wichtiges Werkzeug dar, um die Bewegung von Sternen oder anderen Himmelsobjekten zu ermitteln.

Die Begriffe Rot- und Blauverschiebung werden auch für andere Wellenphänomene gebraucht, nicht nur für sichtbares Licht. Ganz allgemein werden Verschiebungen in Richtung höherer Frequenzen Blauverschiebungen und solche zu niedrigeren Frequenzen hin Rotverschiebungen genannt. Das gilt auch für Wellen, die sich überhaupt nicht direkt mit einer Farbe in Verbindung bringen lassen, wie zum Beispiel Radio- oder Gravitationswellen.

(Der Sprachgebrauch kann dabei etwas verwirrend sein. Beispielsweise bezeichnet man auch Infrarotstrahlung, die zu niedrigeren Frequenzen hin verschoben wird, als rotverschoben, da „rotverschoben“ in diesem Zusammenhang eben nur ein Kürzel für „zu niedrigeren Frequenzen hin verschoben“ ist. Aber Infrarotstrahlung liegt im Spektrum bei noch niedrigeren Frequenzen als sichtbares, rotes Licht; eine Verschiebung zum sichtbaren roten Licht hin wäre für diese Strahlung eine Verschiebung hin zu höheren Frequenzen. Davon sollte man sich nicht verwirren lassen; der Sprachgebrauch ist immer: „rotverschoben“ = „zu niedrigeren Frequenzen hin verschoben“ und „blauverschoben“ = „zu höheren Frequenzen hin verschoben“.)

Der Dopplereffekt in zwei Dimensionen

Bis jetzt haben wir nur Pulse bzw. Wellen betrachtet, die in eine bestimmte Richtung ausgesandt wurden. Dabei ist es zum Verständnis des Dopplereffekts durchaus nützlich, eine Situation zu betrachten, in der Wellen in alle Richtungen gleichzeitig ausgesandt werden. Aus Gründen der Anschaulichkeit beschränke ich mich hier auf zwei Dimensionen und untersuche eine Welle, die in einer Ebene ausgesendet wird:

Zum Beispiel könnte die Quelle (in rot) jemand sein, der über einem See schwebt und einen Stempel periodisch hoch und runter ins Wasser bewegt. Die sich ausbreitenden hellroten Ringe wären dann die Kämme (Berge) der Wasserwellen, die sich auf der Oberfläche nach außen hin fortpflanzen. Alternativ könnte die Quelle eine Lichtquelle sein, die Licht in alle Richtungen aussendet. In diesem Falle könnten die roten Linien die Maxima einer elektromagnetischen Welle sein. Bei einer Quelle, die Schallwellen aussendet, könnten die roten Ringe Zonen maximalen Luftdrucks sein.

Die folgende Animation zeigt, was passiert, wenn die Quelle sich nicht in Ruhe befindet, sondern sich nach links bewegt (wie in den vorangehenden Animationen mit einem Drittel der Ausbreitungsgeschwindigkeit der Welle).

Wie deutlich zu erkennen ist, liegt der Mittelpunkt jedes neuen ringförmigen Wellenkamms ein Stückchen links von dem seines Vorgängers. Deshalb können wir nun alle Facetten des Dopplereffektes auf einmal sehen: Die Wellenberge, die sich direkt nach links ausbreiten, sind dichter zusammengedrängt, was einer höheren Frequenz der Welle entspricht. Ein Beobachter, der diese Welle empfängt, sieht, dass sich die Quelle auf ihn zu bewegt und bemerkt die entsprechende Blauverschiebung der Welle. Umgekehrt liegen die Wellenberge, die sich direkt nach rechts bewegen, weiter auseinander. Das entspricht der Rotverschiebung, wie sie ein Beobachter misst, von dem sich die Welle weg bewegt.

Was passiert, wenn sich die Quelle genauso schnell bewegt wie das Signal selbst? In diesem Fall werden die Signale vor der Quelle zusammengedrängt und erreichen den Beobachter dann alle zur selben Zeit. Auch davon werden viele Leser eine Variante kennen: Den Überschallknall, der entsteht, wenn ein Flugzeug die Schallgeschwindigkeit erreicht (und diese anschließend überschreitet). Der Knall selbst ist eine Ansammlung von dicht gedrängten Schallwellenmaxima, die sich vor dem Flugzeug zusammendrängen.

Was, wenn der Empfänger sich bewegt?

Bislang haben wir nur sich bewegende Quellen berücksichtigt. Eine nähere Betrachtung zeigt, dass sich auch in dem Falle, dass sich nicht die Quelle, sondern der Empfänger bewegt, ein entsprechender Dopplereffekt ergibt. Hier ist ein Beispiel:

Beobachtet man wieder die blinkenden Indikatorlampen, stellt man auch hier eine Blauverschiebung fest: die Pulsfrequenz, die beim Empfänger gemessen wird, ist etwas höher als die, mit der die Pulse ausgesendet wurden. In diesem Fall sind zwar die Abstände zwischen aufeinanderfolgenden Pulsen genau so lang wie in dem Falle, in dem sich weder Empfänger noch Quelle bewegen. Dennoch gibt es eine Frequenzverschiebung: Da sich der Empfänger auf jeden Puls zu bewegt, wird die Zeit, bis sich Puls und Empfänger treffen, jeweils verkürzt.

In dieser konkreten Animation, in der sich der Empfänger mit einem Drittel der Pulsgeschwindigkeit auf die Quelle zu bewegt, werden am Empfänger vier Pulse in der Zeit empfangen, die die Quelle benötigt, um drei Pulse auf den Weg zu schicken.

Bewegt sich der Empfänger von der Quelle weg, dann muss jeder Puls in ähnlicher Weise eine etwas längere Distanz zurücklegen als sein Vorgänger, um den Empfänger zu erreichen. Das Ergebnis ist in dieser Animation dargestellt:

Wiederum bewegt sich der Empfänger hier mit einem Drittel der Pulsgeschwindigkeit, in diesem Fall jedoch von der Quelle weg. In der Zeit, die die Quelle benötigt um drei Pulse abzugeben, kommen nur zwei Pulse beim Empfänger an – die Pulsfrequenz ist beim Empfänger auf 66,67 Prozent der ursprünglichen Pulsfrequenz der Quelle „rotverschoben“.

Der Dopplereffekt in der Speziellen Relativitätstheorie

Alle bisherigen Argumente basierten auf der klassischen Physik. Sobald man die Spezielle Relativitätstheorie ins Spiel bringt, wird als weiterer Effekt die Zeitdilatation wichtig. Nehmen wir an, dass der Beobachter, der am Empfänger sitzt und das Eintreffen der Pulse registriert, einer der Standardbeobachter der Speziellen Relativitätstheorie, ein sogenannter Inertialbeobachter (z. B. ein Beobachter, der frei im Raum schwebt, weit weg von allen signifikanten Gravitationsquellen). Bestimmt unser Beobachter die Zeitdauern von Vorgängen, die sich an der Quelle der Pulse ereignen, dann wird er im Vergleich mit einem Beobachter direkt an der Quelle längere Werte für die Zeitdauern erhalten, die Vorgänge also verlangsamt wahrnehmen.

Führen wir umgekehrt einen inertialen Beobachter ein, der sich relativ zur Quelle in Ruhe befindet, und lassen ihn einen sich bewegenden Empfänger betrachten, so stellt der Beobachter fest, dass die Uhr des Empfängers (die benutzt wird um festzustellen, wie schnell die Pulse beim Empfänger ankommen) langsamer geht als seine eigene.

Die Kombination aus Zeitdilatation und den schon geschilderten Umständen des klassischen Dopplereffekts (durch obige Animationen veranschaulicht) ergibt den relativistischen Dopplereffekt.

Der relativistische Dopplereffekt und die Relativität der Bewegung

Wenn Sie die Beispiele genau verfolgt haben, so haben Sie möglicherweise festgestellt, dass die klassischen Dopplereffekte für eine sich bewegende Quelle und einen sich bewegenden Empfänger unterschiedlich sind. In unseren Beispielen war Quelle bzw. Empfänger jeweils mit einem Drittel der Signalgeschwindigkeit bewegt. Dennoch war die Frequenzverschiebung nicht die gleiche: Näherte sich die Quelle mit einem Drittel der Pulsgeschwindigkeit dem Empfänger, dann war die Frequenz des Pulsempfangs 1,5 mal so groß wie die Frequenz der Pulsaussendung durch die Quelle – während derjenigen Zeitspanne, in der von der Quelle zwei neue Pulse ausgesandt wurden, kamen beim Empfänger drei Pulse an. Bewegte sich dagegen der Empfänger auf die Quelle zu, war die Pulsfrequenz beim Empfänger nur 1 1/3 (also 1,33333…) mal so groß wie die Frequenz bei der Quelle – während die Quelle drei Pulse aussendet, kommen vier Pulse beim Empfänger an.

Für Pulse oder Wellen, die sich in einem Medium ausbreiten, etwa Schallwellen in Luft, ist es einfach, festzustellen, wer sich relativ zum Medium bewegt, Quelle oder Empfänger. Aber was ist mit elektromagnetischen Wellen wie beispielsweise Licht? Deren Ausbreitung ist in der modernen Physik nicht mit einem bestimmten Medium verknüpft. Sie wird direkt von einem physikalischem Gesetz bestimmt (den Maxwellgleichungen um genau zu sein). Ist also der Dopplereffekt für Licht unterschiedlich, abhängig davon ob sich die Quelle oder der Empfänger bewegt?

Wäre dies der Fall, dann ließe sich absolute Bewegung definieren – allein aus den Gesetzen der Physik (in diesem Falle: der Lichtausbreitung) ließe sich bestimmen, ob sich die Quelle, der Empfänger oder irgendein anderes Objekt bewegt oder nicht. Das stünde im direkten Gegensatz zur Speziellen Relativitätstheorie, in der es keine absolute Bewegung gibt und in der die Gesetze der Physik für relativ zueinander bewegte (Inertial-)Beobachter die gleichen sind.

Die Lösung? Wie bereits erwähnt unterscheidet sich der relativistische Dopplereffekt von seinem klassischen Gegenstück. Er muss die relativistische Zeitdilatation berücksichtigt, und wie sich herausstellt, verbinden sich die Zeitdilatation und der klassische Dopplereffekt genau so, dass für Lichtwellen (oder andere lichtschnelle Signale) kein Unterschied besteht, ob sich nun die Quelle oder der Empfänger bewegt. Im relativistischen Dopplereffekt für Licht zählt allein die Relativbewegung der Quelle und des Empfängers.

Der transversale Dopplereffekt

Die Spezielle Relativitätstheorie fügt dem Dopplereffekt eine weitere Facette hinzu. In der klassische Physik gibt es nur dann einen Dopplereffekt, wenn ihre Bewegung Empfänger oder Quelle zumindest ein wenig aufeinander zu oder voneinander weg führt. In der Speziellen Relativitätstheorie dagegen gibt es selbst dort, wo Empfänger oder Quelle seitwärts aneinander vorbeifliegen, einen Rest an Dopplereffekt.

Hier ist diese Situation dargestellt: Stellen Sie sich vor, dass Sie eine sich bewegende Quelle beobachten. Weder entfernt sich die Quelle in dem dargestellten Moment von ihnen, noch bewegt sie sich auf Sie zu – sie bewegt sich genau seitwärts (oder, um es anders auszudrücken, sie bewegt sich exakt in einem rechten Winkel zu Ihrer Blickrichtung):

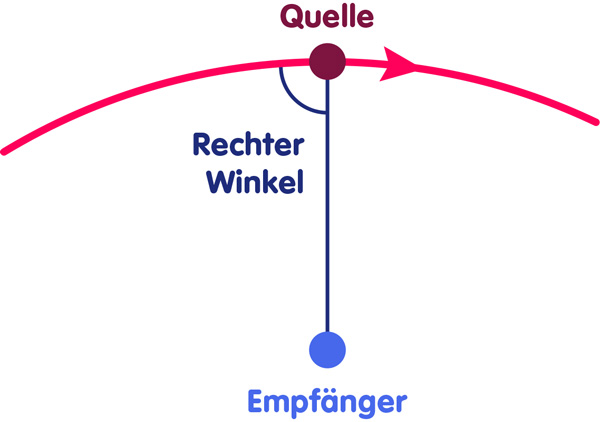
Sie werden immer noch einen relativistischen Dopplereffekt feststellen. Die Frequenz von welcher Art Welle auch immer die Quelle in Ihre Richtung sendet wird niedriger sein als wenn die Quelle sich in Ruhe befinden würde.

Warum ist dies so? Erinnern Sie sich daran, dass der relativistische Dopplereffekt einen Kombination aus klassischem Dopplereffekt und relativistischer Zeitdilatation ist. Sogar in einer Situation, in welcher der klassische Dopplereffekt überhaupt keinen Beitrag leistet – Seitwärtsbewegung -, ist da immer noch die Zeitdilatation. Sogar für eine Quelle, die sich seitwärts zu Ihnen bewegt („transversale Bewegung“) erscheinen alle Prozesse langsamer – auch das Aussenden der Abfolge von Wellenbergen und -tälern. Dies ist der transversale Dopplereffekt – wie gesagt: eine Erscheinungsform der Zeitdilatation.

Weitere Informationen