Ein Leitstern durch die Dunkelheit der Natur: Symmetrie in der Physik

Im letzten Jahrhundert nahmen Symmetrien einen zentralen Platz im Verständnis der theoretischen Physiker vom Verständnis der Realität ein.

Ein Artikel von Mattia Cesaro

Ausgehend von phänomenologischen Beobachtungen, die mit Schönheit und Perfektion bei den frühen Griechen verbunden waren, hat sich das Konzept der Symmetrie im Laufe der Zeit weiterentwickelt und wurde mathematisch formalisiert, sodass es heute ein grundlegendes Leitprinzip bei der Entwicklung moderner physikalischer Theorien darstellt. In diesem Artikel werde ich den Begriff der Symmetrie in der Physik erkunden, mich mit der starken Verbindung zwischen Symmetrien und Erhaltungssätzen befassen und auf die Bedeutung von Symmetrien für unser Verständnis der Natur eingehen.

Symmetrien physikalischer Gesetze

Das Konzept der Symmetrie in der Physik ähnelt stark dem intuitiven Verständnis, das wir aus unserem Alltag haben. Nehmen wir einen Gegenstand und wenden eine Operation auf ihn an (z. B. ihn bewegen, drehen usw.): Wenn er sich nicht verändert, bezeichnen wir die Operation als eine Symmetrie des Gegenstands und sagen, dass sie den Gegenstand unverändert lässt. Eines der typischen Beispiele ist die Rotationssymmetrie einer Kugel: Die Kugel sieht nach einer Drehung um einen beliebigen Winkel im Raum immer noch wie sie selbst aus. Natürlich weist auch ein Quadrat eine gewisse Symmetrie auf: Wenn wir es drehen, diesmal jedoch genau um 90 Grad und nicht um einen beliebigen Winkel, sieht es immer noch wie dasselbe Quadrat aus, so als ob diese Drehung nicht stattgefunden hätte.

Diese Situation lässt sich verallgemeinern. Neben den Symmetrien konkreter Einzelobjekte interessieren uns oft auch die Symmetrien ganzer Systeme und sogar der physikalischen Gesetze selbst, da sie Muster und Regelmäßigkeiten des Universums zusammenfassen, die nicht von dem konkreten Phänomen abhängen, das wir untersuchen. Aber was bedeutet es, dass ein physikalisches Gesetz eine Symmetrie besitzt? Es bedeutet, dass es eine Reihe von Operationen gibt, die wir an dem zu analysierenden System durchführen können, ohne dass sich die physikalischen Gesetze ändern (oder besser gesagt, ihre mathematische Form), denen das System gehorcht. Wir könnten uns beispielsweise fragen, was mit dem Ergebnis eines Experiments passieren könnte, wenn wir es hier und jetzt in unserem Labor durchführen oder wenn wir dasselbe Labor um einige Meter in eine Richtung verschieben (wobei alle anderen Bedingungen gleich bleiben). Oder wenn wir das Labor aus einem anderen Blickwinkel betrachten. Wenn wir das Experiment heute oder morgen durchführen. Die Antwort lautet: nichts. Solche Transformationen werden als Verschiebungen im Raum, Drehungen im Raum und Zeitverschiebungen bezeichnet, und die physikalischen Gesetze, die solche Experimente beschreiben, bleiben davon unberührt; die Transformationen stellen Symmetrien der physikalischen Gesetze dar, denen das System unterliegt.

Versuchen wir, etwas formeller zu sein. Fast alle Informationen (mit Ausnahme der Anfangsbedingungen) über die Dynamik des Systems, nämlich seine Entwicklung im Laufe der Zeit und die es bestimmenden Gesetze, sind auf elegante Weise in einem einzigen mathematischen Objekt, der sogenannten Lagrange-Funktion, kodiert. Bei einfachen Systemen wie einer Masse im freien Fall oder einer an einer Feder befestigten Masse entspricht die Lagrange-Funktion einfach der Differenz zwischen der kinetischen und der potenziellen Energie des Systems; bei komplizierteren Systemen wird er zu einem komplexeren Gebilde.

 Wir können alle möglichen Transformationen auf dieses Objekt anwenden, und wann immer die von uns angewandte Transformation eine Symmetrie des Systems ist, bleibt die Lagrange-Funktion unverändert. Diese Aussage ist nicht ganz korrekt, da sich die Lagrange-Funktion je nach konkretem Fall auch um einen (für die Dynamik des Systems unerheblichen) totalen Ableitungsterm ändern kann. Im weiteren Verlauf dieses Aufsatzes wollen wir uns dennoch auf den einfachsten Fall einer unveränderten Lagrange-Funktion beschränken. 

Dies präzisiert die weiter oben beschriebene intuitive Vorstellung von der Symmetrie eines Systems.

Noether-Theorem und Erhaltungssätze

Wir können nun die tiefe Verbindung zwischen Symmetrien und Erhaltungssätzen diskutieren, die 1915 von der deutschen Mathematikerin Emmy Noether entdeckt wurde. Erhaltungsgrößen werden so genannt, weil sie sich mit der Zeit nicht ändern: Sie sind am Anfang und am Ende eines Prozesses gleich und werden manchmal auch als Erhaltungsgrößen bezeichnet.

 Ein sehr bekanntes Beispiel, das für ein isoliertes System (d. h. ein System ohne Austausch mit der Umgebung) typisch ist, ist die Energie: Im Laufe des Prozesses kann diese zwar ihre Form ändern, beispielsweise von Licht zu Wärme, aber die Gesamtenergie im System bleibt unverändert. Erhaltungsgrößen sind äußerst nützlich, um die Dynamik eines Systems zu berechnen, was sonst oft zu einer sehr komplexen Analyse führen würde, aber sie sind nicht immer leicht a priori zu finden.

 Das bemerkenswerte Ergebnis, das Emmy Noether bewiesen hat, lautet wie folgt:

Wann immer das System eine kontinuierliche Symmetrie aufweist, gibt es eine Erhaltungsgröße, die mit dieser spezifischen Symmetrie verbunden und für sie charakteristisch ist und die wir explizit bestimmen können.

Hier bedeutet „kontinuierlich” einfach, dass die Anwendung der Transformation in eine Vielzahl sehr kleiner Transformationen zerlegt werden kann. Dies steht im Gegensatz zu diskreten Symmetrien wie einer Spiegelung, bei denen dies nicht möglich ist.

Betrachten wir beispielsweise erneut die beiden bekannten Rotationssymmetrien der Kugel und des Quadrats (Abbildung 1 oben): Nur die Symmetrie der Kugel ist kontinuierlich, während die des Quadrats diskret ist, da das Quadrat bei einer beliebigen winzigen Drehung nicht mehr wie zuvor aussieht.

Der Satz hat tiefgreifende Auswirkungen auf die Art und Weise, wie wir die Physik der uns umgebenden Welt interpretieren. Betrachten wir noch einmal die Laborexperimente und die Symmetrien der physikalischen Gesetze. Da die Physik der Experimente in zwei voneinander entfernten Laboren gleich ist, bleibt nach dem Noether-Satz der Impuls erhalten. Diese Größe ist definiert als die Gesamtheit der am Experiment beteiligten Massen multipliziert mit ihren jeweiligen Geschwindigkeiten. Das bedeutet beispielsweise, dass die Art und Weise, wie zwei Billardkugeln (wenn wir die Reibung vernachlässigen) auf dem Tisch elastisch kollidieren, nach dem Theorem als Folge der Ortsunabhängigkeit der physikalischen Gesetze verstanden werden kann.

Da die Physik in einem gedrehten (nicht in einem rotierenden!) Laboratorium dieselbe ist, bleibt gemäß dem Noether-Theorem auch der Drehimpuls, das rotierende Analogon zum linearen Impuls, erhalten. Daher lässt sich die Erhaltung des Drehimpulses aus der Tatsache ableiten, dass die Gesetze der Physik nicht vom Winkel abhängen, aus dem wir die Dinge messen. Ein berühmtes Beispiel hierfür ist eine Eiskunstläuferin, die sich je nachdem, ob sie ihre Arme ausstreckt oder anlegt, schneller oder langsamer um ihre Drehachse dreht.

Da die Physik schließlich zeitlich symmetrisch ist, d. h. heute und morgen gleich ist, bleibt die Energie nach dem Noether-Theorem erhalten. Man erkennt die Tragweite von Noethers Ergebnis: Die berühmte Aussage über die Erhaltung der Energie in einem isolierten System, nämlich dass „nichts entsteht und nichts vergeht, sondern alles sich umwandelt“, kann letztlich als Folge der Zeitinvarianz der physikalischen Gesetze angesehen werden.

Die grundlegende Rolle von Symmetrien in der Physik

Wir haben hier nur die grundlegendsten Beispiele für Symmetrien und Erhaltungssätze in der Natur angesprochen. Es wäre jedoch nur eine leichte Übertreibung zu sagen, dass die Hochenergiephysik zur eigentlichen Untersuchung der Symmetrien der Natur geworden ist. Es gibt noch viele weitere Symmetrien, die weniger intuitiv sind und eine entscheidende Rolle in der modernen Physik spielen. Wir werden hier einige davon aufzählen, ohne Anspruch auf Vollständigkeit oder eine tiefgehende Erklärung zu erheben.

Eichsymmetrien beispielsweise bilden den Kern einiger der erfolgreichsten Theorien, die jemals entwickelt wurden, vom Elektromagnetismus bis zum Standardmodell der Teilchenphysik. Bei Letzterem ist die Rolle der Symmetrien sogar noch bemerkenswerter, da sie den Physiker:innen praktisch sagten, wo (zum Beispiel in welchem Energiebereich) sie nach neuen Teilchen suchen mussten, die zu diesem Zeitpunkt noch unentdeckt waren. Und diese Teilchen wurden genau dort entdeckt, wo die Symmetrien hingedeutet hatten!

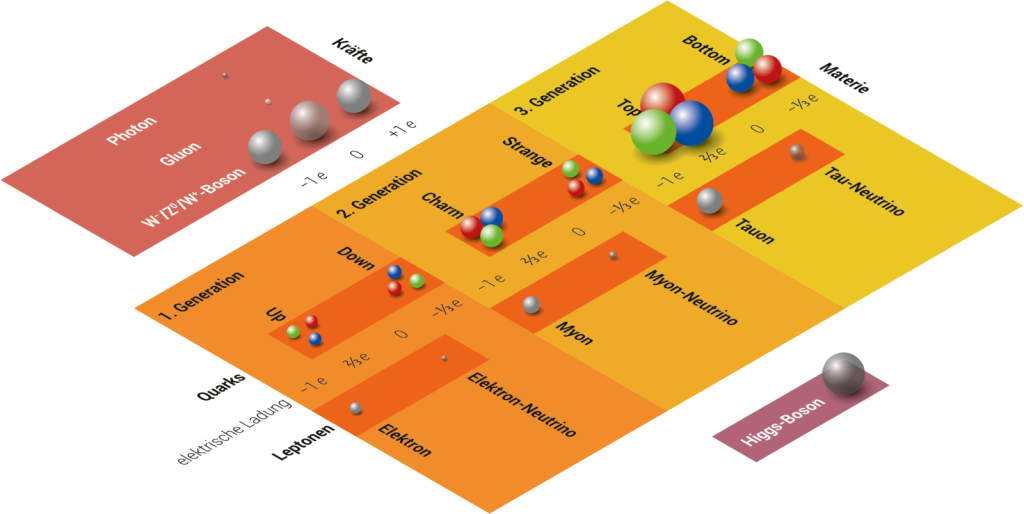
Inspiriert von diesen beeindruckenden Erfolgen stellten Forschende weitere Symmetrien theoretisch auf, deren Existenz noch zu beweisen ist, um ihre möglichen Auswirkungen auf bestehende Modelle zu untersuchen. Die Supersymmetrie beispielsweise sollte zwei verschiedene Klassen von Elementarteilchen miteinander in Verbindung bringen, die als Bosonen und Fermionen bekannt sind. Die Lichtteilchen (Photonen) gehören beispielsweise zur ersten Klasse, während die zweite Klasse die Materie umfasst, die uns umgibt und aus der wir bestehen, wie zum Beispiel Elektronen und Protonen. Teilchen, die zu diesen beiden Kategorien gehören, verhalten sich sehr unterschiedlich (zum Beispiel können Bosonen in großer Zahl „zusammengedrängt” werden, im Gegensatz zu Fermionen, die dies aufgrund des Pauli-Prinzips nicht können); die Supersymmetrie verbindet diese beiden Familien und sagt für jedes Teilchen der einen Art die Existenz eines zusätzlichen, entsprechenden „Partners” der anderen Art voraus (der allerdings noch nicht beobachtet wurde).

Zwei prominente Kandidatentheorien zur Vereinbarkeit von allgemeiner Relativitätstheorie und Quantenmechanik, nämlich die Stringtheorie und die Supergravitation, betrachten die Supersymmetrie als unverzichtbaren Bestandteil ihres Formalismus.

Und was ist mit dem Noether-Theorem? Alle oben genannten Symmetrien bilden keine Ausnahme und führen gemäß dem Theorem ihre eigenen Erhaltungsgrößen mit sich, was ein gutes Beispiel dafür ist, wie allgemein und allgegenwärtig Letzteres in der Physik ist. Diese Größen sind aus der Perspektive eines Laien weniger intuitiv zu verstehen, aber dennoch sehr nützlich bei der Durchführung von Berechnungen. Die mit der Supersymmetrie verbundene Erhaltungsgröße ist beispielsweise die sogenannte Superladung, die genau das Phänomen ist, das Bosonen in Fermionen umwandelt und umgekehrt.

Weniger konventionelle Symmetrien, die als Dualitäten bezeichnet werden, halten sich hingegen nicht an den Satz und tragen keine zugehörigen Erhaltungsgrößen: Sie sind keine Symmetrien im Lagrange-Formalismus, lassen aber dennoch die Dynamik des Systems unberührt. Im Zusammenhang mit der Stringtheorie waren die sogenannten U-Dualitäten von grundlegender Bedeutung, um zuvor als sehr unterschiedlich angesehene Modelle zu einer einzigen, allgemeineren und dennoch mysteriösen Theorie zu verbinden, die über die Strings selbst hinausgeht und als M-Theorie bezeichnet wird.

Eine weitere Art von Dualität ist die vermutete Verbindung zwischen einer Gravitationstheorie und einer Quantenfeldtheorie ohne Gravitation, bekannt als holografische Dualität zwischen Eichtheorie und Gravitation: Dies ist ein aktuelles Forschungsthema. Nach dieser Hypothese könnte unser Universum gleichermaßen gut durch eine Theorie der Quantengravitation oder rein durch eine zugehörige, gravitationsfreie Quantenfeldtheorie beschrieben werden.

Trotz der Abwesenheit von Gravitation muss diese Quantentheorie in einer Raumzeitdimension weniger existieren, als wir beobachten. In diesem Zusammenhang werden Symmetrien wieder grundlegend, da sie Schlüsselaspekte darstellen, die auf beiden Seiten der vermuteten Entsprechung verglichen werden müssen, um deren Gültigkeit zu überprüfen.

Wie wir gesehen haben, spielen Symmetrien und erhaltene Größen eine herausragende Rolle bei der Entwicklung physikalischer Theorien. Wurde Symmetrie in früheren Zeiten nur als eine nette Charakteristik eines physikalischen Systems angesehen, so hat sich die Situation in der modernen Physik völlig geändert, wo sie als grundlegendes Merkmal bei der Erstellung realistischer Modelle zur Beschreibung des Verhaltens unseres Universums übernommen wurde. Mit der Zeit wurde klar, dass Symmetrien in der Physik von wesentlicher Bedeutung sind und eine tiefe Bedeutung haben, so dass wir heute hoffen, dass sie ein vielversprechendes Leitprinzip für eine Theorie liefern könnten, die alle bekannten fundamentalen Wechselwirkungen vereint.

Weitere Informationen