Der mathematische Kosmos
Warum die Fragen nach Entstehung und Entwicklung der Welt als Ganzes eine Sache nicht nur der Physiker und Astronomen, sondern auch der Mathematiker ist.
Ein Artikel von Alan Rendall
Kosmologie, die Erforschung des Universums als Ganzes, ist nicht nur eine Angelegenheit der Astronomen und Astrophysiker, sondern auch der Mathematiker. Die Modelle der Kosmologen sind mathematischer Natur, und wer das Universum verstehen will, sollte sich nicht nur gute astronomische Beobachtungsdaten verschaffen – er sollte auch möglichst viel über die Eigenschaften der Gleichungen wissen, die den Kosmos beherrschen.
Anfangswerte und Evolution
Die physikalische Theorie, die unser Universum beschreibt und insbesondere, welche Rolle die Gravitation darin spielt, ist die Allgemeine Relativitätstheorie. Hinzu kommen Modelle für die Eigenschaften von Materie, etwa Gas oder elektromagnetischer Strahlung. Zusammengenommen ergeben sich Naturgesetze, die bestimmen, welche Eigenschaften der Kosmos haben kann und welche nicht, Gleichungen, denen jedes Universum gehorchen muss. Ein Universum, dass diesen Anforderungen genügt, ist in der Sprache der Mathematiker eine Lösung dieser Gleichungen, genau so wie x=-2 und x=4 Lösungen der quadratischen Gleichung x2 – 2·x-8=0 sind. In der Allgemeinen Relativitätstheorie wird das Gravitationsfeld durch die Einstein-Gleichungen beschrieben; nimmt man die physikalischen Gesetze hinzu, die die Eigenschaften der Materie bestimmen, erhält man ein Gleichungssystem, das man Einstein-Materie-Gleichungen nennen kann. Gemeinsam bestimmen diese Gleichungen, wie sich das Universum mit der Zeit weiterentwickelt; etwas abstrakter, aber genauer: sie bestimmen die Änderungsraten bestimmter physikalischer Größen in Abhängigkeit von den Werten, die diese Größen jetzt, in diesem Moment besitzen. Sobald die Werte der betreffenden Größen zu einem bestimmten Zeitpunkt festgelegt sind („Anfangswerte“) erlauben es die Gleichungen, die Werte zu jedem beliebigen späteren Zeitpunkt zu bestimmen. Diese Art, eine Lösung der Einstein-Gleichungen zu bestimmen, über ein so genanntes Anfangswertproblem, erlaubt es, die verschiedenen Lösungen zu klassifizieren und so eine Art Katalog der möglichen Lösungen der Einstein-Materie-Gleichungen aufzustellen. Wer konkrete kosmologische Modelle konstruieren möchte, um sie mit astronomischen Beobachtungsdaten zu vergleichen, kann sich aus diesem Katalog bedienen. Die Mathematik liefert die Bausteine, aus denen die Astrophysiker Universumsmodelle konstruieren.
Auf diese Weise wirklich alle Lösungen der Gleichungen zu bestimmen und alle Gleichungseigenschaften zu verstehen, ist freilich ein sehr vertracktes mathematisches Problem, und keines, das sich mit unserem heutigen Wissen lösen ließe. Fortschritte lassen sich trotzdem erzielen, dann nämlich, wenn man Modelle untersucht, in denen das Universum und die darin enthaltene Materie besonders einfache Eigenschaften haben und auch die Anfangswerte sehr einfach gewählt sind.
Homogene Universen
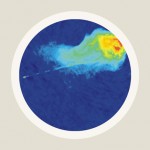
Eine grundlegende Vereinfachung legen bereits die astronomischen Beobachtungen nahe: unser Universum ist auf großen Skalen näherungsweise homogen (es sieht an jedem Ort gleich aus). Als Beispiel zeigt die folgende Abbildung einige Daten des 2dF Galaxy Redshift Survey. Am unteren Ende des Keils befindet sich der Beobachter. Die Keilform deutet an, dass nur eine begrenzte Himmelsregion durchforstet wurde. Jeder weisse Punkt steht für eine Galaxie, einige näher am unteren Ende des Keils (und damit näher an der Erde), andere weiter entfernt. Die weiteste dargestellte Entfernung, der obere Begrenzungsbogen, entspricht einer Entfernung von rund 2 Milliarden Lichtjahren von der Erde:

Zwar zeigt die Verteilung der Galaxien eine deutliche schwammartige Struktur, mit dichteren und ausgedünnten Regionen. Wenn man den Raum dagegen in Würfel mit einigen hundert Millionen Lichtjahren aufteilt, ist die mittlere Dichte jedes dieser Würfel die gleiche – auf großen Skalen ist das Universum homogen.
Man kann daher ein nützliches Modelluniversum konstruieren, einfach und doch nicht zu weit von der Realität entfernt, indem man annimmt, das Universum sei exakt homogen. Solche Modelle sind mathematisch verhältnismäßig leicht zu behandeln, und die meisten Vorhersagen der modernen Kosmologie basieren auf solchen vereinfachten Modelluniversen. Allerdings darf man dabei nicht vergessen, dass es sich um eine Vereinfachung handelt, und das wirft eine Frage auf, die Mathematikern wohlbekannt ist und auf die „Stabilität“ von Lösungen zielt: Ist eine bestimmte Lösung ein untypischer Spezialfall oder kann sie stellvertretend für die allgemeinere Situation stehen, die untersucht wird? Etwas anders ausgedrückt: Wenn man ein wenig von der Idealisierung abweicht, etwa anstatt eines homogenen Modells eines mit Regionen leicht größerer und geringerer Dichte betrachtet, führt das zu drastischen Veränderungen im Verhalten des Modells? Oder ist die Zeitentwicklung nach wie vor im großen und ganzen dieselbe wie im vereinfachten Modelluniversum – und das vereinfachte Modell damit ein guter Anhaltspunkt dafür, wie die Zeitentwicklung komplizierterer Universen verläuft? Um Antworten auf solche Fragen zu bekommen, kann man insbesondere Anfangswerte untersuchen, die sich ein winziges bisschen von denen eines sehr einfachen Universums mit hoher Symmetrie unterscheiden.
De Sitters Universum
Ein konkretes Beispiel für Stabilitätsüberlegungen ist der Fall beschleunigt expandierender Universen – eines Kosmos mit einer positiven kosmologischen Konstanten oder, allgemeiner, ein Weltall, das dunkle Energie enthält. Mathematiker kennen bereits seit 1917 eine Lösung der Einstein-Gleichungen, die ein Universum ganz ohne Materie aber mit positiver kosmologischer Konstanten beschreibt. Diese de-Sitter-Lösung ist ein sehr einfaches Modell für ein Universum mit beschleunigter Expansion. Fügt man ihr Materie hinzu, die ganz gleichmäßig im Weltall verteilt ist, dann ändert sich nichts an den grundlegenden Eigenschaften dieser Lösung – zumindest gegenüber dieser Veränderung ist die de-Sitter-Lösung stabil. Die materiefreie Lösung erweist sich als nützlicher Anhaltspunkt für die Eigenschaften eines herkömmlichen, mit Materie gefüllten Kosmos.
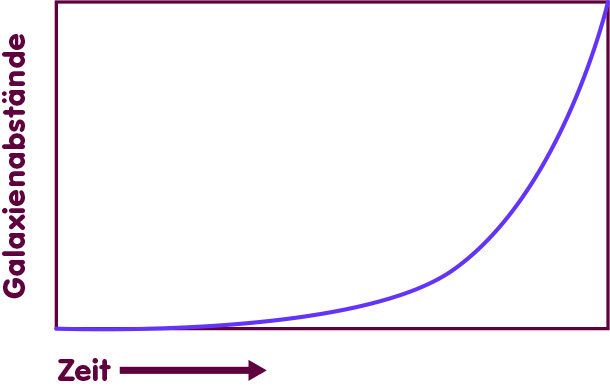
In Lösungen dieser Art nimmt der Abstand zwischen frei fallenden Galaxien mit der Zeit exponentiell zu, wie in der folgenden Grafik skizziert:
In einer Arbeit aus dem Jahr 1986 konnte erstmals gezeigt werden, dass die de-Sitter-Lösung auch in anderer Hinsicht stabil ist – zumindest, solange keine Materie ins Spiel kommt: Man kann die Homogenität des betreffenden Modell-Universums stören, indem man in das modellierte Weltall schwache Gravitationswellen einbringt, entsprechend winzigen Verzerrungen, durch die das Weltall dann nicht mehr perfekt homogen ist. Doch selbst mit solchen Störungen, solchen leichten Abweichungen von der Homogenität kommt immer noch ein exponentiell expandierendes Universum heraus. Je mehr Zeit in diesem Universum vergeht, umso ähnlicher wird seine zeitliche Entwicklung der eines perfekt homogenen de-Sitter-Weltalls.
Es ist den Mathematikern bislang noch nicht gelungen, einen entsprechenden Beweis für ein beschleunigtes Universum zu führen, das Materie enthält. Zwar gibt es Plausibilitätsargumente dafür, dass die Anwesenheit von Materie die Situation nicht grundlegend ändert, eine Aussage, die auch als „kosmisches keine-Haare-Theorem“ bekannt ist. Das Interesse an solch einem Beweis liegt auf der Hand – unser eigenes Universum ist nach den Beobachtungen der astronomen gerade solch ein beschleunigt expandierendes Universum. Ein Stabilitätsbeweis würde die Praxis der Kosmolgen, von vereinfacht homogenen Weltmodellen auf das wirkliche Universum zu schließen, mathematisch rechtfertigen. Er würde auch bedeuten, dass ein leicht inhomogenes Universum mit der Zeit einem perfekt homogenen Universum immer ähnlicher wird, genau so wie im materiefreien Fall. Damit ließe sich verstehen, wie sich ein homogenes Universum wie das unsrige im Laufe der kosmischen Expansion ganz von selbst ergeben haben könnte, ohne, dass man sehr spezielle Anfangsbedingungen postulieren müsste. Doch leider lässt sich das Beweisverfahren, das im materiefreien Fall zum Erfolg führte, nicht auf direktem Wege an die neue Situation anpassen – ein Umstand, der die Mathematiker vor eine gehörige Herausforderung stellt. Bislang konnten sie den Beweis nur für ausgewählte, sehr symmetrische Spezialfälle finden.
Parallel zu den hier beschriebenen Forschungen werden Modelle untersucht, die außer der herkömmlichen Materie der Galaxien noch exotischere Materieformen enthalten – etwa die so genannte Quintessenz, ein Versuch, die beschleunigte Expansion nicht auf Einsteins kosmologische Konstante zurückzuführen, sondern auf Materie mit einer Art negativem Druck. Das ist sinnvoll, da die Kosmologen derzeit nicht wissen, was wirklich hinter der beschleunigten Expansion unseres Weltalls steckt – es ist daher ratsam, sich nicht zu früh festzulegen und eine recht allgemein gefasste Klasse von Modellen mit beschleunigter Expansion zu untersuchen.
Weitere Informationen
Die relativistischen Grundkonzepte, die diesem Vertiefungsthema zugrundeliegen, werden in Einstein für Einsteiger erklärt, insbesondere im Abschnitt Kosmologie.
Verwandte Vertiefungsthemen auf einstein-online finden sich in der Kategorie Kosmologie.
Informationen über die Hintergründe der obigen Abbildung finden sich auf den
Kolophon
ist Professor für Mathematik an der Johannes-Gutenberg-Universität Mainz.
Zitierung
Zu zitieren als:
Alan Rendall, “Der mathematische Kosmos” in: Einstein Online Band 04 (2010), 01-1133