General relativity
Foundations of Einstein’s theory of gravity: Einstein and soap bubbles, what is a source of gravity, the equivalence principle and free fall
This page features an overview of all our Spotlights on Relativity dealing with the basic features of general relativity. The spotlight texts under the heading Fundamentals deal with the equivalence principle, the equal rights of all observers and the question which properties of a body determine its gravitational influence. The section General relativity and light examines gravity’s influence on the propagation and properties of light, while Singularities takes a look at some of the theory’s more disturbing predictions for the interior of black holes and the beginning of our universe. The mathematics of general relativity is all about the more mathematical aspects of Einstein’s theories – from the surprising connection to the theory of soap bubbles to the question of how much variety Einstein’s equations admit. The focus of the section Numerical relativity are computer simulations of complex relativistic phenomena, such as merging black holes. Under Miscellaneous, there is a text on the relativistic Nobel prizes.
Many more Spotlights concerned with specific consequences and applications of general relativity can be found on the overview pages Gravitational Waves, Black Holes & Co., Cosmology and Relativity and the Quantum.
Useful background information can be found in our introduction Elementary Einstein, especially in the chapter General Relativity.
The basics of general relativity
The elevator, the rocket, and gravity: the equivalence principle
Information about the principle that Einstein took as a starting point for developing his general theory of relativity
Gravity: from weightlessness to curvature
So what is gravity in Einstein’s theory? The answer: in part, an illusion; in part, an aspect of geometry.
…that all coordinate systems are created equal
Why, in general relativity, all observers are on an equal footing – and why, nevertheless, you can say that the earth orbits the sun, but not the other way around
Inertial and Gravitational Mass
About the different roles played by mass, and the weak equivalence principle
A subtle change in direction: Geodetic precession
In Einstein’s theory, gravity is related to spacetime curvature. This text explores what curvature is – and how the way it influences geometry can be measured directly, with the help of gyroscopes.
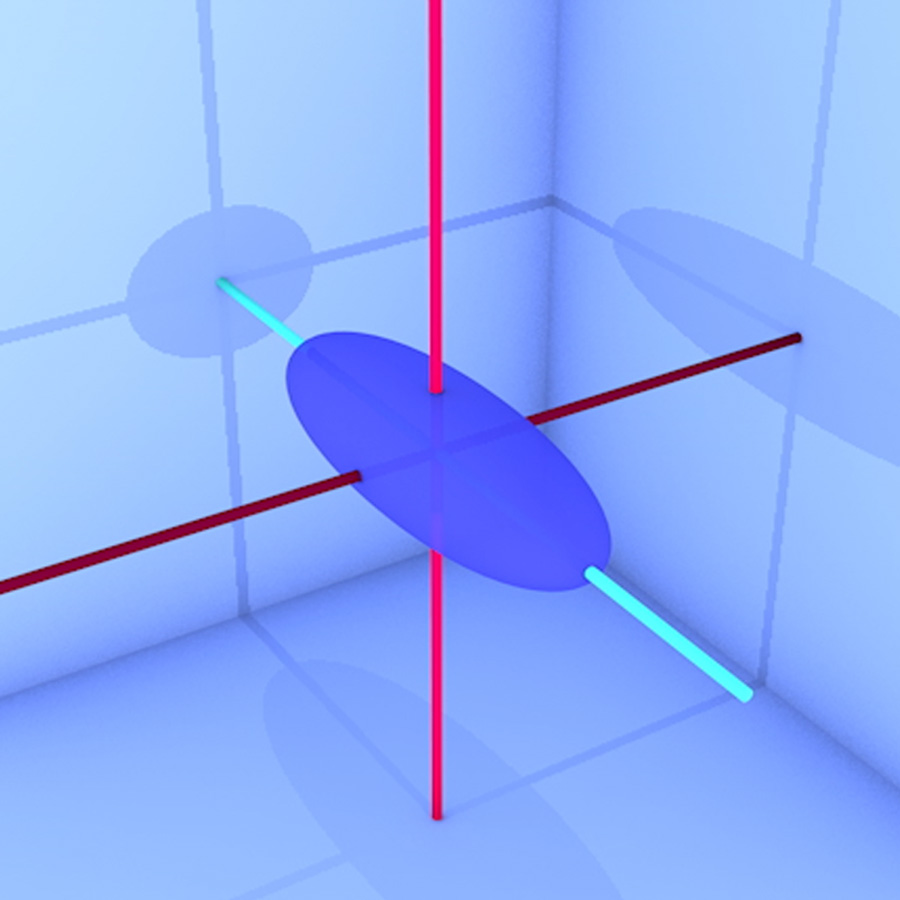
Mass and other sources of gravity
Mass and more
An account of which physical properties act as sources of gravity – includes consequences for collapsing stars and for cosmology
The gravity of gravity
An important property of gravity in Einstein’s theory is that it can create more gravity. The result is “non-linearity” – the gravitational influence of two bodies isn’t just the sum of their separate influences!
Light in general relativity
Measuring light deflection with radio telescopes
Very long baseline interferometry (VLBI) can be used to measure deflection of light by the sun with very high accuracy, which allows the testing of a prediction of general relativity.
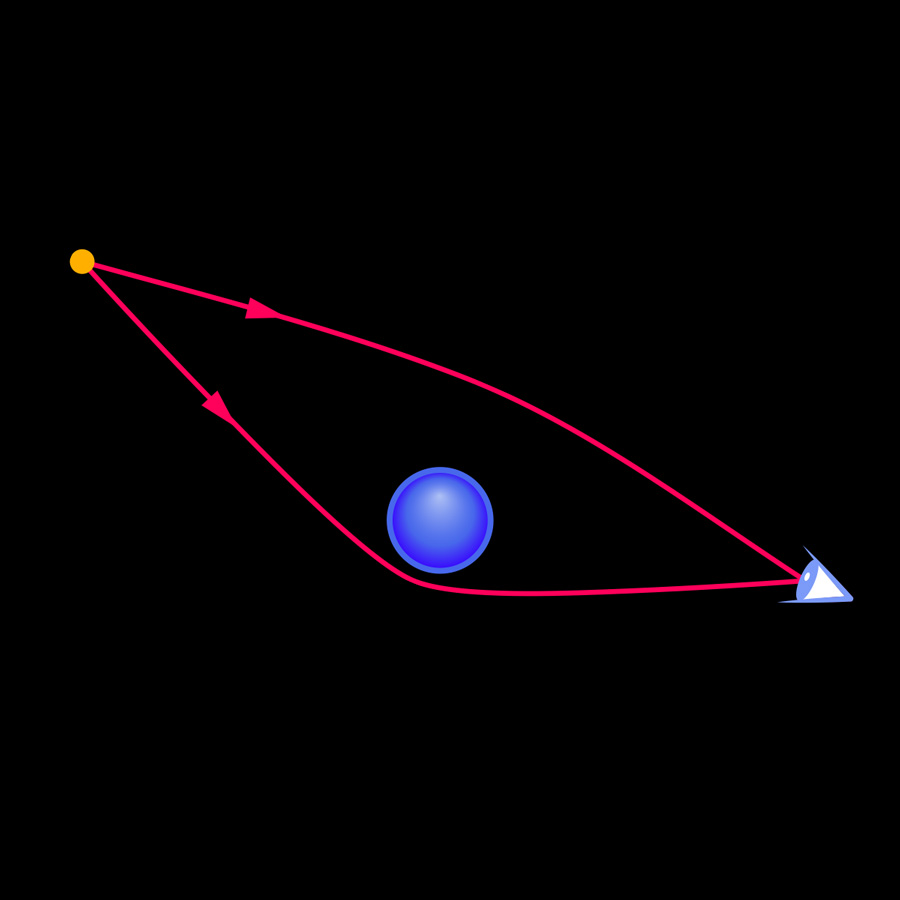
Gravitational deflection of light
On one of the fundamental consequences of general relativity: the deflection of light by gravity
The equivalence principle and the deflection of light
The connection between one of the fundamental principles of general relativity and the gravitational deflection of light
A brief history of gravitational lensing
Historical sketch of the derivation of general relativity’s prediction of gravitational lenses and subsequent astronomical observations
Gravitational redshift and White Dwarf stars
One of the fundamental effects predicted by general relativity, and some of its astronomical applications
Singularities
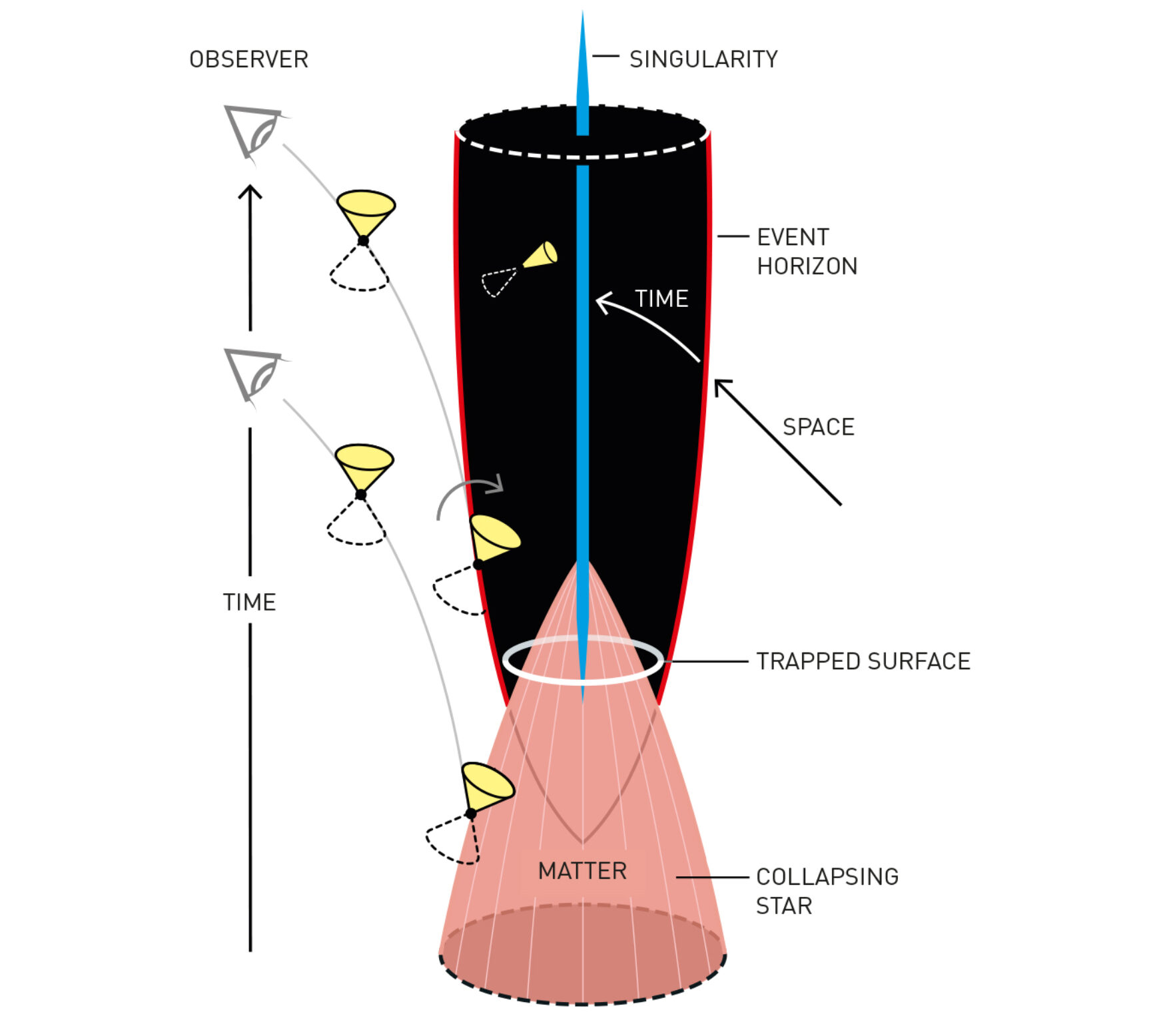
The Singularity Theorem (Nobel Prize in Physics 2020)
In 2020, Roger Penrose was awarded half of the Nobel prize in physics for proving that black hole formation is a robust prediction of Einstein’s general theory of relativity.
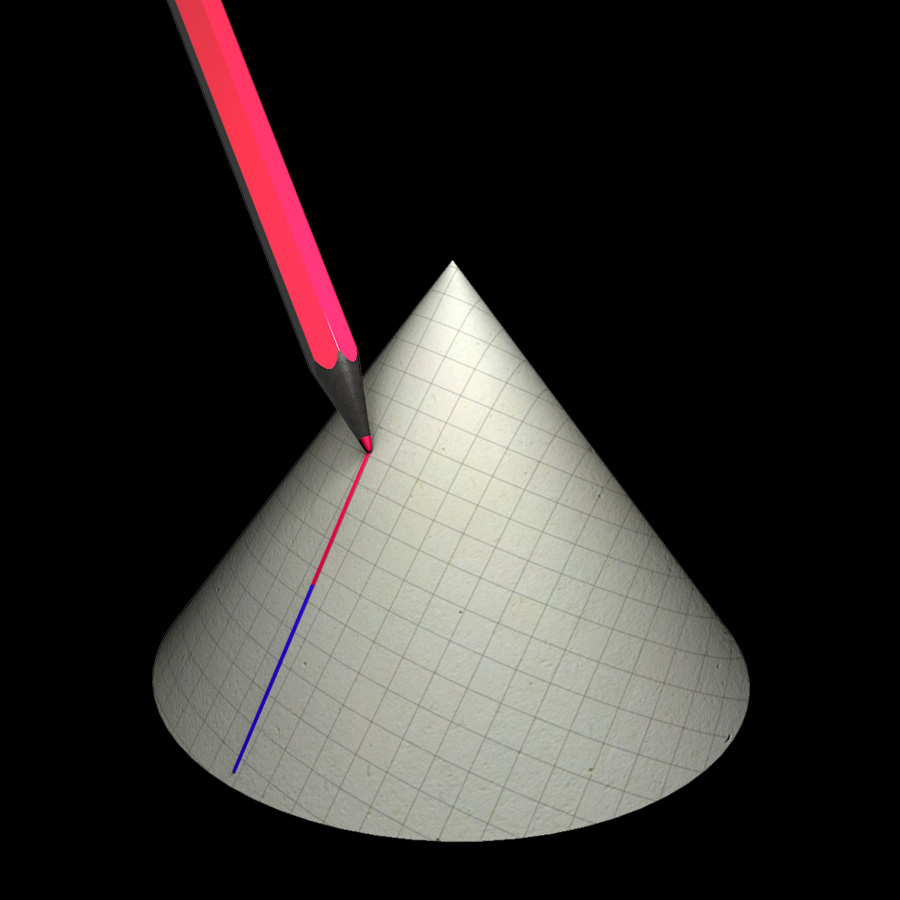
Spacetime singularities
Information about the most disturbing feature of Einstein’s theory – ragged edges of spacetime known as singularities.
Of singularities and breadmaking
About some characteristic properties of spacetime near singularities – and the violent deformations they cause for any object unlucky enough to approach a singularity
Numerical relativity
Multi-messenger astrophysics and numerical relativity
During neutron star mergers, both gravitational wave and electromagnetic signals are emitted. This could help solve long-standing issues in basic physics research with multi-messenger astrophysics.
The realm of relativistic hydrodynamics
Modeling relativistic fluids and the phenomena associated with them – from supernovae and jets to merging neutron stars
From Newton to Einstein - and beyond
Varying Newton’s constant: A personal history of scalar-tensor theories
Information about a modification of Einstein’s theory of general relativity in which the gravitational constant is not a constant.
The mathematics behind general relativity
The Singularity Theorem (Nobel Prize in Physics 2020)
In 2020, Roger Penrose was awarded half of the Nobel prize in physics for proving that black hole formation is a robust prediction of Einstein’s general theory of relativity.
From soap bubbles to Einstein
Most readers will know them from childhood: soap bubbles
The many ways of building an empty, unchanging universe
More information on one particular answer to the question of how much variety is permitted in general relativity – how many ways are there of constructing a universe that is completely empty of all matter?
Miscellaneous
Einstein’s Nobel heritage
An overview of Nobel prizes connected with relativistic physics