Von Gravitationswellen und kugelförmigen Hühnern
Informationen über eine Klasse von einfachen Modelluniversen – jedes ein expandierender Kosmos, der mit Gravitationswellen gefüllt ist
Ein Artikel von Robert H. Gowdy
Aussagen über kugelförmige Hühner sind die Pointe einer Reihe von Physikwitzen. Sie beziehen ihre Komik aus der Art und Weise, wie Physikerinnen und Physiker denken. Doch diese Denkweise hat durchaus ihre Berechtigung. Oft führt eine extreme Vereinfachung zu einer Situation, die mit Bleistift und Papier vollständig verstanden werden kann und Trends offenbart, die zwischen den Details einer vollständig realistischen Berechnung vielleicht untergegangen wären. Eine reale Situation, an deren Verständnis wir interessiert sind, ist das frühe Universum, und eine Vereinfachung, die uns hilft, bestimmte Aspekte davon zu verstehen, sind die sogenannten Gowdy-Raumzeiten.
Gravitationswellen im frühen Universum
Es ist die Zeit kurz nach der ersten Urknallsingularität. Gravitationswellen sind überall, mit allen möglichen Wellenlängen, in alle Richtungen unterwegs. Die extreme Vereinfachung dieser Situation ist, Folgendes anzunehmen:
1. Es ist keine Materie vorhanden.
2. Alle Gravitationswellenfronten sind parallel zueinander und verdrehen sich nicht.
3. Das gleiche Wellenmuster wiederholt sich immer wieder im Raum.
Die erste Annahme ist leicht zu verstehen. Die zweite kann wie folgt verstanden werden: Wenn sich Gravitationswellen durch den Raum bewegen, werden zu jedem Zeitpunkt einige Regionen des Raums maximal verzerrt (siehe den Vertiefungstext Die Wellennatur der Gravitationswellen). Für die einfachen Wellen, die wir hier betrachten, sind diese Regionen mit maximaler Verzerrung Ebenen. Wenn sich das Wellenmuster wiederholt, werden diese Regionen etwa so übereinander gestapelt:

Die zusätzliche Annahme, dass diese Ebenen sich nicht verdrehen, bedeutet, dass sie nicht verdreht sind wie ein Kartenstapel, bei dem jede Karte in einem Winkel zur darunter liegenden gedreht ist:

Diese Zusatzannahme heißt Zwei-Flächen-Orthogonalität.
Die Annahme, dass sich die Wellen wiederholen, könnte bedeuten, dass sich der Raum unendlich weit ausdehnt, das Wellenmuster sich aber wie die Fliesen auf einem Fußboden wiederholt – wie im folgenden Bild, das Kacheln mit einem einfachen Muster zeigt, das nichts mit Gravitationswellen zu tun hat:

Natürlich ist der Fußboden eine zweidimensionale Fläche, während die sich wiederholenden Wellenmuster den dreidimensionalen Raum ausfüllen.
Auf solch einer gekachelten Oberfläche (oder in solch einem gekachelten Raum) läuft ein Objekt, das die Grenze einer bestimmten Kachel überschreitet, einfach auf der nächsten identischen Kachel weiter, wie es bei dem sich bewegenden roten Quadrat in der folgenden Animation der Fall ist. Auf seiner Rundreise besucht das Quadrat vier verschiedene Kacheln:

Diese perfekte Regelmäßigkeit könnte aber auch so verstanden werden, dass der Raum selbst aufgerollt ist, so dass jedes Objekt, das durch eine „Kachelgrenze“ hinausgeht, durch eine andere Grenze wieder in dieselbe Kachel zurückkommt, wie in dieser Animation gezeigt:

Wenn wir bereit sind, die Kachel zu verzerren, ist es möglich, direkt zu zeigen, wie dieser neue Ein-Kachel-Raum aussieht. Hier ist eine einfache Kachel ohne Muster:

Wir müssen jeweils die beiden türkisblauen und die beiden roten Kanten zur Deckung bringen – etwa, indem wir die Kanten zusammenkleben. Klebt man zwei gegenüberliegende Kanten zusammen, so entsteht ein Rohr. Klebt man dann noch die Kanten des Rohres zusammen, ergibt sich ein Donut oder Torus:

Für dreidimensionale Kacheln, also gewissermaßen massive Würfel, gibt es eine analoge Konstruktion. Das Ergebnis ist ein Objekt, das „dreidimensionaler Torus“ genannt wird. Auf einem solchen dreidimensionalen Torus würden sich die Gravitationswellen einfach gegenseitig umherjagen, ähnlich wie hier für geschlossene Linien gezeigt, die Wellenfronten auf der Oberfläche eines gewöhnlichen zweidimensionalen Torus darstellen:
Der Übersichtlichkeit halber sind hier nur Wellen dargestellt, die sich in einer Richtung um den Torus bewegen. Eigentlich sagen uns die Einsteinschen Gleichungen, dass es in diesen geschlossenen Universen immer auch Wellen geben muss, die sich in die entgegengesetzte Richtung bewegen.
Angesichts der beiden unterschiedlichen Interpretationen der perfekten Regelmäßigkeit können wir, wenn unsere dritte Annahme gilt, zwei sehr unterschiedliche Situationen modellieren: ein unendliches Universum mit Gravitationsstrahlung, die auf großen Skalen gleichmäßig verteilt ist (alle Kacheln sind gleich) und ein geschlossenes Universum (nur eine Kachel). Unser vereinfachtes Modell wird üblicherweise als Gowdy-T3-Raumzeit bezeichnet, wobei T3 für das geschlossene „dreidimensionale Torus“-Universum mit nur einer Kachel steht.
Wendet man die Einsteinschen Feldgleichungen auf diese Situation an, so zeigt sich sofort, dass die Entwicklung dieser Modelluniversen analog zu den häufigeren Urknallmodellen verläuft: Sie haben einen abrupten und unbestimmten Anfang – eine Anfangssingularität –, und danach dehnt sich das gesamte Universum immer weiter aus.
An dieser Stelle können wir eine weitere vereinfachende Annahme machen, nämlich
4. Nur eine der beiden möglichen Gravitationswellenpolarisationen ist vorhanden.
Dies läuft darauf hinaus, dass unsere Gravitationswellen besonders einfach sind – die Richtungen der maximalen Raumverzerrung sind für alle gleich. Mit dieser zusätzlichen Simplifikation werden die Einsteinschen Gleichungen so einfach, dass sie tatsächlich mit Bleistift und Papier gelöst werden können: Mit einfachen mathematischen Funktionen wie Sinus oder Kosinus ist es möglich, eine Beschreibung für alle möglichen Raumzeiten dieses Typs aufzuschreiben. Modelluniversen, die sich auf diese Weise einfach aufschreiben lassen, nennt man exakte Lösungen der Einsteinschen Gleichungen. Die hier diskutierten speziellen Raumzeiten werden üblicherweise „polarisierte Gowdy-T3-Raumzeiten“ genannt.
Im Prinzip wissen wir alles, was es über polarisierte Gowdy-T3-Raumzeiten zu wissen gibt. Darum können wir sie verwenden, um unsere Vorstellung von allgemeineren Situationen auf die Probe zu stellen. Zum Beispiel könnte man vermuten, dass intensive Gravitationswellen zur Bildung von Raumzeitkanten – Singularitäten – führen können, die nicht durch einen Ereignishorizont abgeschirmt sind. Solch nackte Singularitäten soll es laut der Hypothese der kosmischen Zensur nicht geben. Tatsächlich bilden sie sich auch in den polarisierten Gowdy-T3-Raumzeiten nicht – Vertreter dieser Hypothese haben also hiervon keine Gegenbeispiele zu befürchten.
Eine andere Hypothese, die BKL-Vermutung, betrifft die Eigenschaften der Raumzeit in der Nähe der Anfangssingularität. Sie besagt, dass man beim Betrachten einer kleinen Raumregion nicht zwischen dieser und fast allen anderen Raumzeiten mit einer Anfangssingularität unterscheiden kann. In der Nähe der Singularität zeigen alle diese Universen das gleiche Verhalten (siehe das Vertiefungsthema Singularitäten als Raumzeit-Knetmaschinen). Diese Vermutung hält auch in den polarisierten Gowdy-T3-Raumzeiten stand.
Testen numerischer Simulationen von Gravitationswellenquellen
Eine weitere reale Situation, an deren Verständnis wir interessiert sind, ist die Art von Gravitationswellenzug, der entsteht, wenn zwei Neutronensterne oder zwei Schwarze Löcher spiralförmig ineinander übergehen und miteinander verschmelzen. In dieser Situation gibt es keine Symmetrie und keine Möglichkeit, ein „kugelförmiges Huhn“ zu Rate zu ziehen, das uns viel über die Antwort verrät. Uns bleibt nur, die ganze Situation auf einem Computer zu simulieren.
Der Computer verwendet eine endliche Menge von Zahlen, um eine kontinuierliche Unendlichkeit von Punkten zu beschreiben. Da das ein riskantes und fehleranfälliges Verfahren ist, brauchen wir eine Möglichkeit, es zu überprüfen. Die Gowdy-T3-Raumzeiten sind nicht vergleichbar mit einem Paar sich umkreisender Neutronensterne oder Schwarzer Löcher, aber sie beschreiben eine komplexe Situation, die wir vollständig verstehen. Daher können sie zur Validierung von Computersimulationsverfahren dienen. Typischerweise arbeitet ein Simulationsprogramm mit einer Momentaufnahme der Geometrie von Raum und Zeit („Anfangsdaten“); dann berechnet es mithilfe der Einsteinschen Gleichungen, wie sich diese Situation mit der Zeit entwickelt. Für eine polarisierte Gowdy-T3-Raumzeit können wir explizit aufschreiben, wie sich jede Anfangssituation mit der Zeit entwickelt – wir kennen also die richtige Antwort. Wenn eine Computersimulation mit Anfangsdaten gestartet wird, die der Momentaufnahme einer polarisierten Gowdy-T3-Raumzeit entsprechen, und Ergebnisse liefert, die mit der bekannten Lösung übereinstimmen, dann besteht sie den Test. Das folgende Bild zeigt ein Beispiel:
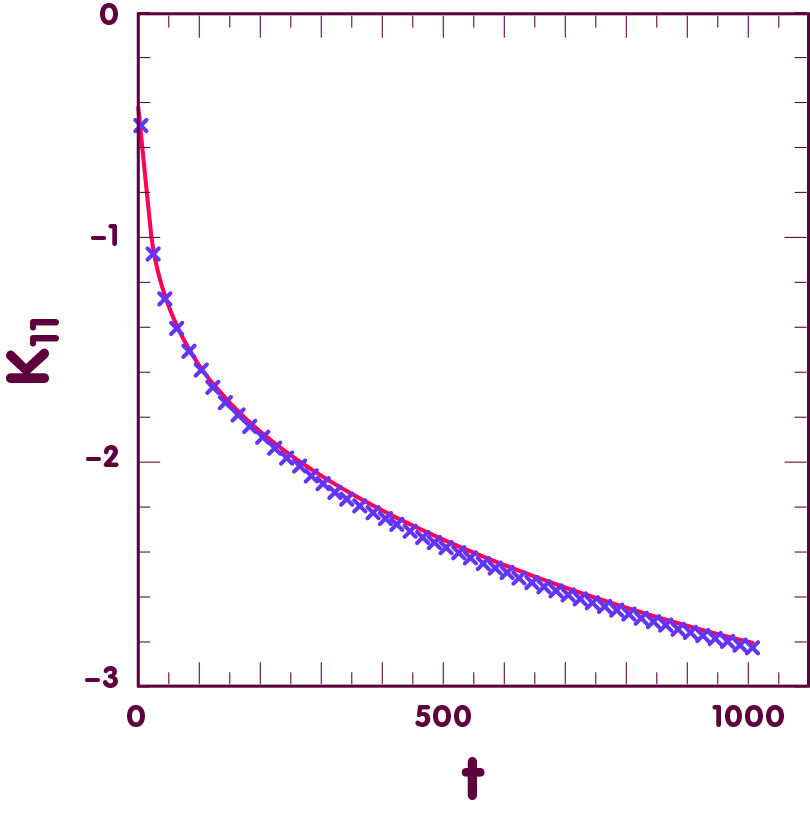
[Bilddaten von K. C. B. New et al., Phys.Rev. D58 (1998) 064022]
Fokussierte Gravitationswellen
Unter geeigneten Bedingungen können Wellen divergieren oder konvergieren, also auf einen Fokuspunkt zulaufen. Bei Lichtwellen erreicht man diesen Effekt mithilfe einer Linse. Bei Wasserwellen kann ein in einen Teich geworfener Stein einen „inversen Brennpunkt“ erzeugen, von dem aus sich die Wellen nach außen ausbreiten, hier von oben gesehen:
Die Wellen in einer Gowdy-T3-Raumzeit laufen niemals in einen Brennpunkt. Wir könnten aber vermuten, dass die Einführung fokussierter Gravitationswellen zu neuen Phänomenen führen könnte. Ersetzen wir nämlich die Annahme periodischer Wellen durch die Annahme, dass die Wellen an zwei Stellen zu einem (zylindrischen) Brennpunkt laufen, so erhalten wir eine weitere Familie einfacher Raumzeiten, deren Eigenschaften sich mit Bleistift und Papier ausarbeiten lassen. In diesen Raumzeiten ist der Raum endlich und auf sich selbst gekrümmt in einer von zwei verschiedenen Verallgemeinerungen der bekannten Geometrie einer Kugel. (Diese Lösungen, Gowdy S¹xS²- und Gowdy S³-Raumzeiten, sind wirklich „kugelförmige Hühner“.) Die folgende Animation zeigt einen zweidimensionalen Ausschnitt aus einer dieser Raumzeiten, einschließlich einiger der Gravitationswellenfronten. Man sieht, wie diese Wellen an einem Brennpunkt „emittiert“ werden und an der Kugel entlanglaufen, bevor sie an einem anderen Brennpunkt „absorbiert“ werden:

Dies ist wiederum ein vereinfachtes Bild; genau wie im Fall des Torus wird es auch in diesen Raumzeiten Wellen geben, die sich in die andere Richtung bewegen.
Das Vorhandensein von Stellen, an denen sich die Wellen zu einer Linie fokussieren, macht diese Lösungen etwas komplexer als die T3-Raumzeiten, so dass sie nicht so umfassend erforscht sind. Aber es scheint klar, dass sie zumindest keine nackten Singularitäten bilden, so dass die kosmische Zensurhypothese auch hier vor Gegenbeispielen sicher ist.
Die verbleibende Möglichkeit ist sowohl sehr alt als auch sehr neu. Ersetzt man die Annahme periodischer Wellen durch die Annahme, dass die Wellen zylindrisch – also auf eine Linie fokussiert – sind, so ergeben sich zwei Familien von exakt lösbaren Raumzeiten. Die eine ist die Einstein-Rosen-Zylinderwellenlösung, die 1937 veröffentlicht wurde und die Grundlage für frühe Argumente zu Gravitationswellen bildete. Sie kann wie in der folgenden Animation dargestellt werden, die eine kubische Raumregion mit expandierenden Zylinderwellenfronten zeigt:

Die andere Raumzeit entspricht Zylinderwellen in einem expandierenden Universum und wurde 2007 veröffentlicht. Beide Arten von Lösungen fungieren als einfache Modelle für Gravitationswellen, die sich von einer endlichen Quelle wie einem Paar sich umkreisender Schwarzer Löcher ausbreiten.
Wechselwirkende Gravitationswellen
Alle diese unterschiedlichen Annahmen – periodische Wellen, zwei-Fokus-Wellen und zylindrische ein-Fokus-Wellen – führen zu exakten, mit Bleistift und Papier auffindbaren Lösungen der Einsteinschen Feldgleichungen, sofern die Gravitationswelle nur eine Polarisation hat. Erlaubt man kompliziertere Fälle, indem man die andere Polarisation zulässt, so ergeben sich sogenannte „unpolarisierte Gowdy-Raumzeiten“. Im Gegensatz zum polarisierten Fall ist es unmöglich, eine vollständige Beschreibung dieser Raumzeiten aufzuschreiben. Und trotzdem sind sie vergleichsweise einfach, da sie die komplexen Einsteinschen Feldgleichungen auf viel einfachere Gleichungen für zwei miteinander wechselwirkende Wellen reduzieren. Diese Raumzeiten bieten eine Art „Spielmodell“ von Einsteins Gravitationstheorie, bei dem viele der Komplikationen beseitigt sind. Mit ihnen können wir unser Verständnis dessen, was Einsteins Theorie in realistischeren Situationen vorhersagt, auf Herz und Nieren prüfen. Es ist zum Beispiel recht einfach, Computerprogramme zu schreiben, die unpolarisierte Gowdy-Raumzeiten simulieren und die Art und Weise untersuchen, wie verschiedene Gravitationswellenpolarisationen miteinander interagieren. Ein faszinierendes Ergebnis ist, dass reguläre Wellen interagieren können, um so genannte „Spikes“ zu erzeugen.
Die folgende Animation basiert auf den Ergebnissen einer numerischen Simulation einer unpolarisierten Gowdy-Raumzeit. Sie zeigt, wie sich die Amplitude einer der beiden wechselwirkenden Gravitationswellen im gesamten Raum (genauer: in einer bestimmten Raumrichtung) ändert. In der Animation läuft die Zeit rückwärts – die Animation beginnt zu einem bestimmten Zeitpunkt und folgt dann der Entwicklung des sich ausdehnenden Gowdy-Universums rückwärts, immer näher zur Anfangssingularität:
[Animation: D. Garfinkle, Oakland University]
Alles in allem eröffnen Gowdy-Raumzeiten eine Vielzahl von Möglichkeiten, die Struktur von Einsteins Universum zu erforschen – ein Beleg dafür, dass auch kugelförmige Hühner nützliche Tiere sind.
Weitere Informationen
Die relativistischen Ideen hinter diesem Vertiefungsthema finden Sie in Einstein für Anfänger, insbesondere in den Kapiteln Allgemeine Relativitätstheorie und Gravitationswellen.
Verwandte Vertiefungsthemen zur Relativitätstheorie finden Sie in den Abschnitten Allgemeine Relativitätstheorie und Gravitationswellen.
Kolophon
ist Professor für Physik an der Virginia Commonwealth University. Sein Hauptforschungsinteresse gilt den geometrischen Eigenschaften von Raumzeiten, die aus Einsteins Gleichungen folgen.
Zitierung
Zu zitieren als:
Robert H. Gowdy, “Von Gravitationswellen und kugelförmigen Hühnern” in: Einstein Online Band 13 (2021), 1102










