Singularitäten als Raumzeit-Knetmaschinen
Über einige charakteristische Eigenschaften der Raumzeit in der Nähe einer Singularität – insbesondere die Verformungen, die jedes Objekt erfährt, welches der Singularität zu nahe kommt.
Ein Artikel von David Garfinkle
Der Gravitationskollaps massereicher Sterne kann dazu führen, dass ein Schwarzes Loch entsteht: eine Region der Raumzeit in der die Gravitation so stark ist, dass nichts, was einmal hineingelangt ist, jemals wieder entkommen kann – noch nicht einmal Licht. Daraus ergibt sich, dass wir niemals in das Innere eines Schwarzen Lochs werden hineinsehen können. Nichtsdestoweniger können wir aber fragen, was uns die Allgemeine Relativitätstheorie, die Grundlage für die mathematische Beschreibung Schwarzer Löcher, über die Innenregionen zu sagen hat. Ein wichtiger Aspekt der Antwort wird Sie vielleicht überraschen: Was mit einem Objekt geschieht, das in ein Schwarzes Loch gefallen ist, hat eine gewisse Ähnlichkeit mit der Art und Weise, wie ein Bäcker Teig knetet!
Das Ende des freien Falls
Aus der Allgemeinen Relativitätstheorie folgt, dass der Kollaps eines massereichen Sternes auch dann nicht aufhört, wenn sich ein Schwarzes Loch gebildet hat – auch im Inneren des Schwarzen Lochs fällt die Materie weiter nach innen. Nichts kann sich schneller bewegen als das Licht, und im Inneren eines Schwarzen Lochs wird selbst Licht durch den Einfluss der Gravitation immer weiter nach innen gezogen. In einem Schwarzen Loch könnte nur am gleichen Ort bleiben (oder sich gar nach außen bewegen und entkommen!), wer imstande wäre, sich schneller zu bewegen als das Licht.
Beim fortgesetzten Kollaps wächst die Dichte der fallenden Sternmaterie über alle Grenzen – oder erreicht zumindest die unvorstellbar großen Dichtewerte, bei denen Effekte der Quantengravitation wichtig werden sollten. Lässt man Quanteneffekte außer acht, so sollte die Dichte sogar unendlich groß werden. Dann ist die so genannte Singularität des Schwarzen Loches erreicht.
Erreicht ein Beobachter, der das Pech hatte, in das Schwarze Loch hinein zu fallen, die Singularität, dann hört er schlicht auf zu existieren. Tatsächlich ist der Umstand, dass die Existenz eines frei fallenden Beobachters dort ein jähes Ende findet, die übliche Definition einer Singularität (weitere Informationen bietet das Vertiefungsthema Raumzeitsingularitäten). Diese Definition wird in einer Reihe berühmter Theoreme verwendet, die Singularitätentheoreme heißen. Sie zeigen, dass Singularitäten dieser Art im Rahmen der Allgemeinen Relativitätstheorie in gewissen Situationen unausweichlich entstehen – etwa, wenn hinreichend massereiche Sterne kollabieren.
Im Anflug auf die Singularität
Das bloße Wissen, dass frei fallende Beobachter dort aufhören zu existieren (oder in der geometrischen Sprache der Allgemeinen Relativitätstheorie, dass ihre Weltlinien dort enden) gibt uns freilich nur sehr wenig Information über die Eigenschaften dieser Singularitäten. Einiges mehr lässt sich über diese merkwürdigen Objekte aber doch aussagen.
Eine wohlbekannte Auswirkung der Gravitation ist, dass sie Objekte komprimiert – Gravitation ist universell anziehend, und eine Wirkung des Gravitationsfeldes eines Objekts besteht darin, die einzelnen Bestandteile des Objekts möglichst nahe zueinander zu ziehen. Durch das Zusammenziehen wird die Gravitationswirkung stärker: Die Kraft, mit der beispielsweise ein Körper nahe der Sonnenoberfläche nach unten gezogen wird, ist zehntausend Mal schwächer als die Kraft, die ein Körper auf der Oberfläche eines Weißen Zwergsterns erfährt, der die gleiche Masse hat wie die Sonne, aber einen hundert Mal kleineren Durchmesser. Man könnte demnach auf den Gedanken kommen, eine durch Sternkollaps entstandene Singularität sei eine konsequente Fortsetzung dieses Zusammenhangs – mit einem zu immer größerer Dichte kollabierenden Sternrest, dessen Gravitationswirkung dementsprechend anwächst und zu noch stärkerer Verdichtung führt, bis sich Dichte und Gravitationsfeld in diesem Wechselspiel so aufgeschaukelt haben, dass sie unendliche Werte annehmen.
Tatsächlich ist ein solches Aufschaukeln für die Anfangsphasen des Kollapses charakteristisch, nicht aber für die weitere Entwicklung. Grund dafür ist, dass die Einsteingleichungen, die in der Allgemeinen Relativitätstheorie das Wechselspiel von Gravitation, Geometrie und Materie regeln, eine Eigenschaft besitzen, die in der Mathematik Nichtlinearität heißt. Übersetzt in die Physik bedeutet dies, dass Gravitation selbst Gravitationseffekte hervorrufen kann – Gravitation erzeugt weitere Gravitation! (Mehr Informationen hierzu bietet das Vertiefungsthema Die Gravitation der Gravitation.)
Sobald die Gravitation stark geworden ist, wirkt das Gravitationsfeld selbst als starke Gravitationsquelle, erzeugt damit ein noch stärkeres Gravitationsfeld, das dann seinerseits noch stärkere Gravitation hervorruft, bis die Gravitation letztendlich unendlich stark und die Singularität erreicht ist. Kommt man der Singularität nahe genug, dann wird der Beitrag der Gravitationswirkung der Gravitation weit wichtiger als die Gravitationswirkung der Materie – nahe der Singularität gilt in punkto Gravitation, dass es auf die Materie gar nicht mehr ankommt (viel schöner im Englischen: „near a singularity, matter doesn’t matter“).
Daraus folgt, dass sich die Physiker, die an den allgemeinen Charakteristika von Singularitäten interessiert sind, keine Gedanken über die möglichen Eigenschaften der Materie machen müssen, mit welcher der Kollaps seinen Ausgang nahm. Im Gegenteil ist es möglich, Singularitäten mit Hilfe vereinfachter Modelle zu erforschen, in denen gar keine Materie vorhanden sind, so genannter Vakuum-Lösungen der Einstein-Gleichungen. Die Hypothese, dass nahe einer Singularität nur das Gravitationsfeld selbst zählt, haben in den 1970er Jahren erstmals die sowjetischen Physiker Wladimir Belinskij, Isaak Chalatnikow und Jewgeny Lifschitz aufgestellt (heutzutage zusammenfassend zu BKL abgekürzt – wobei das K die englische Schreibweise von Khalatnikov wiederspiegelt).
Die drei Physiker stellten außerdem die Vermutung an, dass sich das Gravitationsfeld nahe einer Singularität mit der Zeit so schnell verändert, dass man die wichtigsten Eigenschaften dieser Regionen beschreiben kann, wenn man sich auf die Zeitabhängigkeit konzentriert und außer Acht lässt, wie die Gravitation von Ort zu Ort variiert. Zusammen sind die beiden Hypothesen – dass nahe der Singularität nur die Gravitation zählt, und dass es nur auf die Zeitabhängigkeit ankommt – als „BKL-Vermutung“ bekannt.
Gezeiten und Verformung
Wenn die Materie nahe der Singularität keine Rolle spielt – was dann? Die Kurzform der Antwort: zwei gravitationsbedingte Eigenschaften namens „Scherung“ und „Raumkrümmung“.
Scherung ist diejenige Eigenschaft der Gravitation, die dafür sorgt, dass ein Objekt, das in Richtung Singularität fällt, in unterschiedliche Richtungen unterschiedlich gestreckt oder gestaucht wird. Solche Verformungen sind ein Ausdruck von Gezeiteneffekten, wie sie bereits in der Newtonschen Gravitationstheorie auftreten. Beispielsweise werden ein überdimensionierter Wassertropfen oder eine Wolke von Staubteilchen, die auf die Erde zu fallen, in senkrechter Richtung gestreckt und in waagerechter Richtung gestaucht, wie in der nachfolgenden Animation zu sehen:
[Abbildung verwendet Daten von NASAs „Visible Earth“]

Zu der Streckung in vertikaler Richtung kommt es, da die Gravitationsanziehung mit zunehmendem Abstand von der Gravitationsquelle schwächer wird. Daher erfahren die unteren, erdnächsten Partien des Objekts eine etwas stärkere Anziehung als die oberen, erdferneren. In dem folgenden Bild zeigen die Längen der Pfeile, die von dem Objekt ausgehen, die relativen Stärken der Anziehungskraft an:
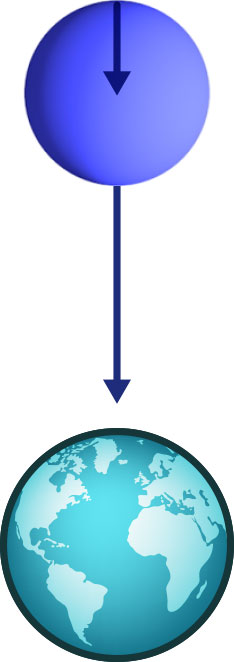
[Abbildung verwendet Daten von NASAs „Visible Earth“]
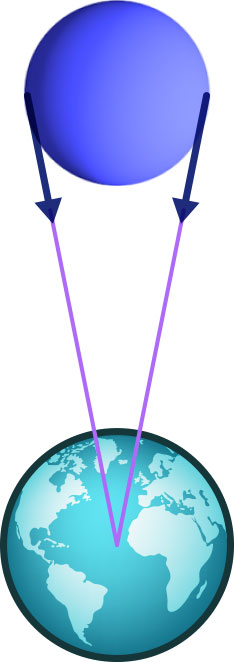
[Abbildung verwendet Daten von NASAs „Visible Earth“]
Scherung, Krümmung und Singularitäten
Genau wie ein Objekt, das auf die Erde zu fällt, wird ein Objekt, das in Richtung auf eine Singularität fällt in zwei Richtungen gestaucht und in der dritten gestreckt. Was die Erde betrifft, so ist die Scherung vergleichsweise schwach, und kleinere Festkörper – etwa eine Raumkapsel – werden nicht merklich verformt. Im Anflug auf eine Singularität dagegen wächst die Scherung immer weiter an, bis sie schließlich stärker wird als die inneren Kräfte, die Festkörpern ihre Formstabilität verleihen. Jedes Objekt, das sich der Singularität nähert, wird daher stark verformt und letztendlich sogar auseinandergerissen.
Die Scherung hat aber noch eine weitere Auswirkung – ein Musterbeispiel dafür, wie Gravitation weitere Gravitation hervorruft: Sie wirkt als Gravitationsquelle und bewirkt eine Krümmung des Raums. Diese Krümmung bewirkt ihrerseits, dass sich die Richtungen der Scherung drastisch ändern – ein Objekt, das eben noch in die senkrechte Richtung (die Fallrichtung) gestreckt und in waagerechter Ebene gestaucht wurde…
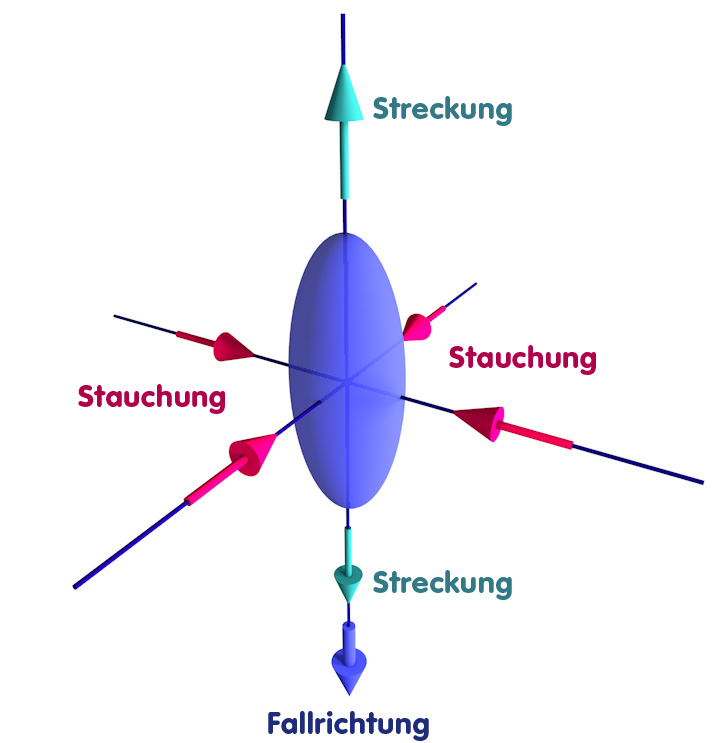
…kann im nächsten Moment bereits in senkrechter und in eine der waagerechten Richtungen gestaucht und in die andere waagerechte Richtung gestreckt werden:
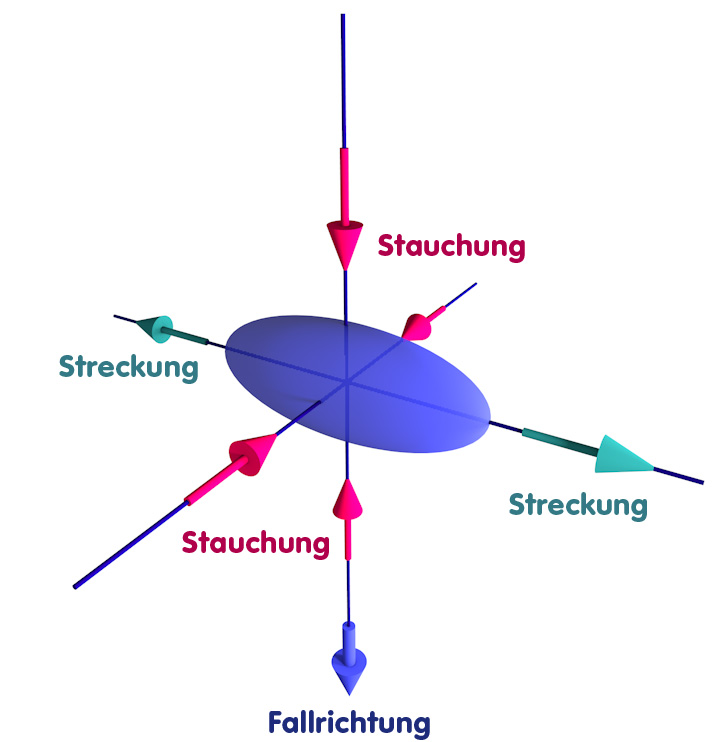
Das Endresultat ist ein Wechselspiel von starker Streckung und Stauchung in ständig wechselnden Richtungen, bei dem die Raumzeit ähnlich verzerrt wird wie Teig in einer Knetmaschine. Die nachfolgende Animation skizziert einen kleinen Ausschnitt aus der Sequenz der Streckungen und Stauchungen, denen ein Objekt auf dem Weg zur Singularität ausgesetzt ist:

[Animation nach Simulationsdaten von D. Garfinkle]
Aufgrund der Ähnlichkeit mit dem Kneten von Brotteig haben die Physiker für das Wechselspiel von Streckung und Stauchung den Fachausdruck „Mixmaster-Dynamik“ geprägt – benannt nach dem Mixmaster, einer in den USA weit verbreiteten Küchenmaschine, die sich unter anderem bei der Zubereitung von Brotteig einsetzen lässt.
Singularitäten im Computer
Belinskij, Chalatnikow und Lifschitz gewannen ihre grundlegenden Erkenntnisse über das Wesen der Singularitäten bereits in den 1970er Jahren. Der Nachweis, dass sie mit ihren Hypothesen richtig lagen, liegt dagegen nur einige Jahre zurück und beruht in weiten Teilen auf dem Einsatz numerischer Verfahren in der Relativitätsforschung (numerische Relativitätstheorie) – der Benutzung von Computersimulationen, um tiefere Einblicke in die mit Einsteins Relativitätstheorie verknüpfte Physik zu erlangen.
In solchen Forschungen verwendet man Computer, um die Eigenschaft bestimmter Modelluniversen zu simulieren, in denen die Gesetze der Allgemeinen Relativitätstheorie gelten. In den speziellen Simulationen, um die es hier geht, bekommt der Computer Daten über ein System, das gerade begonnen hat aufgrund der Gravitationswirkung seiner Materie zu kollabieren. Der Computer nutzt die Einsteingleichungen, um zu berechnen, wie sich dieses kollabierende System mit der Zeit weiterentwickelt. Dabei zeigt sich, dass das Gravitationsfeld und insbesondere seine Zeitentwicklung in der Endphase des Kollapses tatsächlich die maßgebliche Rolle spielen, und dass es außerdem zu dem von BKL vorhergesagten Wechsel von Streckung und Stauchung kommt. Die oben gezeigte Animation basiert auf Daten, die mit Hilfe solch einer Simulation gewonnen wurden.
Computersimulationen dieser Art sind Gegenstand der aktuellen Forschung, und eine Reihe wichtige Fragen sind noch offen. Beispielsweise ist bislang lediglich der Kollaps bestimmter Arten von Materie simuliert worden. Um zu zeigen, dass die Raumzeiteigenschaften nahe der Singularität wirklich von den Eigenschaften der kollabierenden Materie unabhängig sind, müsste man für möglichst viele und möglichst unterschiedliche Materieformen simulieren, was beim Kollaps passiert.
Die Simulation von Singularitäten ist eine echte Herausforderung – sie verlangt sowohl nach höchst effizienten Simulationsprogrammen wie auch nach einer beachtlichen Leistungsfähigkeit der verwendeten Computer. Um noch weiter in die Details der Entstehung von Singularitäten vordringen zu können, sind sowohl in punkto Programme als auch bei der Computertechnik noch deutliche weitere Fortschritte nötig. Als Belohnung dafür winken weitere interessante Einblicke in das Wesen von Singularitäten. Zum Beispiel besagt eine Vermutung der kanadischen Physiker Werner Israel und Eric Poisson, dass bei einem Gravitationskollaps, bei dem ein Schwarzes Loch entsteht, nur ein Teil der Singularität den von BKL vermuteten Eigenschaften genügt, während ein anderer Teil mit schwächeren Gezeitenkräften verbunden ist. Die Überprügung dieser Israel-Poisson-These ist eine der Herausforderungen, denen sich die Physiker mit zukünftigen, noch leistungsfähigeren Simulationen stellen sollten.
Die Quantennatur der Singularitäten
Folgt man allein den mathematischen Folgerungen aus der Allgemeinen Relativitätstheorie, dann wachsen bei Annäherung an die Singularität die Werte von physikalischen Größen wie Dichte und Raumkrümmung über alle Grenzen, und es kommt zu einer unendlichen Folge von raschen Richtungswechseln der Scherung. Allerdings treten nur vergleichsweise weniger dieser Richtungswechsel auf, bevor die Krümmung so gewaltige Werte annimmt, dass damit die Grenzen der Allgemeinen Relativitätstheorie erreicht sind: Bei so großer Krümmung spielen Quanteneffekte eine wichtige Rolle, und die entsprechenden Situationen können nur im Rahmen einer Theorie der Quantengravitation angemessen beschrieben werden. Dementsprechend werden wir die letzte Antwort auf das Wesen der Singularitäten erst mit Hilfe einer solchen Quantentheorie der Gravitation finden – und das heißt gleichzeitig, dass wir uns in Geduld üben müssen, denn obwohl bereits viel Arbeit investiert wurde, um eine solche Theorie zu entwickeln, sind die Forschungen noch nicht soweit fortgeschritten, dass sie tragfähige Aussagen über das Wesen der Singularitäten zuließen.
Weitere Informationen
Relativistische Hintergrundinformationen zu diesem Vertiefungsthema bietet unsere Einführung Einstein für Einsteiger, insbesondere das Kapitel Allgemeine Relativitätstheorie.
Verwandte Vertiefungsthemen finden sich in der Kategorie Allgemeine Relativitätstheorie.
Die Bilddaten für die Erdoberfläche, die in mehreren der Abbildungen dieses Vertiefungsthemas verwendet wurden, stammen vom NASA-Webportal Visible Earth.
Kolophon
David Garfinkle ist Professor für Physik an der Oakland University (USA) mit Forschungsschwerpunkt in der numerischen Relativitätstheorie.
Zitierung
Zu zitieren als:
David Garfinkle, “Singularitäten als Raumzeit-Knetmaschinen” in: Einstein Online Band 03 (2007), 03-1103










