Das Singularitäten-Theorem (Physiknobelpreis 2020)

Roger Penrose erhielt 2020 eine Hälfte des Nobelpreises für Physik. Er hatte gezeigt, dass Schwarze Löcher eine robuste Vorhersage der Allgemeinen Relativitätstheorie sind.

Ein Artikel von Emanuel Malek

Der britische Physiker und Mathematiker Roger Penrose erhielt 2020 eine Hälfte des Nobelpreises für Physik für die Entdeckung, dass die Entstehung Schwarzer Löcher eine robuste Vorhersage der Allgemeinen Relativitätstheorie ist.

Seit der Formulierung 1916 hat Einsteins Relativitätstheorie Physikerinnen und Physiker immer wieder überrascht und in Verlegenheit gebracht. Beispielsweise sind dieser Theorie nach Raum und Zeit nicht absolut und fest, sondern werden durch Masse und Energie verzerrt. Diese Raumzeitkrümmung bringt die Gravitationskraft hervor. Seit 1960 haben sich die meisten Physikerinnen und Physiker mit den revolutionären Eigenschaften der Allgemeinen Relativitätstheorie angefreundet – mit Ausnahme einer ihrer seltsamsten Vorhersagen, der Existenz Schwarzer Löcher. Hier ging die Debatte weiter.

Das Ende der Raumzeit

Die Gleichungen, die die Allgemeine Relativitätstheorie beschreiben, haben auch mathematische Lösungen in Situationen, in denen Materie so dicht in eine kleine Raumzeitregion gepackt ist, dass nichts – nicht einmal Licht – daraus entkommen kann. Solch eine Region bezeichnen Wissenschaftlerinnen und Wissenschaftler als Schwarzes Loch. Der sogenannte Ereignishorizont trennt das Schwarze Loch vom Rest der Raumzeit. Laut Allgemeiner Relativitätstheorie kann nichts, was den Ereignishorizont überschreitet, jemals wieder entkommen. Es wird unwiederbringlich in das Zentrum des Schwarzen Lochs fallen. Hinter dem Ereignishorizont gibt es also kein Zurück.

Was die Schwarzen Löcher noch lästiger macht, ist, dass man tief darin eine Singularität vorfindet, und das jedes Objekt, das in das Schwarze Loch fällt, früher oder später diese Singularität erreicht. Dort wird das Gravitationsfeld unendlich stark – es zerreißt die Raumzeit selbst. Laut der Mathematik der Allgemeinen Relativitätstheorie hört alles, was die Singularität erreicht, also auf zu existieren – eine äußerst problematische Konsequenz für die physikalische Welt.

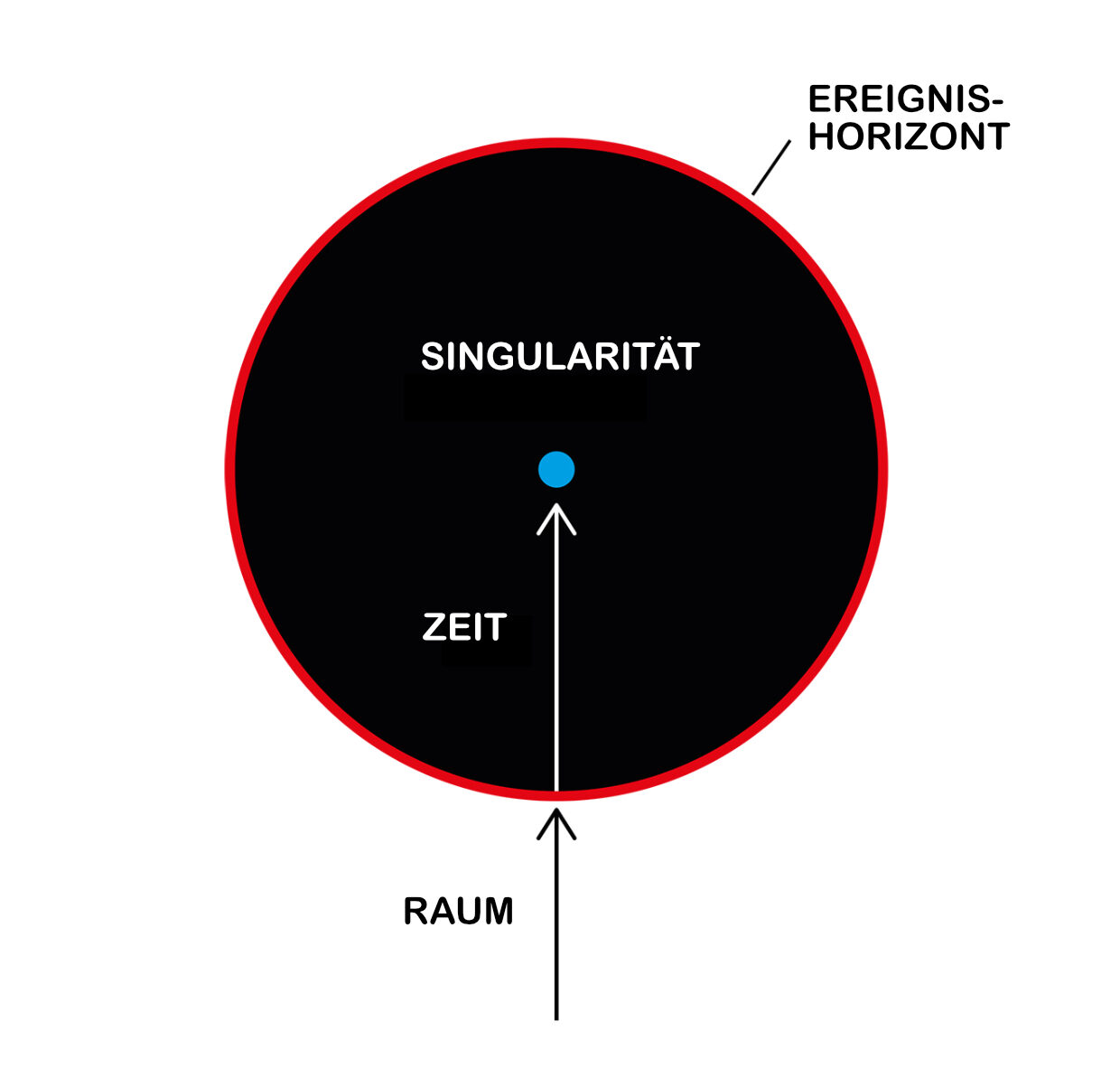
Darstellung eines Schwarzen Lochs mit einer in ihm liegenden Singularität. ©Johan Jarnestad/The Royal Swedish Academy of Sciences

Mathematisches Artefakt oder physikalische Vorhersage?

Diese pathologische Natur der Singularität – der Umstand, dass Raum und Zeit darin verschwinden, ist ein sehr bedauerlicher Zug der Allgemeinen Relativitätstheorie. Allerdings war es bis zu Penroses Arbeit auch unklar, ob Schwarze Löcher und Singularitäten wirklich existieren, oder ob sie einfach mathematische Artefakte der Theorie sind. Tatsächlich benötigten bis dahin alle rechnerischen Lösungen für Schwarze Löcher eine perfekt symmetrische Anordnung der Materie, was in der Natur so nicht vorkommen kann.

Viele Physikerinnen und Physiker glaubten deshalb lange Zeit, dass Schwarze Löcher in der realen Welt gar nicht auftreten. Man überlege, wie ein Schwarzes Loch in der Natur entstünde: Um einen Gravitationskollaps herbeizuführen, bräuchte es genügend Materie und Energie, die sich in einer begrenzten Region der Raumzeit sammelte, sodass die Gravitationskraft größer würde als jeder Druck oder andere Abstoßung. Die Gravitationskraft würde dabei so dominant, dass die ganze Materie auf noch kleinerem Raum zusammengepfercht würde, bis ein Schwarzes Loch entstünde. Zwar wurde solch ein theoretischer Prozess des Gravitationskollaps zum Schwarzen Loch bereits 1939 von Robert Oppenheimer und Hartland Sweet Snyder beschrieben. Sie nahmen jedoch an, dass die Materie aus einem idealen Staub besteht, der keinen Druck ausübt, und dass sie perfekt kugelsymmetrisch angeordnet ist. Tatsächlich würde man solch ideale Bedingungen in der Natur niemals antreffen.

Könnte es also sein, dass die kleinste Störung der Kugelsymmetrie oder der kleinste Druck genügte, um die Entstehung eines Schwarzen Lochs aufzuhalten? Man könnte doch argumentieren, dass die Materie bei der kleinsten Abweichung von der Kugelsymmetrie nicht mehr auf einen Punkt kollabieren würde, sondern dass die Materie gewissermaßen auf einer Seite überschwappte und so den ganzen Kollaps verhinderte. Könnte außerdem der kleinste Druck genügen, die Entstehung der Singularität aufzuhalten? Die schwierige Natur der Gleichungen und das Fehlen moderner Rechenleistung erschwerte die Beantwortung dieser Fragen.

Penroses Singularitäten-Theorem

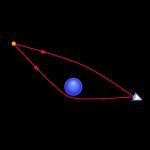
Penrose bewies, dass sich Singularitäten – und damit auch Schwarze Löcher – ganz generell aus der Allgemeinen Relativitätstheorie ergeben, ohne dass man stringente Symmetrien annehmen müsste und für ganz allgemeine Eigenschaften der Materie. Penroses Kernidee war, sich anzuschauen, wie die Gravitationskraft Licht beeinflusst. In der Allgemeinen Relativitätstheorie wirkt die Gravitationskraft auch auf Licht und zwingt es zur Abweichung von einem sonst geraden Weg. Ein schweres Objekt wirkt als Gravitationslinse auf Lichtstrahlen. Ähnlich wie eine optische Linse fokussiert die Gravitationskraft die Lichtstrahlen auf eine Art Brennpunkt.

Ist die Gravitationskraft stark genug, führt der Gravitationslinseneffekt dazu, dass eine Oberfläche in der Raumzeit eingeschlossen wird. Es handelt sich um eine zweidimensionale geschlossene Fläche ähnlich einer Kugel, sodass alle Lichtstrahlen, die senkrecht zur Oberfläche einfallen, konvergieren. Dies steht im Kontrast zu einer Kugeloberfläche in der flachen Raumzeit, wo nach außen gerichtete Lichtstrahlen divergieren. Anders gesagt: Wegen des Gravitationseffekts kann Licht der eingeschlossenen Oberfläche niemals entkommen.

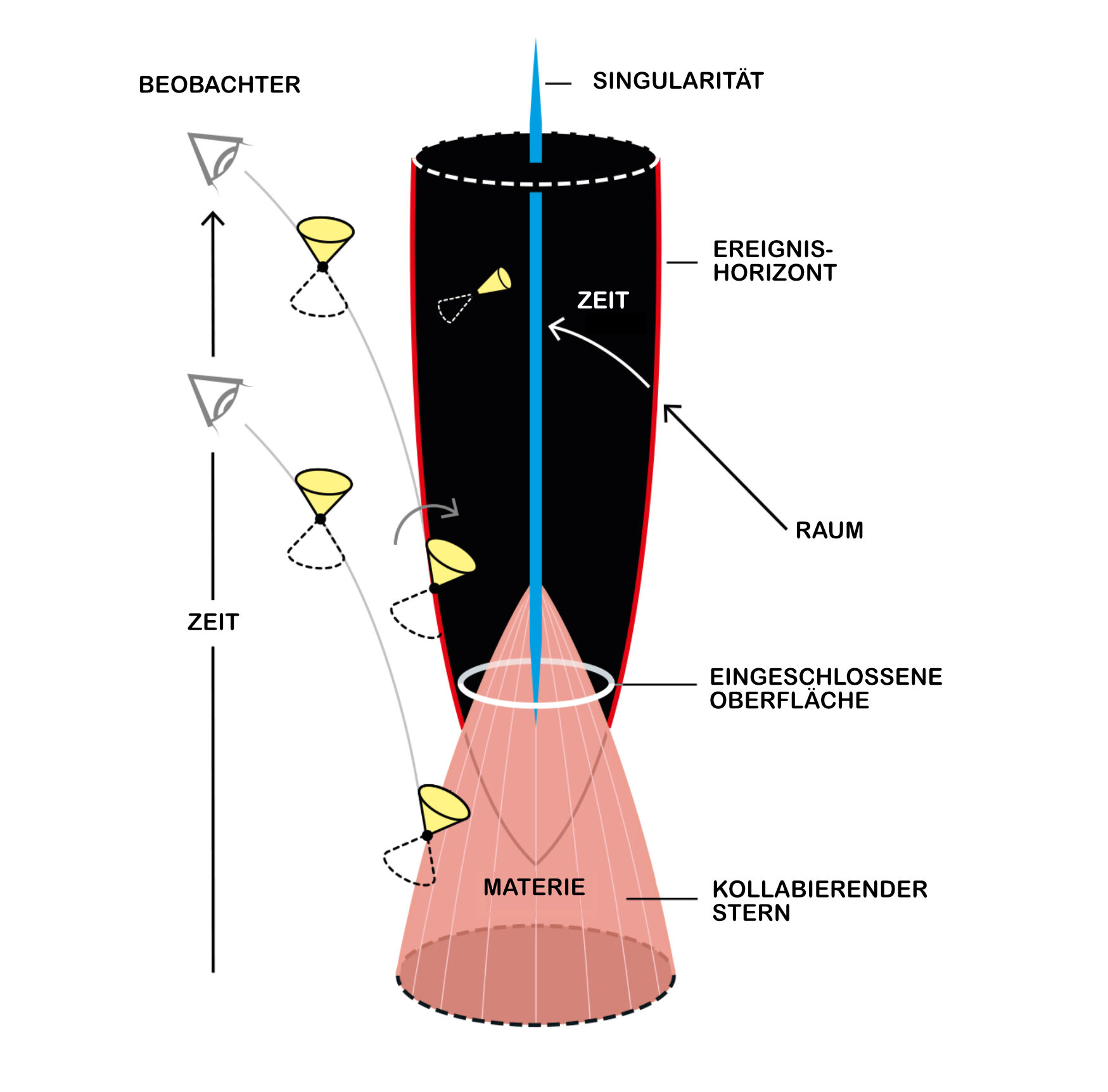
Darstellung des Gravitationskollaps und der Entstehung einer Singularität. Die Illustration ist einer Grafik von Roger Penrose nachempfunden. ©Johan Jarnestad/The Royal Swedish Academy of Sciences

Penrose zeigte für die sogenannte schwache Energiebedingung, also wenn alle Materie eine positive Energiedichte hat, dass eine eingeschlossene Oberfläche notwendigerweise eine Raumzeitsingularität beinhaltet. Er machte also nur eine minimale Annahme für die Materie in der Raumzeit und schloss, dass die Entstehung einer Singularität die unvermeidliche Folge einer eingeschlossenen Oberfläche ist. Das bedeutet auch, dass es in der Allgemeinen Relativitätstheorie ganz generell zu Singularitäten kommt, auch ohne spezielle Symmetrien. Im Beispiel des kugelsymmetrischen Kollaps von Oppenheimer und Snyder gibt es also eine eingeschlossene Oberfläche, die auch Abweichungen von der kugelsymmetrischen Anordnung überdauert.

Die Natur der Raumzeit-Singularität

Die Stärke von Penroses Argument liegt in seinen minimalen Annahmen – die Existenz eingeschlossener Oberflächen und die schwache Energiebedingung. Dadurch lässt sich das Singularitäten-Theorem sehr breit anwenden und zeigt, dass viele Situationen in der Allgemeinen Relativitätstheorie Singularitäten hervorbringen. Allerdings verrät das Singularitäten-Theorem aufgrund seiner Allgemeinheit auch erstmal nichts weiter über die Singularität, abgesehen von ihrer Existenz. Tatsächlich zeigt Penroses Argument auch nicht, dass eine Singularität notwendigerweise von einem Ereignishorizont, also einem Schwarzen Loch, umgeben ist.

In gewisser Weise hat Penroses Singularitäten-Theorem der Allgemeinen Relativitätstheorie noch unverständlichere Phänomene entlockt. Es hat gezeigt, dass Singularitäten eine robuste Vorhersage der Allgemeinen Relativitätstheorie sind und sich nicht einmal in Schwarzen Löchern verstecken müssen. Es scheint also, als hätte die Raumzeit ganz allgemein Löcher, wo Raum und Zeit enden und physikalische Gesetze versagen: nackte Singularitäten.

Um dieser absurden Vorstellung etwas entgegenzusetzen, formulierte Penrose seine Vermutung der kosmischen Zensur. Demnach sind alle Raumzeitsingularitäten hinter einem Ereignishorizont verborgen. Das würde den Rest der Raumzeit vor den verheerenden Konsequenzen einer Singularität durch einen Ereignishorizont abschirmen. Obwohl diese Annahme breite Zustimmung findet, scheint sie äußert schwer zu beweisen zu sein und ist daher weiterhin Gegenstand der Forschung. Ein Problem ist dabei, die Vermutung so zu formalisieren, dass sie bewiesen oder widerlegt werden kann, ohne dass man gleich Gegenbeispiele findet.

Die Urknall-Singularität und Quantengravitation

Penroses Singularitäten-Theorem hat viele Entwicklungen in der Allgemeinen Relativität angestoßen. Beispielsweise verallgemeinerte Penrose zusammen mit Stephen Hawking sein Singularitäten-Theorem, um es auf das ganze Universum anwenden zu können. So konnten die beiden Physiker zeigen, dass in der Vergangenheit unseres Universums selbst eine Singularität liegt, von der im Urknall alle Materie und Energie ausging.

Der Umstand, dass Singularitäten ganz allgemein aus Einsteins Theorie der Allgemeinen Relativität hervorgehen, hat die Suche nach einer Theorie der Quantengravitation – wie etwa die String-Theorie – weiter angespornt. Sie soll Einsteins Theorie auf kleine Skalen erweitern und mit der Quantenmechanik in Einklang bringen. Die Hoffnung ist außerdem, dass solch eine Theorie die Raumzeitsingularitäten beseitigen würde, die sich derzeit noch im Inneren der Schwarzen Löcher eingenistet haben.

Weitere Informationen