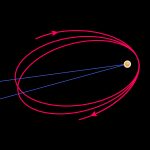
Eine subtile Richtungsänderung: geodätische Präzession

In Albert Einsteins Allgemeiner Realtivitätstheorie besteht ein direkter Zusammenhang zwischen Gravitation und der Geometrie von Raum und Zeit. Dieser Text erkundet, was die Krümmung der Raumzeit ist und wie sie mit Hilfe von Kreiseln vermessen werden kann.

Ein Artikel von Markus Pössel

In Albert Einsteins Allgemeiner Relativitätstheorie besteht ein direkter Zusammenhang zwischen der Gravitation und der Geometrie von Raum und Zeit. Insbesondere ist die Raumzeit in der Umgebung eines massereichen Körpers verzerrt. Dort unterscheidet sich beispielsweise die Geometrie des Raumes von der gewöhnlichen Euklidischen Geometrie, wie sie in der Schule unterrichtet wird. Eine Konsequenz daraus betrifft die Möglichkeit, die Orientierung von Objekten zu beurteilen, die sich in einem gewissen Abstand zueinander befinden. Zeigen beispielsweise zwei pfeilförmige Objekte, auch „Vektoren“ genannt, in dieselbe Richtung oder nicht? Geht man dieser Frage nach, kann man auf eine Definition stoßen, was die Krümmung von Flächen, Räumen oder der Raumzeit eigentlich ist. Außerdem ergeben sich aus diesen Überlegungen interessante Möglichkeiten, die Verzerrung der Raumzeit experimentell nachzuweisen.

Pfeile vergleichen: Parallelverschiebung

Die vierdimensionale, gekrümmte Raumzeit lässt sich nicht in einfacher Weise veranschaulichen. Glücklicherweise kann man für viele Aspekte ihrer Geometrie aber bereits dann ein Gefühl bekommen, wenn man einfachere Gebilde betrachtet – zum Beispiel zweidimensionale Oberflächen.

Stellen wir uns vor, wir schauten auf eine zweidimensionale Ebene, in der zwei pfeilförmige Objekte, zwei Vektoren liegen. Zeigen die beiden Pfeile in die gleiche Richtung? Allgemeiner: Wie können wir überhaupt feststellen, ob sie in dieselbe Richtung zeigen?

Im einfachsten Fall befinden sich die Fußpunkte der Pfeile am selben Ort. Dann können wir direkt den Winkel zwischen den beiden Pfeilschäften messen. Ist der Winkel Null, dann zeigen die beiden Pfeile in die gleiche Richtung:

Was aber, wenn die Fußpunkte nicht übereinstimmen? Normalerweise haben wir selbst dann keine Probleme, die Richtung einzuschätzen. Wir müssen uns nur vorstellen, wie der erste Pfeil aussehen würde, wäre er zum Ort des zweiten Pfeiles verschoben: würden die Pfeilschäfte dann zusammenfallen?

Nun müssen wir nur noch definieren, wie wir den Pfeil für diesen Vergleich verschieben sollten, so dass sich seine Richtung während der Verschiebung nicht ändert. In der Ebene ist die Vorgehensweise dabei recht einfach: Man zeichne eine Gerade vom ursprünglichen Fußpunkt des Pfeiles hin zu dem Punkt, an den man den Fußpunkt verschieben möchte. Dann wird der Pfeil entlang dieser Gerade so verschoben, dass der Winkel zwischen Pfeilschaft und Gerade während der gesamten Verschiebung konstant bleibt. Das ist in der folgenden Animation dargestellt:

Nach der Verschiebung können die beiden Pfeile dann  direkt miteinander verglichen werden, da ihre Fußpunkte dann zusammenfallen.

Verschiebung entlang eines geschlossen Wegs

Was ist mit Verschiebungen entlang komplizierterer Wege, beispielsweise entlang einer Kombination verschiedener Geradenabschnitte? Im Falle einer Ebene sich heraus, dass wir jeden beliebigen Weg nehmen können, um vom alten zum neuen Fußpunkt zu kommen. Das Ergebnis wird in allen Fällen dasselbe sein.

Dass die Richtung des verschobenen Pfeils nicht davon abhängt, welchen Weg wir genommen haben, lässt sich auch anders ausdrücken. Es ist gleichwertig zu der Aussage, dass ein Pfeil, den wir entlang eines geschlossenen Wegs verschieben, nach Ende seiner Rundreise genau in dieselbe Richtung zeigt wie zuvor:

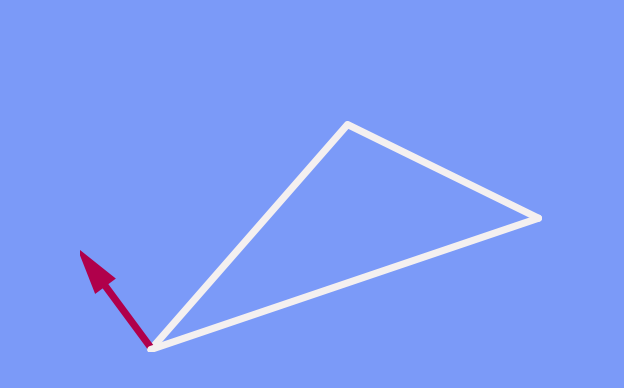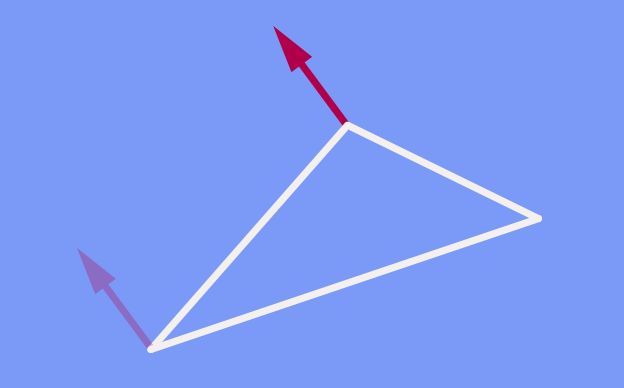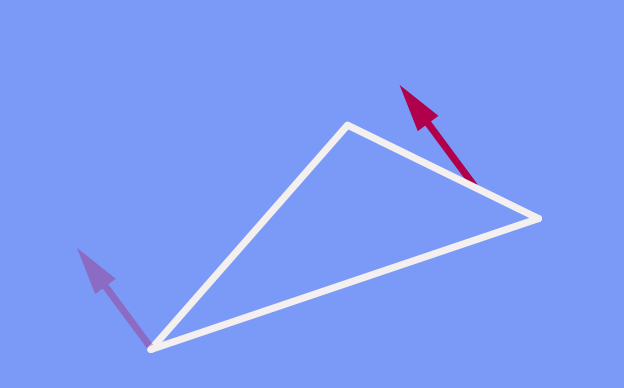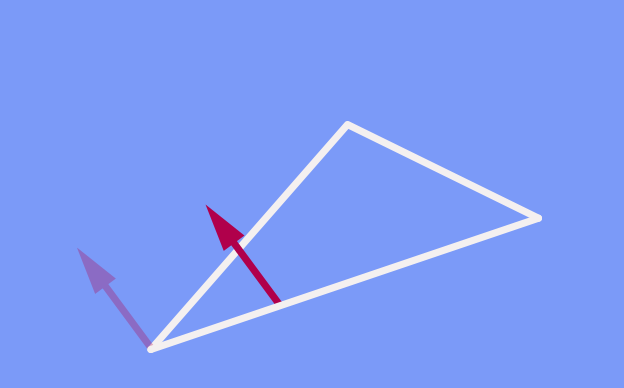
Sie fragen sich an dieser Stelle womöglich, warum ich diesen Umstand überhaupt erwähnenswert finde. Ist es nicht offensichtlich, dass ein Pfeil beim Verschieben entlang eines geschlossenen Weges seine Richtung beibehält, solange man jeweils darauf achtet, dass der Winkel zwischen Pfeil und Wegabschnitt konstant bleibt? In der Ebene (und im gewöhnlichen, alltäglichen, dreidimensionalen Raum) ist dies der Fall. Aber die Lage ändert sich, sobald Krümmung ins Spiel kommt.

Pfeile auf einer gekrümmten Oberfläche

Betrachten wir deswegen nicht mehr eine Ebene, sondern die gekrümmte Oberfläche einer Kugel. Eine Richtung auf einer solchen Kugel (wie zum Beispiel Norden, Süden, Osten, Westen und die vielen anderen Richtungen dazwischen, die hier auf der Erde definiert sind) kann durch einen Vektor dargestellt werden, der tangential zur Kugeloberfläche ist.

Dazu legt man an jedem Punkt der Oberfläche eine sogenannte „Tangentialebene“ an: eine ebene Fläche, die sich an diesem einen Punkt so eng wie möeglich an die gekrümmte Oberfläche anschmiegt. Hier ist ein Beispiel; zusätzlich zu einem quadratischen Ausschnitt aus der Tangentialebene habe ich einen Pfeil (einen Vektor) eingemalt, der in der Tangentialebene liegt:

Lassen Sie uns etwas näher gehen…

.. und die Ebene von der Seite betrachten:

Die Ebene ist, weil wir direkt von der Seite sehen, nur noch als dünne Linie sichtbar. Ebene und Vektor liegen, wie man hier sehen kann, in der Tat tangential zur Kugeloberfläche.

Pfeiltransport auf der Kugelfläche

Nachdem wir Tangentialebenen definiert haben, und außerdem die Pfeile, die in ihnen leben, stellt sich nun die Frage, wie wir diese Pfeile auf der Kugeloberfläche verschieben können, ohne dass ihre Richtung sich ändert. Es gibt auf einer solchen Kugeloberfläche zwar keine Geraden. Aber es gibt Wege, die so gerade wie irgend möglich verlaufen. Das sind die sogenannnten Großkreise (oder Abschnitte davon). In der üblichen Darstellung einer Kugelfläche im dreidimensionalen Raum haben Großkreise den gleichen Mittelpunkt und den gleichen Radius wie die Kugelfläche. Beispiele auf der Erdkugel sind der Äquator (Großkreis) und die Meridiane, die von Pol zu Pol verlaufen (Großkreisabschnitt).

Dass Geraden in diesem Falle durch Großkreise ersetzt werden, die den geradestmöglichen Wegen auf der Kugeloberfläche entsprechen, legt folgende Abänderung unserer Vorschrift nahe, Pfeilrichtungen miteinander zu vergleichen: Wir verschieben den Fußpunkt unseres Pfeils entlang eines Weges, der aus Großkreisabschnitten zusammengesetzt ist, und achten dabei sorgfältig darauf, dass entlang jedes kleinen Wegstücks der Winkel zwischen dem Pfeil und der Wegrichtung derselbe bleibt. Mehr können wir nicht tun – näher als so können wir der Definition des Paralleltransports, die wir in der Ebene gewählt hatten, nicht kommen.

Eine Kugelfläche stellen wir uns meistens so vor, wie wir es aus dem Alltag gewohnt sind – als Oberfläche einer Kugel, die in den gewöhnlichen, dreidimensionalen Raum eingebettet ist. Aber diese dreidimensionale Einbettung ist lediglich eine Möglichkeit, die Kugeloberfläche zu veranschaulichen.  Das, woran wir interessiert sind, nämlich die Richtung und die Verschiebung von Pfeilen, betrifft nur die zweidimensionale Kugeloberfläche und nicht den umgebenden Raum. Falls wir den Pfeil, wie gerade geschildert, parallelverschieben, dann gilt insbesondere nicht, dass er im dreidimensionalen Umgebungsraum seine Richtung beibehielte. Im Gegenteil: Entlang des Weges krümmt sich die Oberfläche vom dreidimensionalen Raum aus gesehen nach unten weg. Der Pfeil muss deswegen notwendigerweise seine Richtung ändern, um dieser Krümmung zu folgen, damit er weiterhin tangential zur Kugeloberfläche stehen kann.

Richtungsänderung durch Krümmung: ein drastisches Beispiel

Nach diesen Vorbereitungen zurück zu der Frage, was mit einem Pfeil passiert, der auf der Kugeloberfläche entlang eines geschlossenen Weges transportiert wird. Betrachten wir einen einfachen Fall eines solchen Weges, nämlich ein Dreieck aus Großkreisabschnitten. Für ein normales Dreieck in der Ebene hatten wir in einer Animation gesehen, dass sich die Richtung des Pfeils beim Rundtransport nicht ändert.

In der nachfolgenden Animation ist nun ein Beispiel für einen Pfeiltransport entlang eines Dreiecks auf der Kugelfläche dargestellt. Die Dreiecksseiten sind sämtlich Abschnitte von Großkreisen. Wir starten am Äquator mit einem nach Westen zeigenden Pfeil und verschieben diesen zunächst entlang eines Meridians zum Nordpol verschieben. Anschließen bewegen wir den Pfeil entlang eines anderen Meridians wieder zurück zum Äquator, um ihn dann entlang eines Äquatorabschnitts zurück zu seinem Ausgangspunkt zu verschieben:

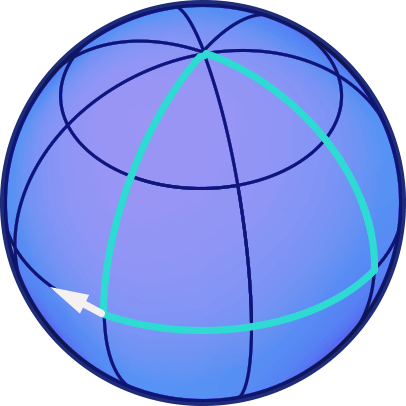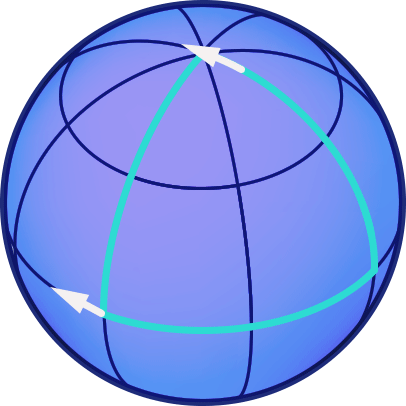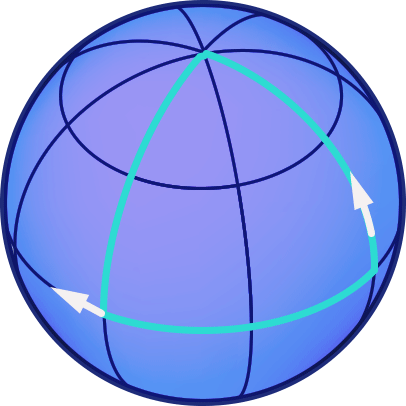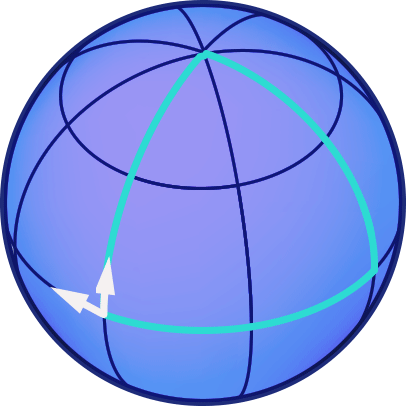
In diesem Fall ergibt sich am Ende der Rundreise ein Winkel von 90 Grad zwischen der Richtung des Pfeiles vor seiner Reise und seiner Richtung, nachdem er verschoben wurde. Macht man den gleichen Versuch mit verschiedensten Rundwegen auf der Kugel, dann stellt man fest, dass der Winkel, um den sich der Pfeil nach seiner Reise relativ zu seiner Ausgangsrichtung gedreht ist, sowohl zu der Fläche proportional ist, die der Weg einschließt, als auch zum Kehrwert des Kugelradius. Der Radius ist nun aber ein Maß für die Krümmung der Kugel: Die Oberfläche einer Kugel mit großem Radius ist nur leicht gekrümmt. Nimmt man zum Beispiel denjenigen Teil der Erdoberfläche, den wir in unserem alltäglichen Leben überschauen können, so scheint dieser fast flach (also gar nicht gekrümmt) zu sein. Je kleiner der Radius einer Kugel, desto größer ist ihre Krümmung.

Krümmung definieren

Bei der Kugel mag mit dem Kugelradius ein natürliches direktes Maß für die Krümmung zur Verfügung stehen. Im allgemeinen, und insbesondere bei mehr als zwei Dimensionen, ist die Situation deutlich komplizierter. Hier helfen die Vorstellungen vom Paralleltransport kleiner Pfeile, eine allgemeine Definition für die Krümmung zu finden, die sich auf Räume beliebiger Dimension anwenden lässt.

Dazu betrachtet man einen beliebigen Punkt P in dem betreffenden Raum und wählt drei Richtungen aus: zwei Richtungen, die anschließend Wege definieren, und eine Richtung, die dem von uns schon betrachteten Pfeil entspricht. Nun verschiebt man den Pfeil zunächst um eine kleine Distanz d in die erste Richtung und anschließend um eine kleine Distanz D in die zweite. Dabei vergewissert man sich, dass der Weg, entlang dem man diese Verschiebung vornimmt, so gerade und die Richtung des Pfeils so konstant wie möglich gehalten werden.

Anschließend führt man die Verschiebungen erneut durch, jedoch in einer anderen Reihenfolge: Nun verschiebt man den Vektor zunächst entlang der zweiten Richtung gefolgt von einer Verschiebung in die erstere, gerade so, dass man eine Art Parallelogramm erhält. Es folgt eine Animation des Vorgangs:

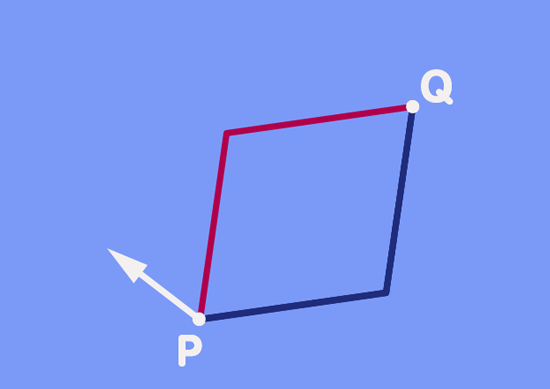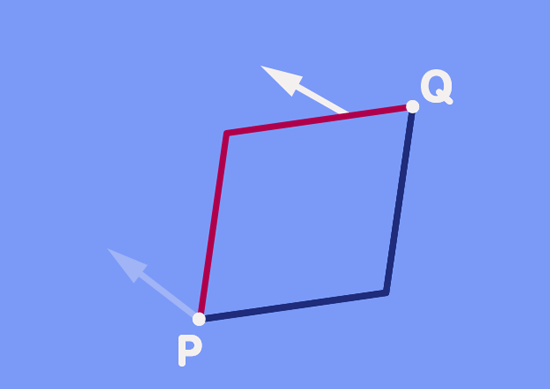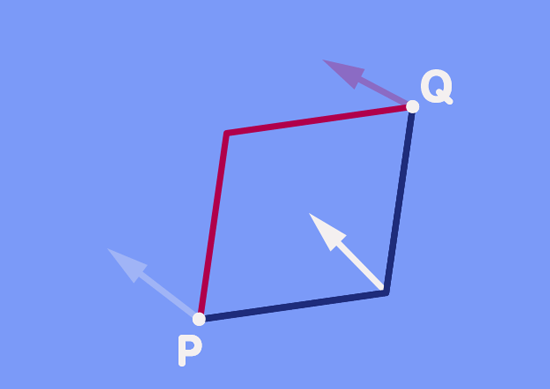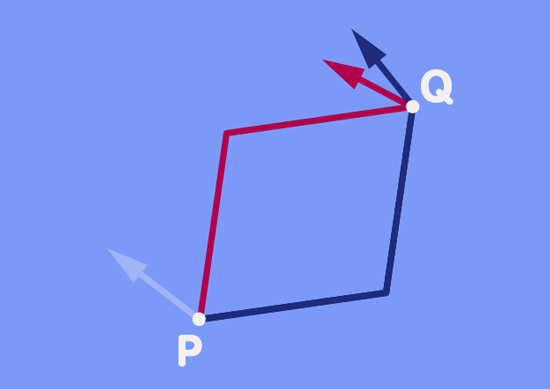
Vor dem Hintergrund, was Sie schon über die feinen Richtungsänderungen auf einer Kugeloberfläche gelesen haben, werden Sie nicht allzu überrascht über das Ergebnis sein, das in der Animation veranschaulicht wird: Im Allgemeinen wird sich die Richtung des Vektors, der entlang des einen Weges verschoben wurde, unterscheiden von der Richtung des anderen Vektors, der entlang des anderen Weges verschoben wurde.

Tatsächlich ist das Verschieben des gleichen Vektors entlang zweier verschiedener Wege zu einem anderen Punkt das gleiche, als wenn man den Vektor entlang eines geschlossenen Weges verschiebt. Man beginnt mit dem grünen Vektor, so wie er in Punkt Q gezeigt wird. Verschiebt man diesen zurück zu Punkt P, so würde dies in den ursprünglichen Vektor resultieren. Nochmaliges Verschieben dieses ursprünglichen Vektors entlang des roten Weges zurück zu Q führt zu dem roten Vektor, der auch in Punkt Q dargestellt wird. Der Richtungsunterschied der Vektoren in Punkt Q ist tatsächlich der Gleiche, den wir erhalten hätten, wenn wir einen von beiden entlang des geschlossenen Weges, gegeben durch das Parallelogramm, bewegt hätten.

Dieses kleine Szenario steht im direkten Zusammenhang mit der mathematischen Definition des Standardmaßes für Krümmung, das auf den imposanten Namen „Riemannscher Krümmungstensor“ hört. Der Riemannsche Krümmungstensor ist eine Funktion – wenn man will eine mathematische Maschiene, in die man eine Anzahl von mathematischen Objekten eingeben kann, um diese weiterzuverarbeiten zu einem speziefischen Ergebnis. Um konkreter zu werden: Gibt man in den Krümmungstensor sämtliche Informationen über die kleine, oben dargestellte Parallelogrammskizze – einen bestimmten Punkt im Raum, den Vektor, den man verschieben möchte, die zwei Richtungen und die zwei Weglängen d und D – so würde dieser als Resultat den Unterschied zwischen dem grünen und dem roten Vektor im Punkt Q ausgeben.

Im Falle der zweidimensionalen Kugel(oberfläche) hängen die erhaltenen Unterschiede von der Fläche, die von der Wegstrecke eingeschlossen wird, und einer einzigen Zahl, die das Krümmungsverhalten charakterisiert, sprich dem Radius der Kugel, ab. In höherdimensionalen Räumen gibt es mehr Möglichkeiten unterschiedliche Richtungen zu wählen – sowohl für die Orientierung des kleinen Parallelogramms als auch für die Wahl des Vektors – als in einer zweidimensionalen Oberfläche. Entsprechend wird das Krümmungsverhalten in einem Punkt nicht nur von einer Größe bestimmt, sondern von von n²·(n²-1)/12 Größen. Die Krümmung eines jeden Punktes in einer vierdimensionalen Raumzeit – ein wesentlicher Bestandteil für die Formulierung der Allgemeinen Relativitätstheorie – wird durch 20 Zahlen charakterisiert.

Kreisel in der Raumzeit

Aber nun zurück zu Dingen, die etwas weniger abstrakt sind. In der Raumzeit gibt es eine ziemlich konkrete Realisierung von Vektoren und wie man diese verschiebt, während ihre Richtung so konstant wie möglich bleibt: Kreisel!

Im tiefen Weltall, weit weg von allen äußeren Einflüssen, behält die Achse eines Kreisels seine Richtung bei:

Diese Richtungserhaltung steht in direktem Zusammenhang zu einem physikalischen Gesetz, das die Drehmomenterhaltung regelt und das aussagt, dass die Richtung der Drehachse konstant bleibt (Hintergurndinformationen über das Drehmoment kann im Vertiefunsthema Was Eiskunstläufer, Planeten und Neutronensterne gemeinsam haben gefunden werden.), es sei denn, der Kreisel interagiert mit seiner Umgebung.

Auf der Erde kann man versuchen eine solche interaktionsfreie Umgebung nachzustellen, indem man den Kreisel in eine kardanische Aufhängung platziert – eine spezielle Anordnung von rotierenden Ringen, die den Kreisel seine Richtung beibehalten lassen, sogar dann, wenn die Orientierung des Fußpunktes, an dem dieser festgemacht ist, sich ändert.

Anspruchsvollere Versionen dieser Anordnung sind die Grundlage für (mechanische) Kreiselkompasse, die seit Mitte des 19. Jahrhunderts auf Schiffen benutzt werden. Wenn die Rotationsachse anfänglich zum Nordpol ausgerichtet wurde, so zeigt sie auch weiterhin nach Norden, sogar dann, wenn das Schiff einen anderen Kurs einschlägt. Eine andere Anwendung jenes „Trägheitsnavigationsequipments“ ist bei Flugzeugen oder Raketen, wo ein Satz von Kreiseln einen Satz von Bezugsrichtungen liefert, mit denen die Orientierung von Flugzeugen oder Raketen im All festgestellt werden kann.

Geodätische Präzession

In all diesen Anwendungen wird angenommen, dass das Bewegen eines Kreisels nicht dessen Ausrichtung ändert. Während dies im Kontext der klassischen Mechanik und sogar in der Speziellen Relativitätstheorie richtig ist, stellen sich die Dinge in der Allgemeinen Relativitätstheorie nicht ganz so einfach dar, da hier die Gravitation ins Spiel kommt. Dennoch gibt es einen einfachen Weg, einen Vektor, repräsentiert durch die Achsen eines rotierenden Kreisels, zu verschieben: Einfach loslassen! Genauer: Ein Kreisel im freien Fall ist in der Allgemeinen Relativitätstheorie das Äquivalent zu der Verschiebung eines Vektors mit so wenig Richtungsänderungen wie möglich – das Analogon zu unserer Vektorverschiebung in einer Ebene und auf der Kugeloberfläche.

Aber die Verschiebung eines Vektors mit so wenig Richtungsänderungen wie möglich bedeutet nicht, dass es überhaupt keine Änderungen gibt. Dort, wo die Raumzeit gekrümmt ist (insbesondere in der Nähe von Masse), gibt es eine feine Richtungsänderung – wie im Falle unserer gekrümmten Kugeloberfläche.

Man stelle sich hierzu einen Kreisel vor, der sich 640 Kilometer über der Erdoberfläche im freien Fall um Selbige befindet und einen geschlossenen, kreisförmigen Orbit verfolgt, wie es in der folgenden Animation dargestelllt wird. An einem bestimmten Punkt auf seiner Umlaufbahn setzt man die Achse des Kreisels so fest, dass diese parallel zu dem Licht verläuft, das von einem bestimmten, weit entferntem Stern, einem Bezugsstern, empfangen wird:

Wie man hier sehen kann, unterscheidet sich die Orientierung des Kreisels, nachdem dieser einen Umlauf vervollständigt hat, leicht von der Anfänglichen, was sich durch einen Vergleich mit dem Licht des Bezugssterns feststellen lässt.

Die Verschiebung in die Richtung seiner Achse ist minimal. Für einen Kreisel auf einer kreisförmigen Umlaufbahn, 640 Kilometer über der Erdoberfläche, würde sich die Achse um den 340 milliardsten Teil eines Grades pro Umlauf ändern (dies entspricht einer Drehung um 6,7 Arksekunden pro Jahr). Um diese Verschiebung in der Animation sichtbar zu machen, wurde Sie um den Faktor 50 Millionen vergrößert.

Dieser Effekt wird geodätische Präzession genannt. Im Allgemeinen beschreibt Präzession die Richtungsänderung der Rotationsachse eines Kreisels, die durch eine äußere Kraft bedingt wird. In diesem Falle jedoch, kommt der Effekt von der einfachen Bewegung im freien Fall entlang einer Bahn, die so gerade wie möglich durch die Raumzeit verläuft – einer Geodäte. Ein anderer Name ist die de Sitter Präzession, benannt nach dem niederländischen Astronom Willem de Sitter, der 1917 als Erster diese Konsequenz der Allgemeinen Relativitätstheorie hergeleitet hat.

Die Umlaufbahn in unserem Beispiel ist ähnlich der von Gravity Probe B, einem Satelliten, der 2004 ins All geschossen wurde um nicht nur die Auswirkungen der geodätischen Präzession zu messen, sondern auch einen Effekt, der Frame-Dragging genannt wird – einer Verschiebung, die in der Nähe von sich drehenden Massen auftritt.  Um dies zu tun überwacht Gravity Probe B die Ausrichtung seines internen Kreisels relativ zu einem weit entfernten Bezugsstern – nicht nur an einem Punkt des Orbits, sondern kontinuierlich um auch Effekte, wie die relativistische Lichtablenkung, die die Richtung des Sternenlichtes ändert, während der Satellit sich entlang seiner Umlaufbahn bewegt, zu berücksichtigen.

Bis jetzt wurde geodätische Präzession hauptsächlich mithilfe von natürlichen Satelliten gemessen. So ist es möglich das Erde-Mond-System als gigantischen Kreisel anzusehen, dessen Drehachse durch die Bewegung des Mondes um die Erde definiert wird. Durch die Beobachtung dieses Systems war es möglich, die Vorhersagen der Allgemeinen Relativitätstheorie bis auf eine Genauigkeit von wenigen Prozent zu testen.

In jüngerer Zeit wurde die geodätische Präzession in Doppelpulsarsystemen beobachtet, in denen zwei superdichte Neutronensterne einander umkreisen. In der Nähe von solchen sehr kompakten Objekten ist die Krümmung so ausgeprägt, dass die Richtungsverschiebungen bis zu einem Grad pro Jahr betragen können!

Weitere Informationen