From force to field

About fields – a central concept that is relevant not only for gravitational physics

An article by Markus Pössel

The description of forces acting at a distance – e.g., the electrostatic force, by which a particle with electric charge can influence other charged particles – usually involves at least two particles acting on each other, never just one. This isn’t without reason, because in general the strength of such a force between two particles A and B is proportional to the charge of particle A as well as to the charge of particle B. Therefore, without knowing the charges of both particles, the strength of the force cannot be determined at all.

Nevertheless, in many situations, it is meaningful and useful to describe the influence of charged particles without immediately bringing a concrete target object of this influence into play. The physical quantities suitable for this are called force fields or, somewhat more general, shorter and far more usual, fields.

From sign to arrow

Let us consider the simplest case, the electric field around a charged metal sphere, which belongs to the electrostatic force. Figuratively, we can think of it as if at every point in space around the metal sphere, a small sign like the following would be floating:

Field sign cautioning the reader that a particle with an electric charge of 1 Coulomb would experience a force of 2.629 Newton to the right.

If you want to find out the force on a particle which is at a certain place, you just have to read the imaginary sign at this place. It indicates the force exerted by our metal sphere on a reference particle with an electric charge of 1 Coulomb. If the particle we are concerned with has a larger or smaller electric charge than 1 Coulomb, the acting force will accordingly be larger or smaller. Specifically, if our particle has a charge of X coulombs, then the force acting on it is X times the force on the reference particle noted on the plate.

Another convention takes into account that positively and negatively charged particles feel opposite electrical forces in the same situation: where a positively charged particle is repelled, a negatively charged one is attracted. Our reference particle is positively charged by definition, and therefore the following applies: If the charge of the particle we consider (and thus the factor X) is negative, then a force acts on this particle exactly opposite to the direction of the arrow of the sign.

Of course, it is unnecessary to repeat the information which is the same on every sign – that the statement applies to a particle of the charge 1 Coulomb and that the quantity stated is a force. What really matters are only two pieces of information that must be known at each location: The strength and the direction of the force on the reference particle. No actual sign is needed for these two pieces of information, a simple arrow is sufficient, in the language of mathematicians a “vector”:

Here, the length of the arrow indicates the strength of the force experienced by the test particle located at the base point P, and its direction indicates the direction of action of the force. Here is an example:

A vector shows strength and direction of a force on a reference particle

Comparing the length of the arrow with the specified length scale that should apply to our arrows – a distance that should correspond to one thousandth of one Newton, or millinewton, mN, as the length of the arrow – shows that a force of 2 millinewtons acts on a reference particle at the drawn location P in the direction of the arrow.

A crowd of arrows

Strictly speaking, one such field vector is defined for each point in space. The totality of all these arrows form the electric field. In a visual representation, of course, one will actually draw only very few of these vectors – just enough so that the individual vectors can be recognized, and that the totality of vectors gives a good overview of the properties of the field in question. Here are some representative arrows that give us an overview of the electric field around a charged metal sphere that carries a charge of 2 Coulombs and has a diameter of 16 centimeters:

Electric field around a charged sphere

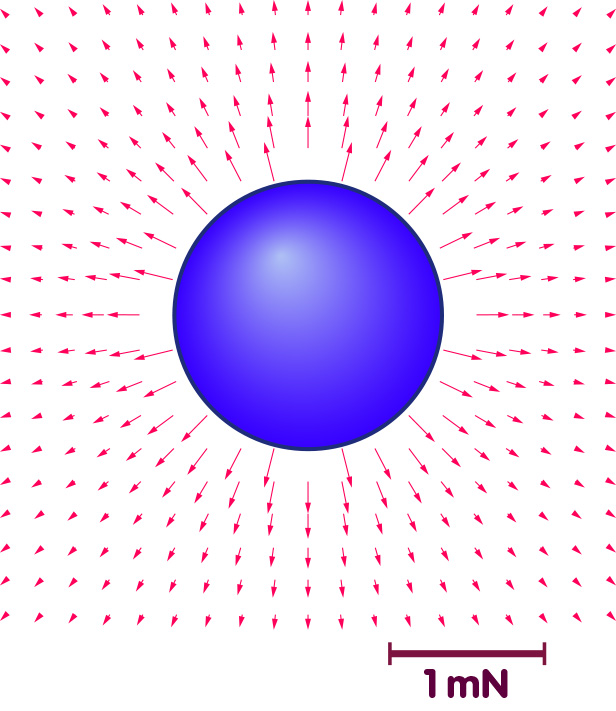
Clearly indicated by the vector arrows: The force is directed directly away from the center of the sphere at each location. This is not unexpected: The positively charged sphere electrically repels our positive reference particle. The further we move away from the center of the sphere, the shorter the arrows become. This is no surprise either: the electrical force between two charges is smaller the further apart the charges are. By precisely measuring the lengths of the arrows, one can also read from the figure how the strength of the force depends on the distance: it is inversely quadratic, i.e. at double distance, the force is only a quarter as strong as before.

The gravitational field

In analogy to the electric field, the field belonging to Newton’s gravitational force can be defined as well: Each arrow indicates the force acting on a reference particle with a mass of one kilogram. In one respect the situation is even simpler than with the electric force: There is only one kind of mass, and all masses attract each other. The arrows – the field vectors – therefore directly indicate the direction of the force in each case, without having to worry about positive and negative charges.

In the following figure selected field vectors around a spherical central mass like the earth are shown:

Gravitational field around the spherical mass of the Earth

All field vectors point directly to the center of the Earth – this is where the gravitational force of the globe is directed, acting on all particles in the vicinity of our planet. The strength of the gravitational force – the length of the arrows – decreases with the square of the distance.

Magnetic fields

For the electric field and the Newtonian gravitational field, the field vectors are directly aligned with the force acting on the reference particle. For magnetic fields, the relationship is somewhat more indirect, but again, the following applies: the force exerted by a magnet on passing electrically charged particles is associated with a field that assigns a magnetic field vector to each point in space. As an example, the following figure shows the magnetic field vectors of a simple bar magnet with north and south poles:

Magnetic field of a bar magnet

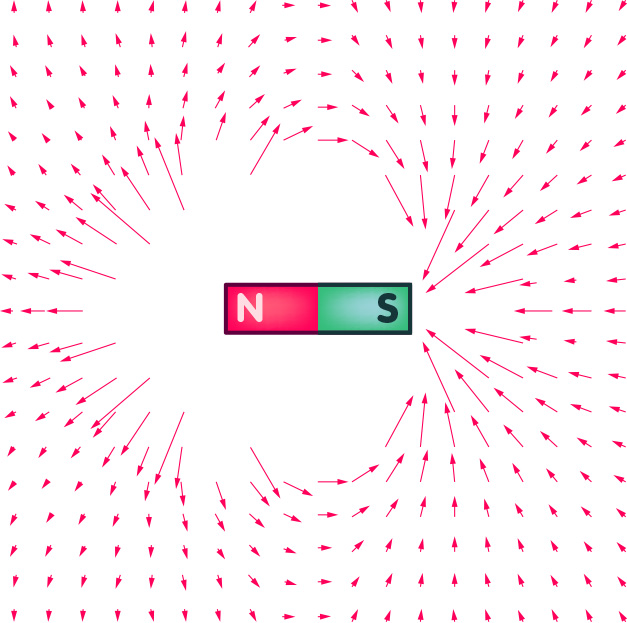
Only vectors starting at a certain minimum distance from the magnet are shown. Vectors whose base points are further inside would be so long that they would intersect the outer vectors and make the figure unclear.

One meaning of the magnetic field vectors is easy to understand: If a small magnet is put into the existing magnetic field, then forces act trying to rotate the small magnet so that its orientation is exactly parallel to the magnetic field arrow (with the north pole in the direction of the arrow):

Kompassnadel im Magnetfeld

This effect has a highly practical application: it ensures that a freely rotating compass needle points north.

More generally, magnetic fields are accompanied by a force on moving electric charges. However, it does not act directly in the direction of the field arrow, but somewhat differently: the speed of a particle can also be assigned an arrow – the length of the arrow indicates how fast the particle is moving, the direction of the arrow indicates in which direction it is flying. The direction of the deflecting force is derived from the so-called right-hand rule: spread the thumb, index finger and middle finger of your right hand so that two of the fingers are perpendicular to each other – the thumb extended, the index finger straight and the middle finger at right angles to the palm. Let’s assume that your thumb points in the direction of the magnetic field vector, and your middle finger points in the direction of the velocity of an electrically charged particle in this magnetic field – more precisely: in the direction of that part of the velocity which corresponds to a movement perpendicular to the magnetic field vector. Then the particle experiences a force in the direction of your index finger, as sketched in the following figure:

Three fingers of one's right hand can be associated with the directions of the magnetic field, which is perpendicular to the velocity, which is perpendicular to the force.

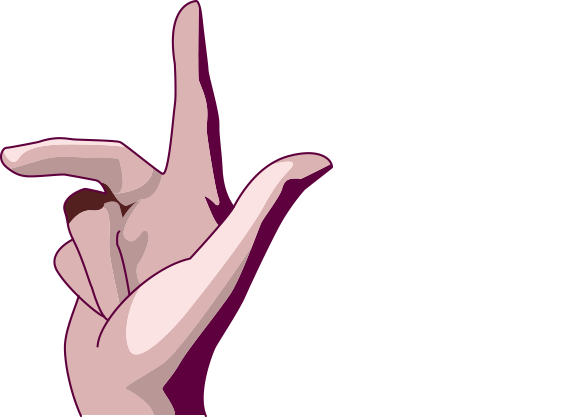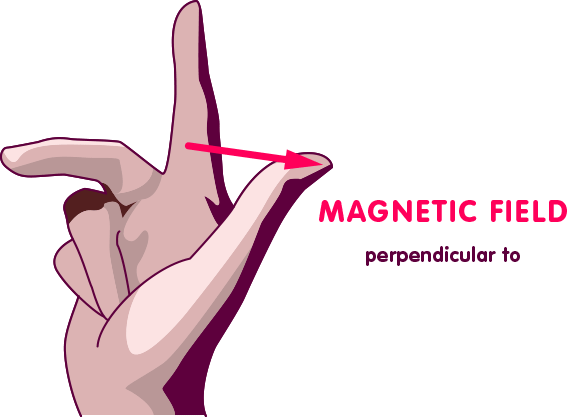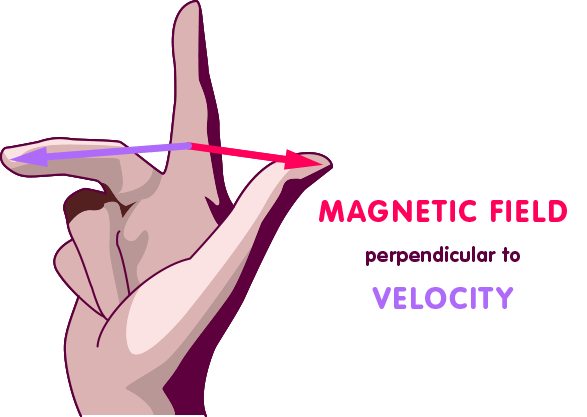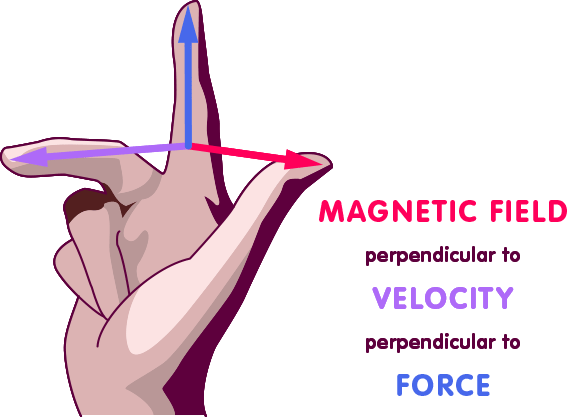
The magnitude of the force is the product of the velocity, the strength of the magnetic field, and the electric charge of the particle.

For a more general direction of motion of the particle, one uses the just mentioned mnemonic by considering only that part of the particle speed that is perpendicular to the magnetic field, in order to get from the field to the force.

The dance of fields and particles

After the previous descriptions it may seem as if force fields are only an auxiliary construction to describe distant forces between matter particles. In fact, however, there are good reasons to regard particles and fields as equally real. Let us take the electromagnetic field as an example: Just like particles, electric and magnetic fields also have an energy – a region of space in which the electric or magnetic field deviates from zero contains corresponding energy. In addition, electromagnetic fields do not only occur rigidly bound to electrically charged objects or magnets as in the picture examples shown above. Under suitable circumstances, field configurations occur which, following the basic equations of electromagnetism, propagate through space almost completely independently: These are electromagnetic waves such as light.

Therefore, the events in a region of the universe filled with electrically charged particles result, from today’s point of view, from the interaction of fields and particles: Where the charged particles are located and how they move determines the properties of the electric and magnetic fields that fill space. The electric and magnetic fields, in turn, affect particle motion: As discussed in the definition of electric and magnetic fields above, electric fields result in a force on charged particles, magnetic fields result in a force on moving charged particles. The changed positions and the changed motion of the particles lead to corresponding changes of the fields, which in turn influence the particle motion thereupon somewhat differently, and so on and on in an endless dance of fields and particles.

Whoever wishes to describe the evolution of such a particle-field ensemble must describe this dance, in which particles and fields mutually influence each other.

To put it more mathematically, the following applies: The electric and magnetic fields that result for a given charge configuration are determined by the so-called field equations. How the particle motion is influenced by the fields is governed by the so-called equations of motion. If you want to describe the evolution of a particle-field ensemble, you have to solve the coupled system of equations consisting of both field equations and the equations of motion.

Not only for vectors

In the above examples for fields, each point in space was associated with a field vector – a quantity with direction and length. More precisely, even each point in space at each instant can be assigned a field vector, since fields can change over time, as explained in the last section.

In general, we are dealing with a field whenever a value of a certain physical quantity is assigned to every point in space at every point in time. This need not be a vector, but may well be other types of quantities. In certain situations, such as describing a star, it may be useful to assign a temperature value to each region of space, indicating the temperature of the stellar gas it contains. This is not a vector, but a simple numerical value.

On the other hand, there are more complicated possibilities: In general relativity, a quantity defined at each point, called “metric field” or, in short, “metric”, describes the geometry of the space region in question at the given time. This quantity thus contains all the information needed to describe how the geometry of the corresponding spacetime is distorted. In general relativity, the distortion is directly related to gravity, and in this sense the metric is something like the gravitational field of the theory.

Further Information

This section introduces the notion of field, which is fundamental in both special and general relativity (and not only there). Basic information on the fundamentals of both theories is provided in the chapters Special Relativity and General Relativity in Elementary Einstein.

Colophon

Markus Pössel

is the managing scientist at Haus der Astronomie, the Center for Astronomy Education and Outreach in Heidelberg, and senior outreach scientist at the Max Planck Institute for Astronomy. He initiated Einstein Online.

Citation

Cite this article as:
Markus Pössel, “From force to field” in: Einstein Online Band 13 (2021), 1007

Definitioner

Newton

Englischer Physiker (1643-1727), siehe weiter unten Newtonsche Gravitation. Die Einheit der Kraft im internationalen Einheitensystem (SI). Ein Newton entspricht dabei der Kraft, die nötig ist, um einem Objekt mit einer Masse von einem Kilogramm eine Beschleunigung von einem Meter pro Sekunde-Quadrat zu erteilen.

velocity

In physics, velocity is a combination of two aspects: First of all, how fast an object is, in other words: how long a distance it moves in a given time (its "speed"). Secondly, the direction in which an object moves. Physicists combine these two informations into a single mathematical object, called a "vector", and this is what is called the velocity. For instance, when a car goes around a curve with 100 miles per hour, its speed is constant, but as it changes its direction of movement, its velocity changes correspondingly.

time

It is a fact of life that not all events in our universe happen concurrently - instead, there is a certain order. Defining a time coordinate or defining time, the way physicists do it, is to define a prescription to associate with each event a number so as to reflect that order - if event B happens after event A, then the number associated with B should be larger than that associated with A. The first step of this definition is to construct a clock: Choose a simple process that repeats regularly. (What is "regular"? Luckily, in our universe, all elementary processes such as a swinging pendulum, the oscillations of atoms or of electronic circuits lead to the same concept of regularity.) As a second step, install a counter: A mechanism that, with every repetition of the chosen process, raises the count by one. With this definition, one can at least assign a time (the numerical value of the counter) to events happening at location of the clock. For events at different locations, an additional definition is necessary: One needs to define simultaneity. After all, the statement that some far-away event A happens at 12 o'clock is the same as saying that event A and "our clock counter shows 12:00:00" are simultaneous. The how and why of defining simultaneity - a centre-piece of Einstein's special theory of relativity - are described in the spotlight topic Defining "now". With all these preparations, physicists can, in principle, assign a time coordinate value ("a time") to any possible events, and describes how fast or how slow processes happen, compared to that time coordinate.

temperature

In systems consisting of many particles, be they solid bodies, fluids or gases, the constitutents are in constant, chaotic motion: the atoms in a solid crystal oscillate a bit, the molecules of a gas are in rapid, disordered motion, and so on. The average energy with which each constitutent contributes to every part of the disorderly motion is the same, and it is called the temperature of the system. High average energy corresponds to high temperature - atoms vibrating wildly, gas molecules zipping around very fast -, low average energy to low temperature. In a slightly different context, certain mixtures of electromagnetic radiation can be assigned a temperature ("radiation temperature"), a single parameter that completely defines the basic properties of the radiation (more precisely, its spectrum). It corresponds to the thermal radiation emitted by a hot body with precisely that temperature. In physics, temperature is measured in Kelvin, in everyday life, depending on the country, in Fahrenheit or Celsius.

sphere

A spherical surface is a simple example for a curved surface. It is easily pictured as a surface embedded in three-dimensional space: a spherical surface is the set of all points at a certain fixed distance from a given point (the point being the centre of the sphere). Mathematically, a spherical surface can be described without recourse to three-dimensional space - when mathematicians talk of the geometry of such a surface, they (almost) always mean the "inner geometry": Those properties of the surface noticeable to two-dimensional beings, living and working in that surface, capable of measuring distances and angles in it. Sphere is regularly used as a synonym for spherical surface (instead of describing a solid, three-dimensional ball). And not only for the two-dimensional spherical surface described above, but also for its analogues in lower and higher dimensions. A one-sphere, for instance, is the same as a circle, a two-sphere is the spherical surface defined above, a three-sphere its three-dimensional analogue.

speed

An object's average speed is the distance it moves during a given period of time, divided by the length of the time interval. If you make the time interval infinitely small, the result is the object's speed at one particular moment in time. The notion of speed can be applied to waves in different ways; for instance, for a simple wave, the phase speed is the speed at which any given wave crest or wave propagates through space. See also the more general entry velocity.

space

In a strict sense: Space as we know it from everyday life: the totality of all locations in which objects can sit, with three dimensions. In a more general sense used by mathematicians, all kinds of sets of points are spaces - a line for instance, which has but a single dimension, or a two-dimensional surface, but also higher-dimensional spaces. Also, in such more general spaces, geometry can be different from the standard Euclidean geometry taught in high schools - such spaces can be curved.

point

Elementary "building block" of geometrical entities such as surfaces or more general spaces. For instance, a surface is the set of all its points, of all possible locations on the surface, and all geometrical objects in that surface are defined by the points that belong to them - for instance, a line on the surface is the set of (infinitely many) points.

planet

Planets are not-too-small companions of a star that are not stars themselves (nor ever were stars). In our solar system, the planets are, listed from the one closest to the sun to the one farthest: Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune. As of August 2006, Pluto, which used to be a proper planet, is officially a "dwarf planet". In the night sky, the distinguishing characteristic of planets is that they move around relative to the unchanging background of stars - which gave them their name, loosely translated from Greek as "wanderers".

Newton

English physicist of the 16th/17th century, see Newtonian gravity, below.

In the international system of units (SI) the unit of force, abbreviation N. One Newton is the force needed to impart on a body of mass one kilogram an acceleration of one metre per second-squared.

matter

In general relativity: All contents of spacetime that contribute to its curvature: particles, dust, gases, fluids, electromagnetic and other fields. In particle physics: All elementary particles with half-integer spin, such as electrons and quarks, as well as their composites such as protons and neutrons, in contrast with force particles.

mass

In classical physics, mass plays a triple role. First of all, it is a measure for how easy it is to influence the motion of a body. Imagine that you're drifting in emtpy space. Drifting by are an elephant and a mouse, and you give each of them a push of equal strength. The fact that the mouse abruptly changes its path, while the elephant's course is as good as unaltered, is a sure sign that the mass (or, in the language of physics, the inertia or inertial mass) of the elephant is much greater than that of the mouse. Secondly, mass is a measure of how many atoms there are in a body, and of what type they are. All atoms of one and the same type have the same mass, and adding up all those tiny component masses, the total mass of the body results. Thirdly, in Newton's theory of gravity, mass determines how strongly a body attracts other bodies via the gravitational force, and how strongly these bodies attract it (in this sense, mass is the charge associated with the gravitational force). In special relativity, one can also define a mass that is a measure for a bodies resistance to changing its motion. However, the value of this relativistic mass depends on the relative motion of the body and the observer. The relativistic mass is the "m" in Einstein's famous E=mc² (cf. equivalence of mass and energy). The relativistic mass has a minimum for an observer that is at rest relative to the body in question. This value is the so-called rest mass of the body, and when particle physicists talk of mass, this is usually what they mean. Just as in classical physics, the rest mass is a kind of measure for how much matter the body is made up of - with one caveat: For composite bodies, the energies associated with the forces holding the body together contribute to the total mass, as well (another consequence of the equivalence of mass and energy). In general relativity, mass still plays a role as a source of gravity; however, it has been joined by physical quantities such as energy, momentum and pressure.

magnetic field

The magnetic force is a force by which electric currents (i.e. moving electric charges) act on each other; the magnetic field is the associated field. All phenomena related to the magnetic force or magnetic field are subsumed under the heading of magnetism. Magnetic fields cannot be understood separate from electric fields - their complete description is possible only within the more general context of electromagnetism.

light

Light in the strict sense of the word is electromagnetic radiation the human eye can detect, with wave-lengths between 400 and 700 nano metres. In relativity theory and in astronomy, the word is often used in a more general sense, encompassing all kinds of electromagnetic radiation. For instance, astronomers might talk about "infrared light" or "gamma light"; in this context, light in the stricter sense is referred to as "visible light". Within classical physics, the properties of light are governed by Maxwell's equations; in quantum physics, it turns out that light is a stream of energy packets called light quanta or photons. In the context of relativistic physics, light is of great interest, and for a number of reasons. First of all, the speed of light plays a central role in both special and general relativity. Also, there are a number of interesting effects in general relativity which are associated with the propagation of light, namely deflection, the Shapiro effect and the gravitational redshift.

lead

Chemical element with the symbol Pb; each lead nucleus contains 82 protons. Lead nuclei, stripped of their electrons, are among the types of heavy ions which are brought into collision in particle accelerators such as the Relativistic Heavy Ion Collider in order to recreate the state of matter in the early universe shortly after the big bang.

kilogram

In the international system of units (SI), the unit of mass; until May 2019 defined by a reference mass that is kept in Paris, France. From then on by definition of the Planck constant and of the Avogadro number that has an exact experimental value used for the definition of the Mol.

interaction

Interactions are all the different ways in which elementary or compound particles can influence each other. In elementary particle physics, "interaction" and "force" are used synonymously.

In the standard model of elementary particles, there are three fundamental interactions: electromagnetism, the strong nuclear force and the weak nuclear force. For another interaction, gravity, there is no quantum description yet.

gravity

See gravitation

gravitational field

The totality of all gravitational influences that one or more massive objects can exert on bodies in their vicinity.

More precisely: At every location in space, the gravitational field is defined as the acceleration that a small test particle present at that location would feel due to the gravitational forces of the masses around it.

gravity (gravitation)

In classical physics: An action-at-a-distance force by which all bodies that possess mass attract each other (see Newtonian theory of gravity), synonym: gravitational force. In Einstein's general theory of relativity: The fact that matter that possesses mass, energy, pressure or similar properties distorts spacetime, and that this distortion in turn influences whatever matter might be present. An introduction to the basic ideas of general relativity is provided by the section General relativity of Elementary Einstein. More information about the nature of gravity in general relativity can be found in the spotlight text Gravity: From weightlessness to curvature.

general relativity (general theory of relativity)

Albert Einstein's theory of gravity; a generalization of his special theory of relativity. For information about the concepts and applications of this theory, we recommend the chapter general relativity of our introductory section Elementary Einstein. Further information about many different aspects of general relativity and its applications can be found in our section Spotlights on relativity.

gas

In a strict sense: A state of matter in which the atoms and/or molecules wildly careen and collide, without being bound to each other. This movement leads to an inner pressure, while the average kinetic energy of the moving particles is a measure for the temperature of the gas. Compare the other states of matter: solid state, liquid, plasma. In a broader sense, gas is also used to denote other mixtures of freely careening particles, for instance in the case of the electron gas whose pressure stabilizes a white dwarf against further collapse.

force

In mechanics: Influence acting on a body, trying to accelerate it.

More generally: All influences by which elementary or other particles can interact; in this sense, force and interaction are synonymous. In the standard model of particle physics, there are three elementary forces: electromagnetism, the weak (nuclear) force and the strong (nuclear) force, while there is no quantum description of the fourth fundamental interaction, gravity.

field

A field describes how a physical quantity is distributed in space and time. For instance, the area where electric forces act on a test particle is subject to an electric field. Or the gravitational forces which act on the mass of a test body define a gravitational field. In general a field contains energy, occupies space and can change over time.

energy

Physical quantity with the special property that, in physical processes, energy is neither destroyed nor created, simply transformed from one form of energy to another. Some of the different forms of energy that are defined separately are kinetic energy, thermal energy and the energy carried by electromagnetic radiation. Processes that transform one form of energy into another take place in all machines we use in everyday life, from the engine of a subway train (electrical energy into kinetic energy of the train) to an electric blanket (electrical energy into thermal energy). One important consequence of special relativity is that energy and mass are completely equivalent - two different ways to define what is, on closer inspection, one and the same physical quantity. See the keyword equivalence between mass and energy.

electrostatic force

An action-at-a-distance-force that acts between electrically charged bodies merely because of the fact they carry electric charge.

electromagnetism

Electromagnetism is the totality of all phenomena associated with the presence of electric charges, such as the electric force, magnetic force or electromagnetic waves. The basic laws of electromagnetism are Maxwell's equations. In the context of special relativity it becomes clear that electric and magnetic forces are relative - which one of them is active in a given situation depends on the observer. Say that, from the point of view of one observer, the attractive force between an electric conductor and a moving charged particle is purely electric in nature - nevertheless, for a moving observer at rest with respect to that particle, it is purely magnetic. Just as, in special relativity, it makes sense to talk of spacetime as a whole, seeing that it depends on the observer how that spacetime is then split into space and time, it makes sense to talk collectively about "the electromagnetic force", leaving it to the different observers to split this electromagnetic force into electric or magnetic parts.

electric field

The electric force is a force by which electric charges act on each other; the electric field is the associated field.

Electric fields cannot be understood separate from magnetic fields - their complete description is only possible within the more general context of electromagnetism.

In the simplest case, namely in situations that do not change over time, the electric force is the so-called electrostatic force.

electric force (electric field)

The electric force is a force by which electric charges act on each other; the electric field is the associated field.

Electric fields cannot be understood separate from magnetic fields - their complete description is only possible within the more general context of electromagnetism.

In the simplest case, namely in situations that do not change over time, the electric force is the so-called electrostatic force.

electric charge

The charge associated with electromagnetism: a property of objects that determines the strength of the electric force with which they act on other charged objects, and the strength of electric forces by which other such objects act on them. Moving electric charges produce a magnetic field, and are influenced by such fields.

Earth

Our very own planet in the solar system - the third planet from the sun. The earth has a mass of about 6 trillion trillion (in exponential notation, 6·10²⁴) kilograms.

charge

A measure of the strength of a force (action-at-a-distance) originating from a body, and of how susceptible it is to being influenced by other bodies via the same force. The most famous example is electric charge: Electrically charged bodies act on other electrically charged bodies via an electric force whose strength is proportional to the electric charges of the bodies involved. It is a characteristic property of charges that they are conserved; they can neither be created from nothing nor simply disappear. For instance, when a positron with electric charge +1 (in suitable units) and an electron with electric charge -1 annihilate to give electromagnetic radiation, overall charge conservation is satisfied: Before the annihilation, the sum of the electric charges was 1+(-1)=0, and afterwards, when there is only uncharged electromagnetic radiation left, it is also zero. In the context of particle physics, there are more abstract charges not directly connected with forces and interaction, but subject to similar conservation laws.