Time determination with radio signals – from radio-controlled clocks to satellite navigation

How to determine the exact time anytime and anywhere with the help of a radio receiver (and some additional information)

An article by Markus Pössel

Conventional radio-controlled clocks in Germany have a receiver for the time signal of the long-wave transmitter DCF77 in Mainflingen near Frankfurt am Main, which is controlled by the Physikalisch-Technische Bundesanstalt. This is a clock signal – a radio signal whose strength (more precisely, whose amplitude) periodically decreases to show that a new second has begun, as outlined here:

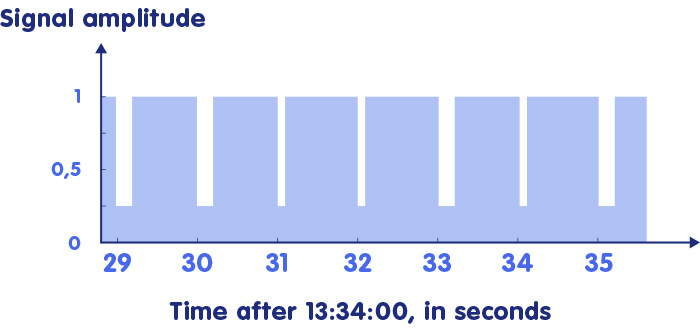
The beginning of the drop represents the second beat. But the signal contains more information. As shown in the figure above, there are shorter and longer sinking intervals (one or two tenths of a second long). Similar to the sequence of zeros and ones in the binary code of a computer or the dot-dash sequence of a message in Morse code, this sequence of shorter and longer pulses in the course of a minute contains, among other things, the minute in which the radio station sent out the time signal in question (the radio clock must then count for itself which second in this minute it is – it recognizes the start of a new minute by the fact that the drop in signal strength stops at the fifty-ninth second). In the above example, the sequence long-long-short-short-long-short-long just indicates that the time signal refers to hour 13. The radio-controlled clock can therefore always display the correct time without having to be adjusted by hand. Switching to summer and winter time is also automatic.

Radio-controlled clocks and the question of simultaneity

But is the display of the radio-controlled clock really completely accurate? Anyone who has the basics of special relativity in mind, especially Einstein’s definition of simultaneity, will quickly come up with the answer: No, without assistance, the radio-controlled clock always lags a little. For example, if I set up my radio-controlled clock 300 kilometers away from Mainflingen, it will receive the time signal representing the time 12:00:00,000 only one thousandth of a second later, i.e. at 12:00:00,001. The reason: the radio signal, which travels at the usual speed of light of around 300,000 kilometers per second, takes one thousandth of a second to travel from the transmitter to the receiver. While my watch shows 12:00:00,000 according to the signal just received, in reality it is already 12:00:00,001. Admittedly, such an exact time measurement is rarely needed in everyday life. But here it should be about the principle.

For clocks at a fixed, known location, the solution is simple. If we know where we are, and if we also know that the radio signal needs the time Δt to reach us, then it is sufficient to advance the display of our radio clock constantly by Δt, and the clock will henceforth show the correct time. In the above example: If we program our radio clock to always display the time Δt when a certain time signal t is received, where Δt is equal to one thousandth of a second, then: when the time signal 12:00:00,000 is received, our radio clock will display 12:00:00,001, which is the correct time, given the radio signal’s propagation time.

Radio receivers on the road

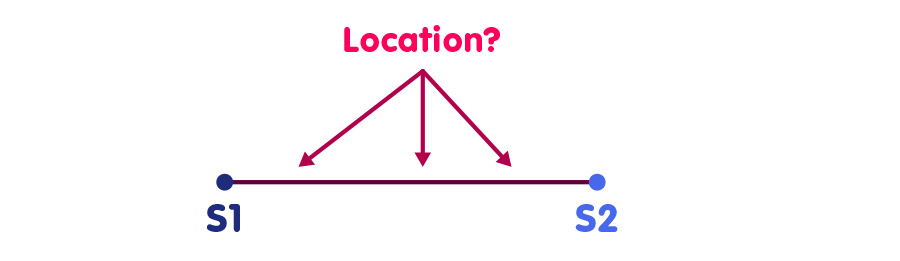
Things get a bit more difficult if we want to take our clock with us on a trip, without knowing exactly where we are at a certain time. However, this can also be remedied. For the sake of simplicity, imagine that you already know that you are on the connecting line between two radio transmitters S1 and S2, each of which transmits a time signal:

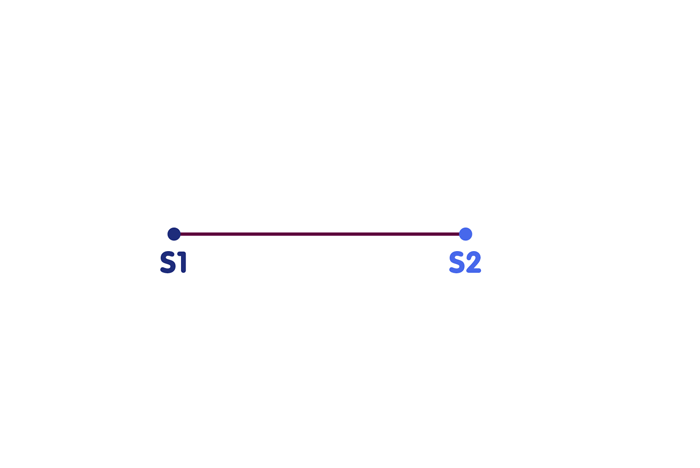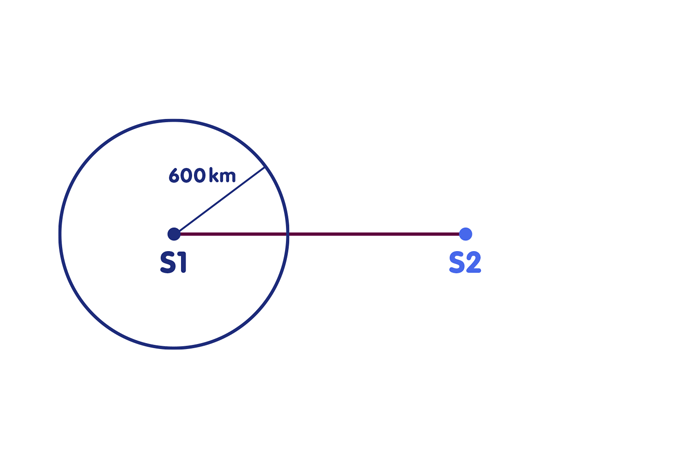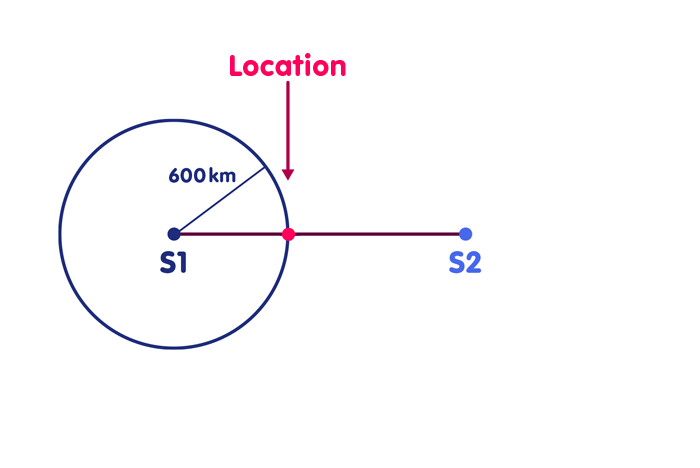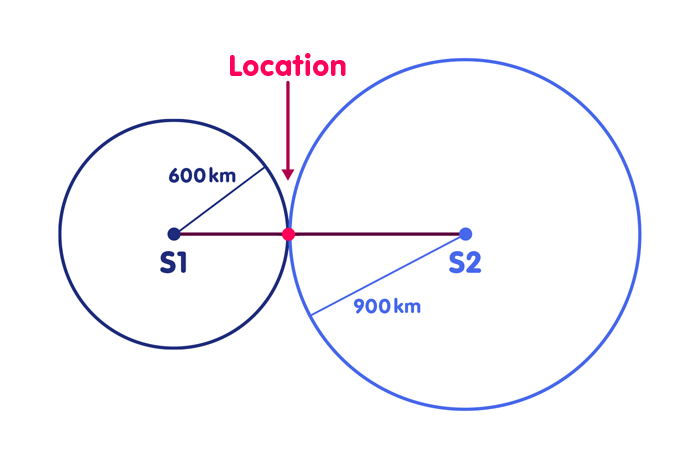
Scenario 1: You already have a perfect clock synchronized with the reference clocks of the radio stations. Then already the reception of a single time signal is sufficient to determine your position on the straight line, at least if each time signal carries the information when and where it was sent. For if the time signal of transmitter S1, which was sent at 10:45:00.000, arrives at you at 10:45:00.002 – you read the time of arrival from your own clock – then the radio signal obviously took two thousandths of a second to reach you. In this time a light or also a radio signal covers 600 kilometers. You are therefore 600 kilometers away from radio station S1. Draw a circle on the map around the location of S1, the radius of which corresponds to 600 kilometers. Your position is at the intersection of this circle with the line connecting the radio transmitters. Of course, you can do the same with the other radio station S2 – in my example, you are 900 kilometers away from the second station, as shown in the following figure. Of course, the corresponding circle (shown here only in part) around the second radio station must intersect the connecting straight line at the same place, just at your location:

Scenario 2: The same location conditions, but now you only have one clock, which is not very accurate. Let’s assume that compared to the atomic clocks at the location of the radio stations, your clock would be ahead by one thousandth of a second. However, you do not know this, but continue to use the display of your clock to determine your location. Then the following happens. A certain time signal is sent from S1 at 13:00:00,000. It reaches you two thousandths of a second later, at 13:00:00,002. However, your clock is now, as said, one thousandth of a second ahead, so it shows 13:00:003 o’clock when the signal arrives. From the comparison of the information contained in the time signal to the transmission time of the signal and that arrival time, which you read on your clock, you come therefore to the false conclusion, that the signal needed 3 thousandths of seconds to reach you and the radio station S1 is therefore 900 kilometers far away. The fact that your clock is one thousandth of a second ahead let you overestimate the distance to the radio station by 300 kilometers – thus just by the distance which light covers in this thousandth of a second. By exactly this distance you would also overestimate all other distances to radio stations. If a signal of the second radio station S2 is sent at 13:00:00,000 o’clock and gets to you at 13:00:00,003, you will read on your clock the wrong arrival time 13:00:00,004 o’clock and infer that the signal travelled 4 thousandths of a second and S2 must therefore be 1200 kilometers away. If you now go back to the map and draw circles, you get the following picture:

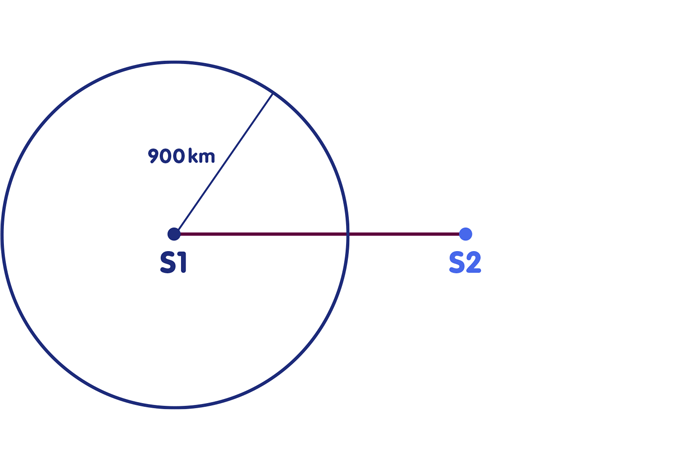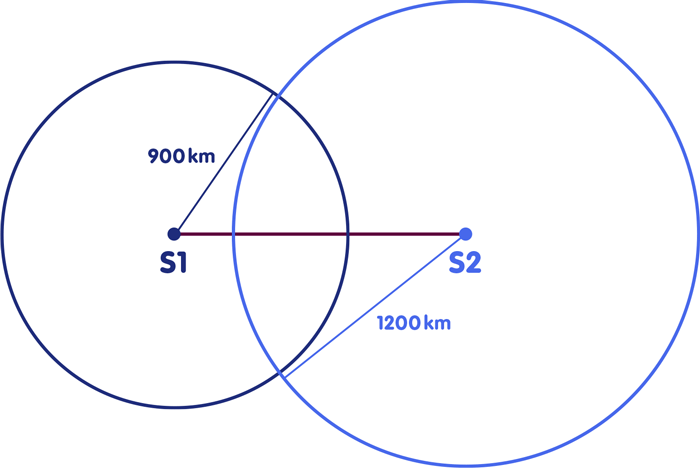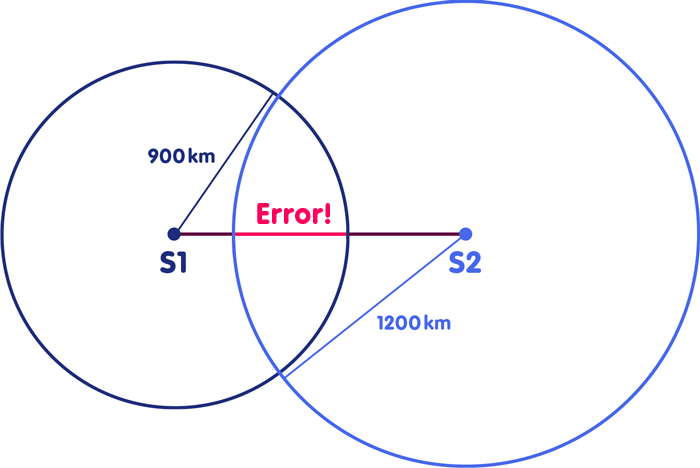
Your clock is ahead, you overestimate all distances and therefore draw circles that are too large and intersect the connecting line in two different points. This is a clear indication that something went wrong, because the circles should actually intersect with the connecting line at a single point, i.e. your position.

Scenario 3 corresponds to Scenario 2, except for the difference that your clock is now not a thousandth of a second ahead, but a thousandth of a second behind. If you use your clock to infer light travel times, the rate error will cause you to underestimate all travel times by one thousandth of a second. You also underestimate all distances by the same distance, 300 kilometers, and this leads to the following wrong picture on the map:

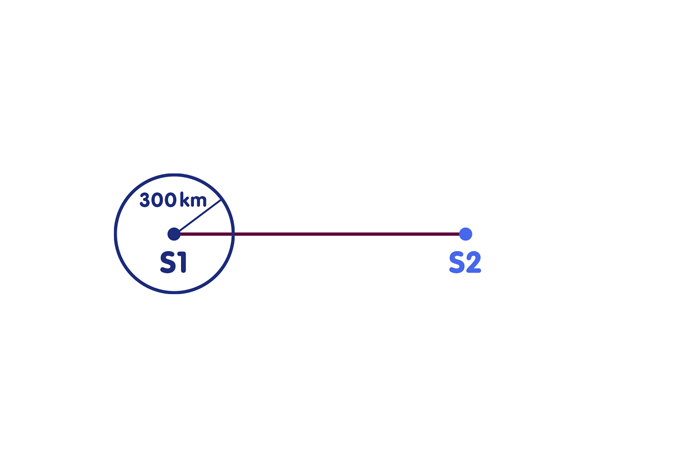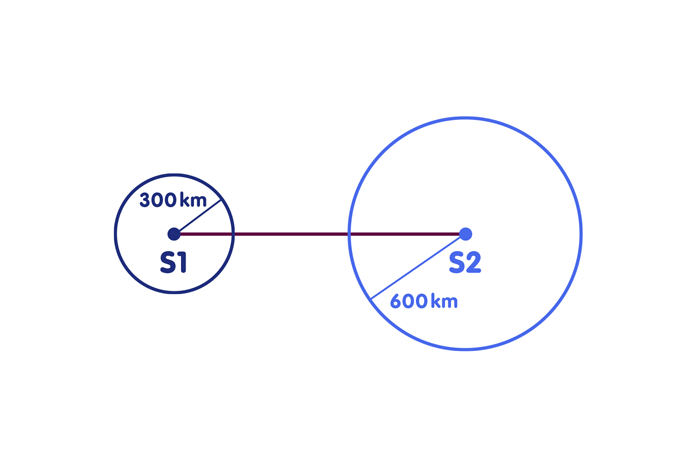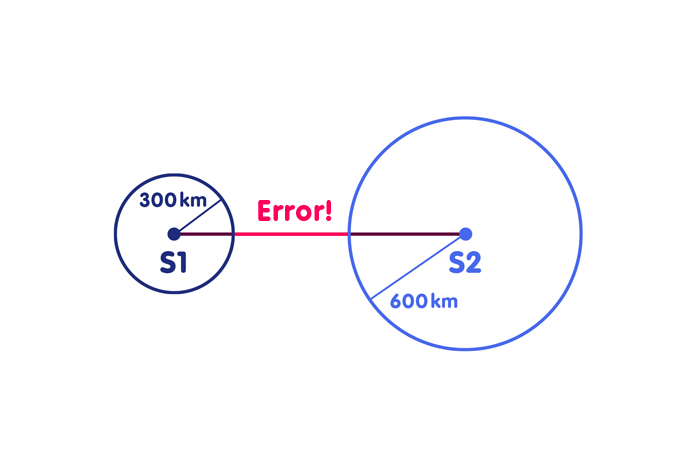
This time both circles have too small a radius. Again it becomes clear that something went wrong, because the circles intersect the connecting line at two different points instead of one.

The crucial step is that the circles not only indicate that something has gone wrong, but directly indicate by which time interval your clock is off. For one thing is characteristic for this situation: all distances are underestimated or overestimated by the same distance. If we see circles on the map, as in the figure above, whose intersections with the connecting straight line do not coincide because the radii are too small, then in our minds we can extend these radii a little by the same distance, so far that the intersections just coincide. The distance by which we had to extend both radii tells us directly by how much our clock is too slow – if we had to extend both radii by 300 kilometers, our clock one thousandth of a second behind, if 600 kilometers extension is necessary, it is two thousandths of a second behind, and so on. In exactly the same way we can shorten the radii of circles which are too large, until the points of intersection coincide, and determine from the necessary shortening, by how much our clock is ahead.

Systematic corrections

Thus, after a necessary excursion into position determination, we are back to our initial problem, that of time determination. Because if we know by how much our clock is ahead or behind the atomic clocks at the location of the two radio clocks, we can compensate the error, and then our clock shows exactly the time of these atomic clocks.

Now we only have to draw a critical consequence from the last two scenarios: The incorrect time display on our clocks did not contribute any information to our time determination. Also for a stopped clock, we could define the correction term “indicated time minus true time” and thus determine the time of arrival of the signals. The given procedure even works if we have no clock available at our location: For two time signals from the two radio stations arriving at us at the same time, we could reconstruct when they arrive at us even without any prior clues. For let us say that the signal of the first station carries the information that it was sent out at 14:30:00,002 o’clock, that of the second station at 14:30:00,001 o’clock. We know that the two stations are 1500 kilometers apart. Suppose that the signals arrive at 14:30:00,003 o’clock. Then the first would have traveled one thousandth of a second, corresponding to 300 kilometers, the second two thousandths of a second, corresponding to 600 kilometers. In total, this adds up to 900 kilometers, much smaller than the radio station distance – so the hypothetical distance circles are much too small, our estimated time is too early. On the other hand, suppose the signals had arrived at 14:30:00.005. Then the first radio station would be 900 kilometers away, the second 1200 kilometers. The sum of the distances would clearly be larger than their true distance of 1500 kilometers – the hypothetical distance circles would be too large, the time we estimated is too late. Thus we have already narrowed down the real time. In fact, it can be determined exactly from the condition that the two distance circles intersect the connecting line in one and the same point – in our simple example even with quite simple mathematics: The calculation is exactly the same as in that notorious school problem where we have to determine at which time two trains, leaving from given stations at given times, meet on the track. If we know the arrival time of the signals, we can of course determine our location – the point where the two distance circles intersect.

Our example was deliberately chosen to be very simple: We already knew that we were on the straight line connecting the two radio stations. Thus, in the scenario where we had a perfect clock, a single time signal, a single distance determination was sufficient to determine our location (the intersection of the distance circle and the connecting straight line). Without a clock, the reception of two time signals was sufficient to determine both the arrival time of the signals and our location from the condition that the circles intersect the connecting straight line at the same point (just our location). But even without knowing that we are on a certain straight line, we could have used radio signals to determine the distances to the radio transmitters and from that both our position and the exact arrival time of the signals. This is how satellite navigation works, such as the Global Positioning System GPS. Instead of stationary transmitting stations, we are dealing with satellites whose orbits (and thus their positions in space) are precisely known. Some details are given in the spotlight topic Relativity and Satellite Navigation; here, we are mainly interested in the fact that these satellites can also be used to determine time, just like in our simple example: If you have a perfect clock, you have to receive signals from three satellites to determine your position on Earth. Owners of an inaccurate clock or no clock at all, can proceed similarly as described above, if they receive the time signals of four suitable satellites: In their imagination, they can draw a spherical surface around each of the four satellites (analogous to the distance circles in the example above). From the requirement that these four spherical surfaces should intersect at a single point in space – precisely the location of the observer – both the time of arrival of the signals and the searched location can be reconstructed.

In this way, satellite navigation systems such as GPS today are the most accurate way to determine time anywhere. This is related to Einstein’s theories in several ways: The basic idea is derived directly from the definition of simultaneity that Einstein introduced with his special theory of relativity. For a precise execution – as explained in the spotlight topic Relativity and Satellite Navigation – effects of both Special and General Relativity have to be taken into account. The method itself is then in turn used to research Einstein’s theory: In order to be able to compare the data of the various gravitational wave detectors worldwide, their temporal evolution is precisely logged – the highly precise time required for this is provided by the satellite navigation system GPS.

Further Information