General relativity / Elementary Tour part 1: Einstein’s geometric gravity
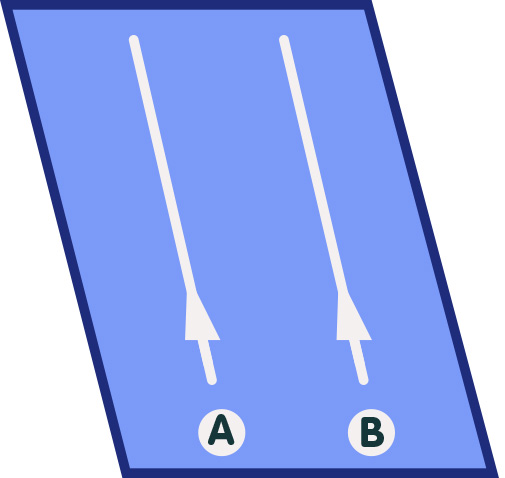
Imagine empty space – in our case, a two-dimensional plane – with no forces acting between the bodies floating around. If there are no forces, then classical mechanics and Einstein’s mechanics of special relativity are in agreement: Under these circumstances, bodies move along the straightest possible lines (which in this case are just straight lines in space) with a constant velocity. In the following image, this is symbolized by the straight paths of two particles A and B:
plane with parallel trajectories
In particular, particles that start to move along parallel trajectories (as in the above image) will never meet, but are fated to remain forever at a constant distance from one another.
In the world of classical physics, if particles diverge from this behavior, it must be because there is a force acting on them. Forces accelerate particles, causing them to leave the straightest possible paths and follow curved trajectories instead. In our two-dimensional example, look at the following picture,
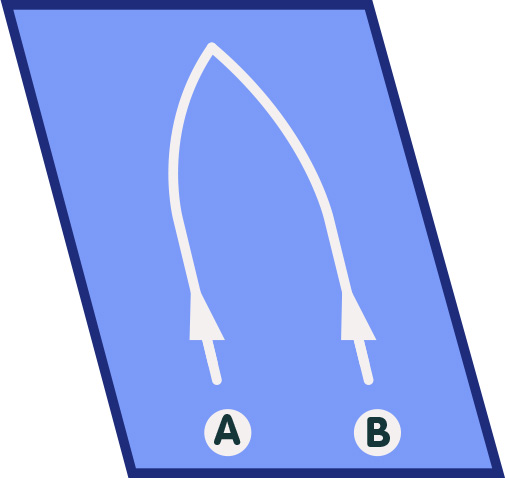
plane with curved trajectories
in which the particles A and B start out in parallel, but are then accelerated towards one another. In Newton’s theory of gravity, gravitation is a force which could cause such an effect. For instance, the reason that the two particles in the above picture accelerate toward each other and then meet could be that they are both attracted gravitationally by a massive body located at the point of their meeting.
However, there is another possibility in which the same situation (where two particles that start out in parallel converge and finally meet) could arise. The two particles could still be moving on the straightest possible lines – not in the plane, but on a curved surface! The following image shows an example:
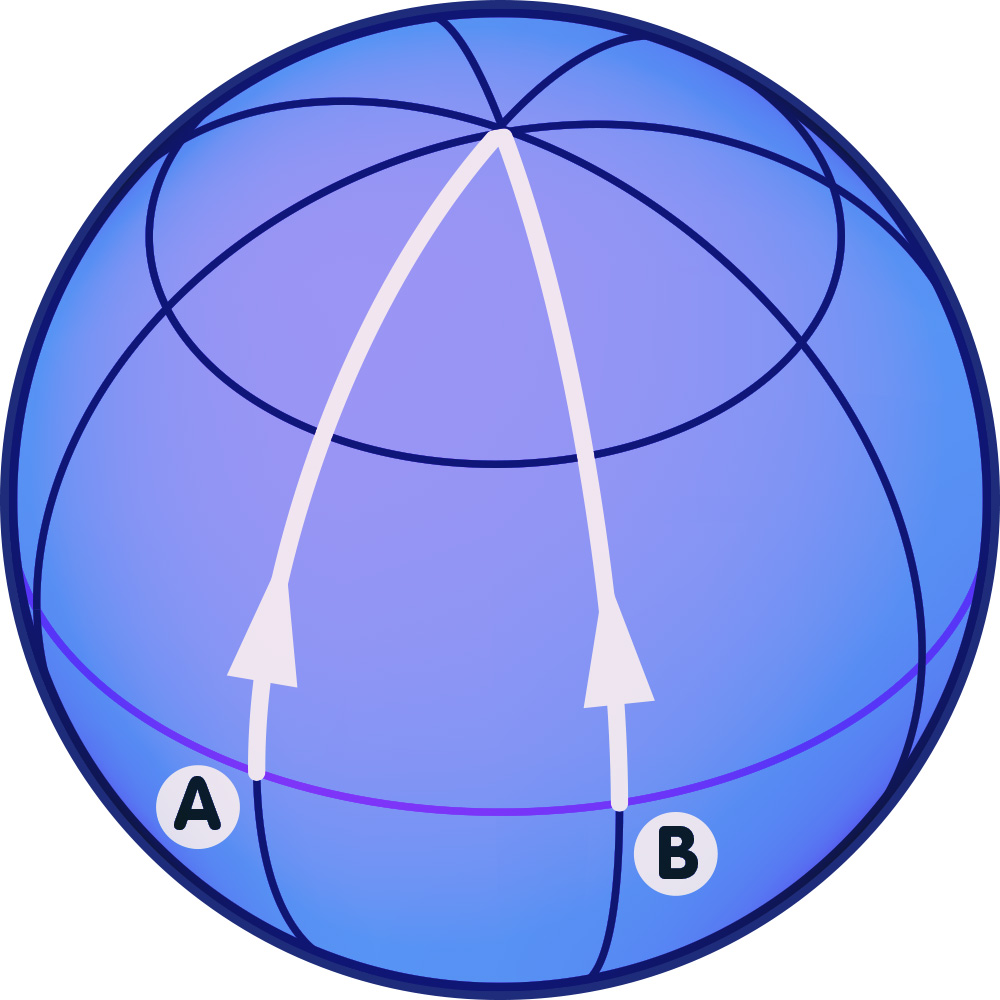
sphere with geodesic triangle
In that situation, there is no force making the particles deviate from the straightest possible lines; the mere fact that the particles are moving on a sphere means that, even if they still move as straight as possible, their paths will converge.
Einstein’s theory is exactly analogous to this. In Newton’s theory, gravity makes particles leave their straight paths. In Einstein’s theory of general relativity, gravity is a distortion of spacetime. Particles still follow the straightest possible paths in that spacetime. But because spacetime is now distorted, even on those straightest paths, particles accelerate as if they were under the influence of what Newton called the gravitational force.










