Is the whole the sum of its parts?

Why Einstein’s famous formula tells us that the whole, as far as mass is concerned, is often less than the sum of its parts

An article by Markus Pössel

Is the whole the sum of its parts? As far as simple physical quantities like mass and energy are concerned, the answer is a definite no. But, perhaps somewhat surprisingly, for those quantities, the whole is commonly less than the sum of its parts. The key to this phenomenon is called binding energy.

Binding energy defined

If a composite object is stable, that is tantamount to saying it won’t spontaneously decay into its component parts. For instance, the nucleus of a helium atom does not spontaneously split into the two protons and two neutrons that are its constituents:

On the contrary, splitting a stable object into its constituents takes some effort. In the language of physics: You need to do some work, invest some energy to pry the constituents apart against the forces that keep them together. But energy doesn’t spontaneously come into existence or vanish. Energy, says a fundamental law of physics, is conserved. In particular the total energy before and after the split of a composite object into its parts must be the same. Thus, we must have:

Energy of the composite object + energy expended to split it up = sum of the energies of the separate parts after the split

We can also move the expended energy to the right side of the equation, which leaves us with

Energy of the composite object = sum of the energies of its parts – energy needed to split the object apart.

At least as far as energies are concerned, this shows that the composite object (in physics lingo: the “bound system”) is less than the sum of its parts. Physicists call the “energy needed to split the object apart” its binding energy.

Binding energy and the mass defect

Enter Einstein and his famous equivalence of energy and (relativistic) mass, expressed in the most famous of all physics formulae: E=mc². According to Einstein, to every energy there corresponds a mass, and to every mass there can be assigned a corresponding energy. If you apply E=mc² (or more precisely the inverse formula m=E/c² giving the mass m corresponding to a given energy E) to our energy equation above, this gives a straightforward result: The relativistic mass of a bound system is somewhat smaller than the sum of the masses of its constituent parts, namely

Mass of bound system = sum of masses of its parts – (binding energy)/c².

The mass of a helium nucleus is thus a bit less than two times the proton mass plus two times the mass of a neutron. The difference, called a mass defect, is a measure for the strength of the bond between the four nucleons: the greater the mass defect, the stronger the energy needed to pry the nucleons apart.

Everyday matter is given its stability by chemical bonds between its atoms and/or molecules. However, such chemical bonds are much too weak, the associated binding energies much too small to result in measurable mass defects – typical values are in the range of a hundredth of thousandth or even of a millionth of the mass of an electron.

The forces binding protons and neutrons together to form atomic nuclei are considerably stronger, with binding energies that are a few million or even billion times larger than those of chemical bonds. In consequence, mass defects correspond to the masses of a few dozen or even a few hundred electrons. That is well within the range of precision mass measurements. The result is a valuable tool for nuclear physicists: they can learn about the properties of the nuclear forces by measuring mass defects of atomic nuclei and derive the corresponding binding energies!

The systematics of nuclear binding energies

Systematic studies of mass defects give some interesting results. A number of them can be read off the following figure. Each of the more than 2000 points plotted there corresponds to one species of atomic nucleus. The horizontal position of the point indicates what is called the mass number of the nucleus: the total number of its neutrons and protons or, to use a technical term, the number of its nucleons. The vertical position stands for the binding energy of the nucleus, divided by the mass number – the “binding energy per nucleon”. The unit for binding energies per nucleon is the Mega-electron-Volt (MeV). One MeV is defined as the energy gained by an electron accelerated by an electrical voltage of one million Volt (it is also the energy corresponding to twice the mass of an electron at rest).

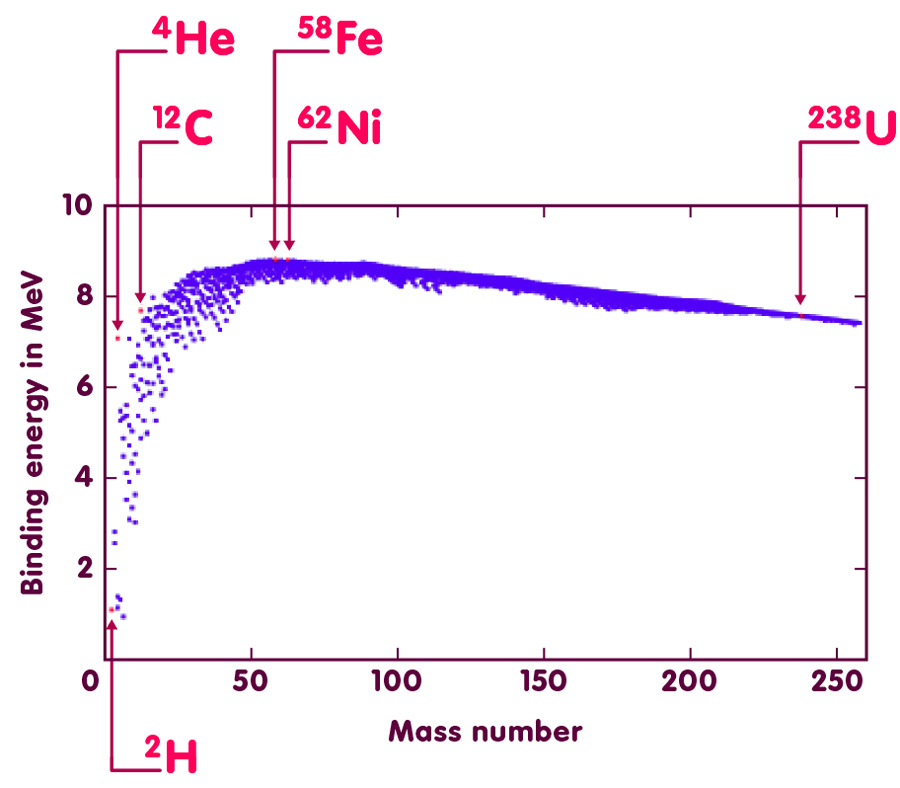
[Information about the data used in this figure]

Evidently, not all atomic nuclei are held together equally tightly. Instead, there are definite trends and a systematic connection between binding energies per nucleon and mass number.

In the left part of the plot, the more massive atomic nuclei (data points further to the right) are in general more tightly bound (higher binding energy per nucleon, data point higher up) than the less massive ones. The consequences? Among others, the fact that Earth is fit for human habitation! With such a trend, fusing lighter atomic nuclei to give heavier nuclei is a process that sets free energy: The total binding energy of the end product is larger than the sum of binding energies of the ingredient nuclei. Binding energy has a negative sign – if, in the end product, it is larger than before, the difference must be set free in the form of ordinary, positive energy. Nuclear fusion processes where this happens are how stars like our sun produce the radiation energy they beam into space. No nuclear fusion means no solar energy, and hence no life on Earth as we know it.

(A sample calculation for the energy released in a nuclear fusion reaction can be found below.)

However, things change when we move further right in the diagram. The more we move to the right, the less efficient further nuclear fusion becomes. We reach the limit with nuclei like iron-58 (iron with 58 nucleons) and nickel-62, which have the highest binding energies per nucleon of all nuclei, and are thus the most stable nuclei in existence.

Beyond those nuclei, the trend reverses. From there on, heavier nuclei are less tightly bound than lighter ones. Fusing nuclei to release energy is thus not an option any more, but splitting up nuclei into smaller nuclei is: In this region, the sum of the binding energy of of lighter nuclei can be larger than the binding energy of the heavier nucleus with the same total number of neutrons and of protons. The energy difference is what is released when the heavier nucleus is split into the lighter nuclei – nuclear fission. Such processes are used in today’s nuclear reactors as well as in nuclear fission bombs (“atomic bombs”).

sample calculation for the energy released in a nuclear fission reaction can be found below.)

But please take note: E=mc² doesn’t give us any explanation for the systematic trends in nuclear binding energies (more about some related misconceptions can be found in the spotlight topic From E=mc² to the atomic bomb). But the direct link between energies and the masses of nuclei can be exploited to measure binding energies, and thus gather data on these systematic trends. E=mc² isn’t the reason for the power of nuclear fission or fusion, but it’s a useful tool for finding out more about these phenomena.

Further Information