Ist das Ganze die Summe seiner Teile?

Wie aus Einsteins berühmter Formel folgt, dass das Ganze in punkto Masse und Energie oft weniger ist als die Summe seiner Teile

Ein Artikel von Markus Pössel

Ist das Ganze die Summe seiner Teile? Selbst, wo es um so einfache physikalische Größen wie Masse und Energie geht, ist die Antwort Nein. Im Gegenteil: Was solche Größen betrifft, ist das Ganze oft weniger als die Summe seiner Teile. Die Antwort hat mit so genannter Bindungsenergie zu tun.

Dass ein zusammengesetztes Objekt „stabil“ ist, heisst nichts anderes, als dass es nicht einfach so im Laufe der Zeit spontan in seine Einzelteile zerfällt. Ein Helium-Atomkern beispielsweise zerfällt nicht einfach in die zwei Protonen und zwei Neutronen, aus denen er zusammengesetzt ist:

Im Gegenteil: Um ein stabiles Objekt in seine Bestandteile zu zerlegen, ist ein gewisser Aufwand nötig. In die Sprache der Physik übersetzt heißt das: Wer das Objekt zerlegen will, muss Energie aufwenden – etwa die Bestandteile auseinanderziehen und dabei die Kräfte überwinden, die sie zusammenhalten. Energie kann nun aber nicht aus dem Nichts entstehen oder verschwinden. In der Energiebilanz für ein Objekt, das wir in seine Einzelteile zerlegen, muss daher auch die Energie auftauchen, die für die Zerlegung aufgewandt haben:

Energie des gebundenen Systems + aufgewendete Energie = Summe der Energien der Einzelteile

oder, wenn man die aufzuwendende Energie auf die rechte Seitung der Gleichung hinüberbringt,

Energie des gebundenen Systems = Summe der Energien der Einzelteile – zur Trennung aufzuwendende Energie

Zumindest energetisch ist das gebundene System damit weniger als die Summe seiner Teile. Die „zur Trennung aufzuwendende Energie“ wird auch Bindungsenergie genannt.

Als nächstes kommt Einsteins berühmte Äquivalenz von Energie und (relativistischer) Masse ins Spiel, ausgedrückt in der Formel E=mc². Danach entspricht jeder Energie eine Masse, und jeder Masse lässt sich eine Energie zuschreiben. Wendet man E=mc² (genauer: die Umkehrung m=E/c², mit der sich die einer gegebenen Energie entsprechende Masse ergibt) auf die obige Gleichung an, dann ist das Ergebnis: Die relativistische Masse des gebundenen Systems ist etwas kleiner als die Summe der Massen der Einzelteile, nämlich

Masse des gebundenen Systems = Summe der Massen der Einzelteile – Bindungsenergie/c².

Ein Heliumatomkern aus zwei Protonen und zwei Neutronen besitzt beispielsweise etwas weniger Masse als zweimal Protonenmasse plus zweimal Neutronenmasse. Die Differenz, der so genannte Massendefekt, ist ein Maß für die Bindungsenergie und damit dafür, wie stark die Bindung der vier Kernteilchen aneinander ist: Je größer die Energie, die zur Zerlegung aufgewendet werden muss, umso stärker die Bindung.

Für chemische Bindungen, wie sie die Atome und Moleküle der uns umgebenden Materie zusammenhalten, ist der Massendefekt freilich unmessbar klein. Typische Massendefekte liegen bei Hunderttausendsteln oder Millionstel der Masse eines Elektrons.

Anders bei den Bindungsenergien der Kernkräfte, die die Protonen und Neutronen eines Atomkerns zusammenhalten. Sie sind millionen- bis milliardenfach grösser. Massendefekte bei Atomkernen entsprechen den Massen einiger Dutzende bis Hunderte von Elektronen. Solche Massenunterschiede sind bei Atomkernen tatsächlich mit großer Genauigkeit messbar. Das schafft ein wichtiges Werkzeug für die Kernphysiker: Durch genaue Messungen der Atomkernmassen können sie genaueres über die Bindungsenergien und damit über die Eigenschaften der Kernkräfte in Erfahrung bringen.

Dabei zeigen sich interessante systematische Effekte. Einige davon lassen sich an der folgenden Abbildung ablesen. Jeder der rund 2000 Punkte darin entspricht einer bestimmten Sorte Atomkern. Dabei ist auf der waagerechten Achse die so genannte Massenzahl des Kerns aufgetragen – die Summe der Zahl der Protonen und der Zahl der Neutronen, aus denen der Kern besteht. Auf der senkrechten Achse ist die Bindungsenergie aufgetragen, geteilt durch die Massenzahl des Kerns – das Ergebnis ist damit die „Bindungsenergie pro Kernteilchen“ und ein ungefähres Maß dafür, wieviel Energie man aufwenden muss, um ein Proton oder Neutron aus dem Atomkern herauszulösen. Einheit der Bindungsenergien sind so genannte Mega-Elektronenvolt, abgekürzt MeV. Definiert ist diese Einheit als die Energie, die ein Elektron gewinnt, wenn es eine elektrische Spannungsdifferenz von einer Million Volt durchläuft. Etwas anschaulicher wird sie durch Einsteins Formel: die Energie 1 MeV entspricht in etwa der doppelten Masse eines Elektrons.

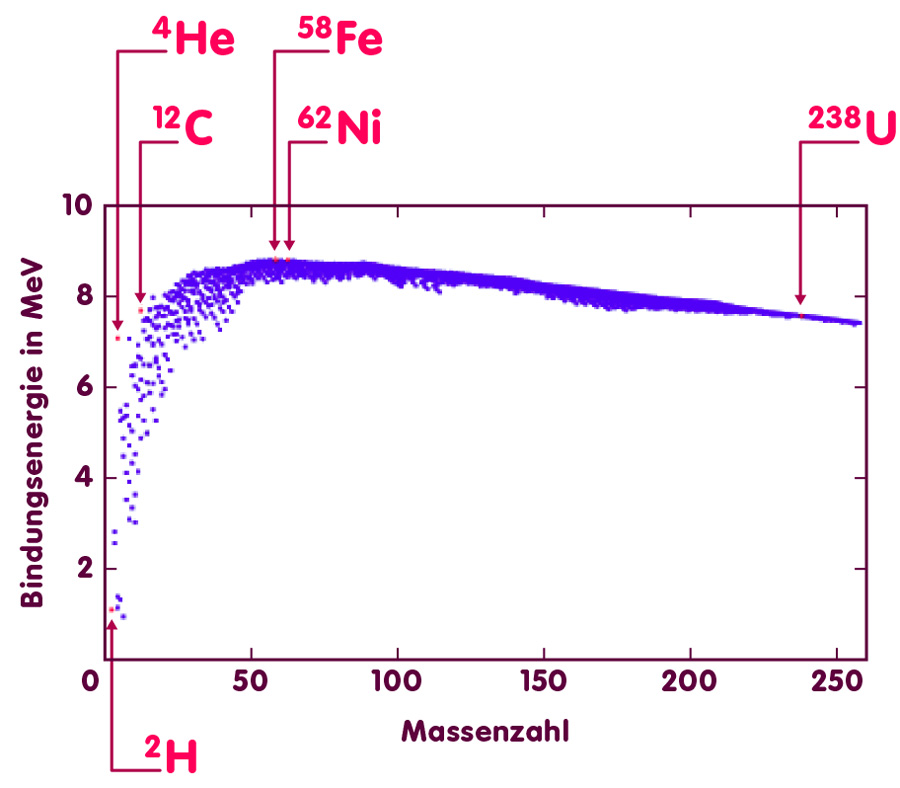
[Informationen zu den zugrundeliegenden Daten]

Interessant ist an diesen Daten, dass die verschiedenen Atomkerne nicht gleich fest zusammenhängen, sondern dass es deutliche systematische Unterschiede bei den Bindungsenergien gibt.

Im linken Teil ist der Trend steigend: Dort sind die massereicheren Atomkerne (höhere Massenzahl, d.h. Datenpunkt weiter rechts) tendenziell auch stärker gebunden (höhere Bindungsenergie pro Proton/Nukleon, d.h. Datenpunkt weiter oben) als leichtere Kerne. Das hat lebenswichtige Konsequenzen, denn es bedeutet, dass bei der Verschmelzung von leichteren Atomkernen zu etwas schwereren Kernen („Kernfusion“) Energie freigesetzt werden kann: Die Bindungsenergie des Endprodukts ist dabei insgesamt größer als die Summen der Bindungsenergien der Ausgangskerne. Bindungsenergie hat ein negatives Vorzeichen – ist die Bindungsenergie am Ende größer, muss der Differenzbetrag in Form normaler, positiver Energie freigesetzt werden. Kernfusionsprozesse, bei denen in solcher Weise durch die Verschmelzung leichter zu schwererer Kerne Energie frei wird, sind die Grundlage der Strahlungsenergieproduktion von Sternen wie unserer Sonne. Ohne Kernfusion keine Sonnenstrahlung und damit auf der Erde kein Leben, wie wir es kennen.

(Zwei Rechenbeispiele zur Energiebilanz der Kernfusion findet sich unten auf dieser Seite.)

Allerdings gilt, wenn man die Kurve nach rechts weiterverfolgt: Je schwerer Atomkerne bereits sind, umso geringer die Energie, die bei einer Fusion freigesetzt wird. Die natürliche Grenze ist bei Kernen wie Eisen (Fe-58) und Nickel (Ni-62) erreicht, den stabilsten Kernen überhaupt. Dort liegt auch in der obigen Abbildung das Maximum der Bindungsenergien pro Kernteilchen.

Geht man noch weiter nach rechts, dann kehrt sich der Trend um: Ab einer gewissen Masse sind die schwereren Atomkerne weniger stark gebunden als die leichteren. Damit können für solche Atomkerne nicht durch Verschmelzung, aber durch Spaltung in mehrere Teilkerne Energie freigesetzt werden: Die Bindungsenergie der Spaltprodukte ist in der Summe größer als die Bindungsenergie des ursprünglichen Kerns. Die Differenzenergie wird bei der Kernspaltung freigesetzt. Solche Prozesse sind die Grundlagen für heutige Kernreaktoren und für die Energiefreisetz durch herkömmliche Atombomben.

(Ein Rechenbeispiel zur Energiebilanz der Kernspaltung findet sich unten auf dieser Seite.)

Wohlgemerkt: Aus E=mc² folgt noch nicht, warum die Bindungsenergien diese Eigenschaften haben (mehr zu dem Irrtum, die Formel etwa für die Energieausbeute der Kernwaffen verantwortlich machen zu wollen, bietet das Vertiefungsthema Von E=mc² zur Atombombe). Aber der Zusammenhang von Energien und Atomkernmassen erlaubt es, die Bindungsenergien indirekt zu messen und so ihrer Systematik auf die Spur zu kommen. E=mc² ist nicht die Begründung für die hohe Energiefreisetzung bei Kernspaltung und Kernfusion, aber ein nützliches Werkzeug zu ihrer Erforschung.

Weitere Informationen