The mathematical universe

Why cosmology is not only a matter for astronomers and physicists, but also for mathematicians

An article by Alan Rendall

Cosmology, the study of the universe as a whole, is not only a matter for astronomers and astrophysicists, but also for mathematicians. At the heart of cosmology, there’s mathematics, and to comprehend the universe, it is not only necessary to observe and measure it, but also to understand its inner workings; it takes not only astronomical data, but also a good understanding of the equations that govern the evolution of the cosmos.

Initial values and evolution

The appropriate physical theory for describing our universe and its gravitational interactions is general relativity. In addition, one needs to take into account models for the properties of matter such as gas and electromagnetic radiation. Together, this defines physical laws which constrain the properties of the cosmos, equations that any universe must obey. A universe that does satisfy the constraints is, in mathematical parlance, a solution to these equations, just as x=-2 and x=4 are solutions to the quadratic equation x² – 2·x-8=0. In general relativity, the gravitational field is described by the Einstein equations and the full system may be referred to as the Einstein-matter equations. These equations determine how a given universe evolves in time, or more precisely: they determine the rate of change of important physical quantities, given their values now.

Whenever the values of these quantities are known at some particular time (the “initial values”), the equations make it possible to determine them at all later times. The determination of solutions in this way, the so-called initial value problem, allows solutions to be specified in a controlled way. It is like having a catalogue of all available solutions of the equations. When specific cosmological models are needed for comparison with astronomical observations, they can be looked for in this catalogue. Mathematics provides the building blocks so that astrophysicists can construct their descriptions of the world.

However, to obtain general knowledge about the equations and their solutions is a difficult mathematical problem which, in our present state of knowledge, is not amenable to a complete solution. One way of making progress is to look at model problems that are especially simple, namely those that contain only very simple forms of matter and pose very special initial values.

Homogeneous universes

A very basic simplification is suggested by astronomical observations: our universe is approximately homogeneous (it is the same at all points of space). As an example, see the following image using data from the 2dF Galaxy Redshift Survey. We, the observers, are at the lower end of the wedge. The wedge-shaped region shows that only part of the sky was searched. Every white dot represents a galaxy, some of them closer to Earth (closer to the sharp end of the wedge), some of them farther away. The greatest distance shown, that of galaxies at the upper boundary, corresponds to a distance of 2 billion light years:

2dF Galaxy Redshift Survey: Homogeneous universe

To be sure, the distribution of galaxies shows a characteristic porous structure, with filaments of higher and regions of lower density. However, subdividing space into cubes a few hundred light-years across, the average density of each cube is the same – on large scales, the universe is homogeneous.

A suitable model universe, simple yet not too far removed from reality, can be obtained by assuming the universe to be exactly homogeneous. Such models are relatively easy to analyse mathematically. Most predictions of modern cosmology make use of these simple models. Yet it is important to remember that they are simplifications. This brings up a question well-known to mathematicians, that of the stability of particular solutions: Is a certain solution a very special case, or is it representative of the more general situation which is the ultimate goal of study? In other words: If some of the assumptions of a special model are relaxed, say, if regions of slightly higher or lower density are introduced into an initially homogeneous universe, does the modified universe behave in a completely different way? Or is the evolution of the simplified model still a good guide to the evolution of the more realistic, slightly inhomogeneous universe? This leads, in particular, to the investigation of initial values which are close to those for a known situation with high symmetry.

De Sitter’s cosmos

A specific example of these general considerations is provided by the situation of accelerated cosmological expansion, which may be associated with a positive cosmological constant or, more generally, with dark energy. There is an explicitly known solution of the Einstein equations with positive cosmological constant and without matter. This is the de Sitter solution, first formulated in 1917, a useful simplified model for a universe with accelerating expansion. Adding homogeneous matter suitable for describing the distribution of galaxies does not greatly alter its qualitative properties – at least with respect to this modification, the solution is stable. Thus, although matter is essential in modelling the cosmos, a matter-free solution can be of great relevance.

In a solution of this kind the distance between galaxies increases exponentially with time, as shown in the following graph:

Exponential growth

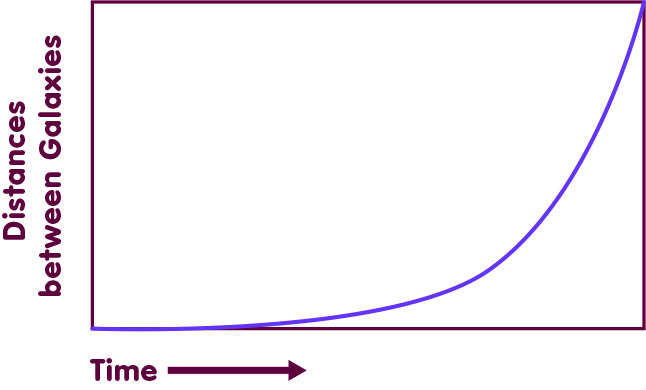
It was proved in 1986 that the de Sitter solution is stable in other respects, at least in the absence of matter: If we disturb its homogeneity by adding weak gravitational waves, corresponding to slight inhomogeneous distortions of the homogeneous spacetime, the result is still an exponentially expanding universe which, at late times, comes closer and closer to the undisturbed de Sitter solution.

To find a similar proof of stability for accelerating universes containing matter is currently an open problem. Heuristic arguments indicate that the presence of matter does not fundamentally change the nature of de Sitter expansion, a statement often referred to as the “cosmic no hair theorem”. The interest of proving this stability is evident, as our own universe falls into this class of universes. Stability would not only provide a rigorous justification for the simplified models currently used. It would also mean that, as in the case without matter, universes like ours should come closer and closer to homogeneity as time goes by. This provides a way of understanding how a homogeneous universe like our own can arise over the course of cosmic evolution, without the need for very special initial conditions. However, the proof used for the matter-free case is not easy to adapt to the new situation, and poses something of a challenge. So far, a proof has only be found for certin cases with symmetry.

At the same time models are being studied where, in addition to ordinary matter representing the galaxies, there is exotic matter with negative pressure known as quintessence – another way of obtaining accelerated expansion, distinct from Einstein’s cosmological constant. Since it is not known in detail what is behind the tendency of our universe to accelerate, it makes sense to keep all options open and study the mathematical properties of large classes of models for dark energy.

Further Information

For the relativistic ideas behind this spotlight topic, check out Elementary Einstein, especially the chapters General Relativity and Cosmology.

Related Spotlights on relativity can be found in the sections General relativity and Cosmology.

More information about the above image showing the distribution of galaxies can be found on the

Website of the 2dF Galaxy Redshift Survey

Colophon

Alan Rendall

is professor of mathematics at Johannes Gutenberg University in Mainz, Germany.

Citation

Cite this article as:
Alan Rendall, “The mathematical universe” in: Einstein Online Band 04 (2010), 01-1022

Definitioner

waves (wave)

In a general sense: any travelling pattern, whether or not it involves matter being transported as well. Simple examples are water-waves - wave crests and troughs travelling over a water surface, and a Mexican wave in a football stadium, with fans alternately standing up and sitting down - the pattern moves throught the stadium, not the fans themselves.

An especially simple form for a wave is a sinus wave, a regular pattern of wave crests and troughs.

time

It is a fact of life that not all events in our universe happen concurrently - instead, there is a certain order. Defining a time coordinate or defining time, the way physicists do it, is to define a prescription to associate with each event a number so as to reflect that order - if event B happens after event A, then the number associated with B should be larger than that associated with A. The first step of this definition is to construct a clock: Choose a simple process that repeats regularly. (What is "regular"? Luckily, in our universe, all elementary processes such as a swinging pendulum, the oscillations of atoms or of electronic circuits lead to the same concept of regularity.) As a second step, install a counter: A mechanism that, with every repetition of the chosen process, raises the count by one. With this definition, one can at least assign a time (the numerical value of the counter) to events happening at location of the clock. For events at different locations, an additional definition is necessary: One needs to define simultaneity. After all, the statement that some far-away event A happens at 12 o'clock is the same as saying that event A and "our clock counter shows 12:00:00" are simultaneous. The how and why of defining simultaneity - a centre-piece of Einstein's special theory of relativity - are described in the spotlight topic Defining "now". With all these preparations, physicists can, in principle, assign a time coordinate value ("a time") to any possible events, and describes how fast or how slow processes happen, compared to that time coordinate.

symmetry

A situation has a symmetry if certain changes make no difference. For instance: a mirror-symmetric image that you view in a mirror looks the same. A perfect sphere looks the same, even if it is rotated around an arbitrary axis through its centre point ("spherical symmetry"). In particle physics, there are more abstract symmetries, less readily pictured, such as supersymmetry.

space

In a strict sense: Space as we know it from everyday life: the totality of all locations in which objects can sit, with three dimensions. In a more general sense used by mathematicians, all kinds of sets of points are spaces - a line for instance, which has but a single dimension, or a two-dimensional surface, but also higher-dimensional spaces. Also, in such more general spaces, geometry can be different from the standard Euclidean geometry taught in high schools - such spaces can be curved.

spacetime

Already in special relativity, observers in motion relative to each other will not, in general, agree as to whether two events happen simultaneously, or as to how great is the distance between two objects. They do, however, agree as to what events there are, although not to when and where they happen. This observer-independent totality of all events is called spacetime. How spacetime is split into space and time can differ from observer to observer. Every-day space has three dimensions. Adding time adds another dimension - spacetime has four dimensions, all in all. We are used to the idea of a point in space - an object that has only one location and is completely defined once its space coordinates are given. In spacetime, a spacetime point is an object defined completely once its space coordinates and its time coordinate are given - which makes a spacetime point nothing but an elementary event. The idea of spacetime is, in addition to its role in special relativity, a building block of general relativity. Analogous to how a plane is flat, but the surface of a sphere is curved, in general relativity, curved or distorted versions of the simple, flat spacetime of special relativity play a role. Spacetime curvature, in general relativity, is intimately connected with gravity. For an introduction to the basics of both theories of relativity, check out the chapters Special relativity and General relativity in Elementary Einstein. Sometimes, it can be helpful to view spacetime in analogy to ordinary space - such analogies are explored in the spotlight topics Time dilation on the road (for time dilation) and Twins on the road (for the twin effect).

solution

In the context of general relativity: a solution or, more precisely, a solution of the Einstein equations is a model universe that follows the law of gravity as prescribed by general relativity. See also exact solution.

relativistic

Models, effects or phenomena in which special relativity or general relativity play a crucial role are called relativistic. Examples are relativistic quantum field theories as theories based on special relativity, or the relativistic perihelion shift as a consequence of general relativity. In addition, conditions under which the difference between relativistic physics and ordinary, classical physics are especially pronounced, are also called relativistic. For instance, when material objects reach speeds close to speed of light, one talks of relativistic speeds, while speeds that are so small compared to light as to make relativistic effects undetectably small are non-relativistic.

pressure

A measure for the strength of the resistance with which matter (for instance a gas) resists attempts to decrease the volume it occupies.

relativistic (perihelion advance, relativistic)

For planetary orbits, there is a small difference between the predictions of Newtonian gravity and general relativity. For instance, in Newton's theory, the orbital curve of a lonely planet orbiting a star is an ellipse. In general relativity, it is a kind of rose or rhodonea curve. Such a curve is similar to an ellipse curve, which shifts a bit with each additional orbit. The shift can be defined by looking at the point which is closest to the sun (perihelion) on each orbit. The additional relativistic shift is, hence, called relativistic perihelion shift or relativistic perihelion advance. A picture can be seen on the page A planet goes astray in the chapter General relativity of Elementary Einstein.

matter

In general relativity: All contents of spacetime that contribute to its curvature: particles, dust, gases, fluids, electromagnetic and other fields. In particle physics: All elementary particles with half-integer spin, such as electrons and quarks, as well as their composites such as protons and neutrons, in contrast with force particles.

light

Light in the strict sense of the word is electromagnetic radiation the human eye can detect, with wave-lengths between 400 and 700 nano metres. In relativity theory and in astronomy, the word is often used in a more general sense, encompassing all kinds of electromagnetic radiation. For instance, astronomers might talk about "infrared light" or "gamma light"; in this context, light in the stricter sense is referred to as "visible light". Within classical physics, the properties of light are governed by Maxwell's equations; in quantum physics, it turns out that light is a stream of energy packets called light quanta or photons. In the context of relativistic physics, light is of great interest, and for a number of reasons. First of all, the speed of light plays a central role in both special and general relativity. Also, there are a number of interesting effects in general relativity which are associated with the propagation of light, namely deflection, the Shapiro effect and the gravitational redshift.

light-years (light-year)

See light-second etc., above

gravitational waves

Distortions of space geometry that propagate through space with the speed of light, analogous to ripples on the surface of a pond propagating as water waves. For more informations about gravitational waves, please consult the chapter Gravitational waves of Elementary Einstein. Selected aspects of gravitational wave physics are described in the category Gravitational waves of our Spotlights on relativity.

general relativity (general theory of relativity)

Albert Einstein's theory of gravity; a generalization of his special theory of relativity. For information about the concepts and applications of this theory, we recommend the chapter general relativity of our introductory section Elementary Einstein. Further information about many different aspects of general relativity and its applications can be found in our section Spotlights on relativity.

gas

In a strict sense: A state of matter in which the atoms and/or molecules wildly careen and collide, without being bound to each other. This movement leads to an inner pressure, while the average kinetic energy of the moving particles is a measure for the temperature of the gas. Compare the other states of matter: solid state, liquid, plasma. In a broader sense, gas is also used to denote other mixtures of freely careening particles, for instance in the case of the electron gas whose pressure stabilizes a white dwarf against further collapse.

galaxy

Stars are rarely found alone - usually, they congregate in conglomerates of millions, billions or even more stars called galaxies. A case in point is our sun, part of a galaxy we call the milky way. The life of a young galaxy can be very turbulent. Examples of such young, active galactic nuclei are radio galaxies and quasars.

free

In the context of relativity theory, a particle (object, observer...) that is not acted upon by any force except gravity is said to be free or, a bit more specific, to be in free fall. Free test particles play an important role in understanding the structure of general relativity.

energy

Physical quantity with the special property that, in physical processes, energy is neither destroyed nor created, simply transformed from one form of energy to another. Some of the different forms of energy that are defined separately are kinetic energy, thermal energy and the energy carried by electromagnetic radiation. Processes that transform one form of energy into another take place in all machines we use in everyday life, from the engine of a subway train (electrical energy into kinetic energy of the train) to an electric blanket (electrical energy into thermal energy). One important consequence of special relativity is that energy and mass are completely equivalent - two different ways to define what is, on closer inspection, one and the same physical quantity. See the keyword equivalence between mass and energy.

Earth

Our very own planet in the solar system - the third planet from the sun. The earth has a mass of about 6 trillion trillion (in exponential notation, 6·10²⁴) kilograms.

density

In a stricter sense synonymous with "mass density": The average density of matter in a region of space is the total mass of all matter contained in that region, divided by the region's volume. More generally, density can refer to other physical quantities as well. The energy density, for instance, is the total sum of energy localized in a region divided by that region's volume.

dark energy

Comparing astronomical observations with the predictions of the big bang models (which link the properties of matter and the speed of the universe's expansion), it turns out that more than 70 percent of the density of the universe is supplied by what is called dark energy, a type of energy that is associated with empty space itself. Ordinary matter or energy are conserved when the universe expands: If I have 10 hydrogen atoms in a certain region of space, and if that region now expands to twice its initial volume, it will still contain no more than the initial 10 hydrogen atoms, now spread over the larger volume. On the other hand, the amount of dark energy in that region of space doubles in the process, just as the volume, the "amount of space" is twice as large than it was in the beginning. There's another crucial difference between ordinary energy and dark energy. The gravitational influence of ordinary masses and ordinary energy is attractive - it is aimed at pulling all the contents of the universe closer together. Dark energy, on the other hand, acts to accelerate the universe's expansion. In that way, it is equivalent to a certain type of what is called a cosmological constant. As yet, nobody knows how (and if) dark energy fits somewhere into our current picture of the fundamental constitutents of the universe, for instance: into the standard model of particle physics or some extension of that model. This makes dark energy one of the greatest mysteries of modern physics.

cosmology

That branch of physics and astronomy dealing with the structure and development of the universe as a whole. At the core of modern cosmology are the big bang models based on Einstein's general theory of relativity. Their basic features are reviewed in the chapter Cosmology of Elementary Einstein. In order to describe the very early universe, it will be necessary to take the effects of quantum gravity into account - this gives rise to models of quantum cosmology.

cosmological constant

In the big bang models, an inherent tendency of space to accelerate or decelerate its expansion. From observations, it seems that our own cosmos has a cosmological constant that leads to a slight acceleration of its expansion.