Die Gravitation der Gravitation
In Einsteins Theorie ist Gravitation ihrerseits eine Gravitationsquelle. Das führt zur so genannten Nichtlinearität der Theorie – der Gravitationseinfluss zweier Körper ist nicht einfach nur die Summe der Einzeleinflüsse!
Ein Artikel von Markus Pössel
Eine der Eigenschaften, wegen derer die Allgemeine Relativitätstheorie deutlich komplizierter ist als die Newtonsche Gravitationstheorie oder die Elektrodynamik ist die so genannte Nichtlinearität: Gravitation kann, grob gesprochen, ihrerseits Gravitation hervorrufen – wo Gravitation im Spiel ist, ist das Ganze definitiv nicht die Summe seiner Teile.
Kräfte, die sich addieren
Stellen Sie sich vor, im Weltraum, fern aller größeren Massen, schwebe eine einsame Massenkugel. Wir können den Gravitationseinfluss, den diese Masse gemäß der Newton’schen Gravitationstheorie auf andere Massen in ihrer Umgebung ausübt (in der Sprache der Physiker: das Feld der Masse) vermessen, indem wir schauen, wie ein kleines Testteilchen von der Massenkugel beeinflusst wird. Dieses Testteilchen möge seinerseits eine so geringe Masse besitzen, dass seine Anwesenheit die Situation nicht merklich verändert. Wir versetzen das Testteilchen an verschiedene Orte und schauen jeweils, wie groß die Gravitationskraft ist, die es von der Massenkugel erfährt.
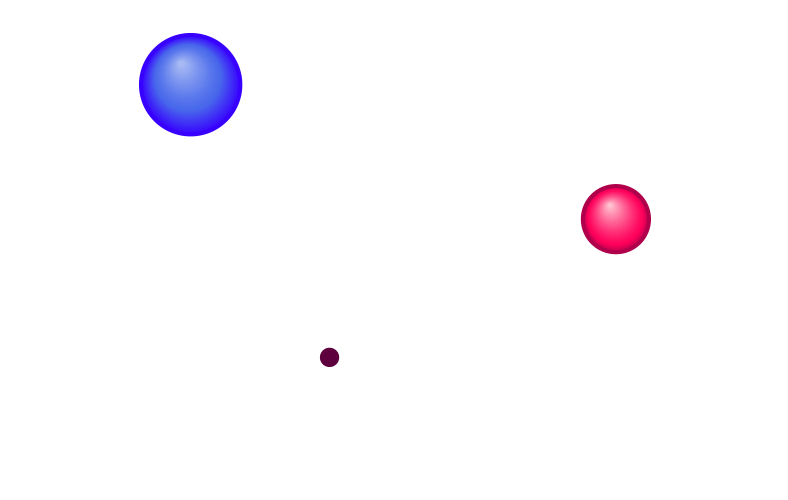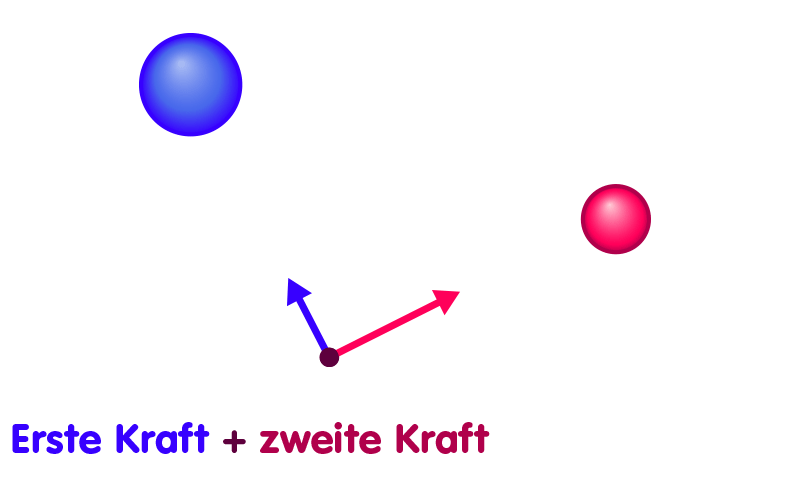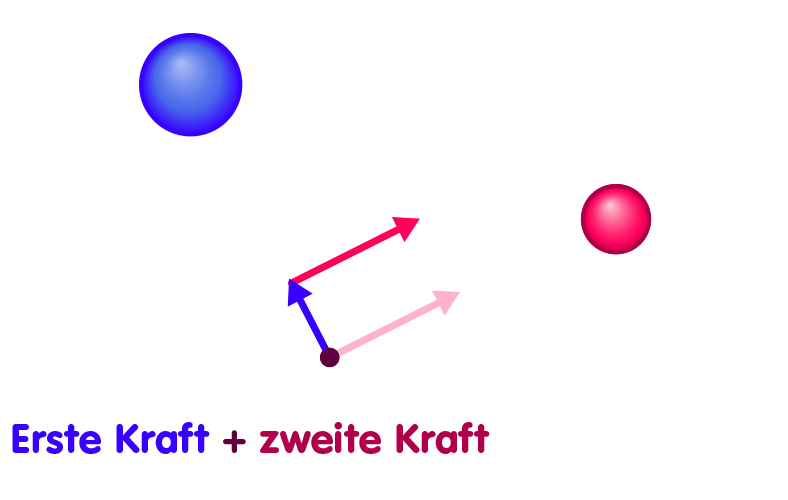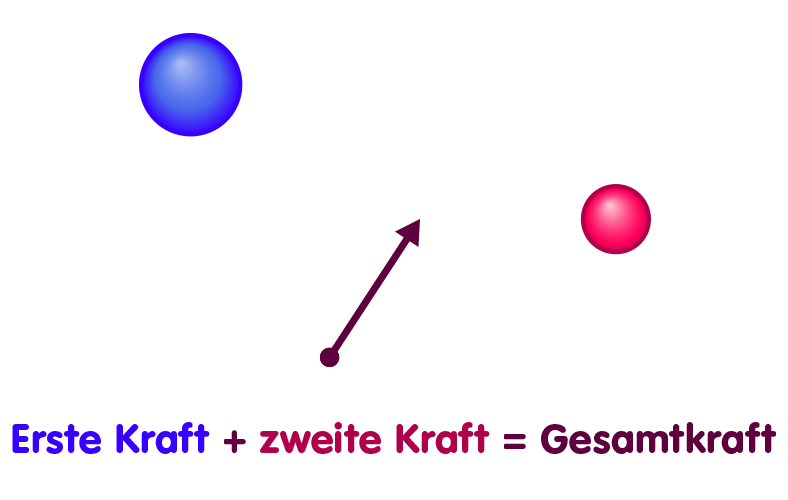
Nehmen wir konkret an, das Testteilchen werde, wenn es sich an einem bestimmten Ort A befindet, von der Massenkugel mit einer Kraftstärke von exakt zwei Newton angezogen. Dies ist in der folgenden Abbildung skizziert, in der die Massenkugel sich am Ort M1 befindet. Der blaue Pfeil steht für die Kraft, die auf das Testteilchen wirkt. Seine Richtung zeigt die Richtung der Kraft an (anziehend, also in Richtung auf die Massenkugel zeigend), während seine Länge die Kraftstärke anzeigt (zwei Newton, nämlich doppelt so lang wie die Referenzstrecke unten links, die ein Newton darstellen soll):

Nun wollen wir die Massenkugel aus dem Spiel nehmen und stattdessen eine andere Massenkugel einführen, deren Position etwas weiter vom Ort A entfernt ist – in der Abbildung also weiter rechts. Diese zweite Kugel möge sogar noch mehr Masse besitzen als die erste, und zwar so viel, dass die Kraft, die sie auf das Testteilchen am Ort A ausübt, trotz der größeren Entfernung sogar noch stärker ist als bei der ersten Massenkugel – ganze drei Newton! Hier ist eine Skizze der neuen Situation, inklusive der neuen Metallkugel am Ort M2:

Nun die entscheidende Frage: Welche Kraft wirkt auf das Testteilchen am Ort A, wenn wir beide Massenkugeln anbringen, jede davon an ihrem früheren Ort (M1 bzw. M2)? Die Antwort ist einfach: Die neue Kraft ist die Summe der beiden Einzelkräfte. Hat das Testteilchen eine Kraft von 2 Newton erfahren, als nur die erste Massenkugel anwesend war, und eine Kraft von 3 Newton allein aufgrund der zweiten, dann ist die Gesamtkraft in Anwesenheit beider Massenkugeln 2+3=5 Newton:

Tatsächlich ist dies nur ein Beispiel für einen allgemeineren Umstand: Wann immer wir die Kräfte kennen, die eine Anordnung A von Massen auf diverse Testteilchen ausübt sowie die entsprechende Wirkung einer zweiten Anordnung von Massen B, kennen wir auch die Gesamtkraft, die wirkt, wenn sowohl die Massen A als auch die Massen B anwesend sind. Für jedes Testteilchen ist die Gesamtkraft die Summe der Kraft, die wirkt, wenn nur die Massen A anwesend sind, plus die Kraft, die in alleiniger Anwesenheit von B wirkt. Ein wenig komplizierter als in unserem einfachen Beispiel ist das Aufsummieren zwar schon, denn im allgemeinen werden die Teilkräfte nicht in ein und dieselbe Richtung wirken. Doch auch für Kräfte in unterschiedliche Richtungen gibt es (Stichwort „Vektorrechnung“) recht einfache Verfahren, eine Summe zu bilden, wie in der folgenden Skizze angedeutet:
Allgemein gilt die Addierbarkeit der Kräfte nur für einen bestimmten Augenblick – einen Schnappschuss, wenn man so will. Wenn sich die beiden Massenkugeln jetzt, in diesem Augenblick, an bestimmten Orten M1 und M2 befinden, dann ist die Gesamtkraft auf das Testteilchen am Ort A die Summe der Kraft, die es erfahren würde, wäre nur die eine Masse an ihrem Ort M1, und der Kraft, wenn nur die andere Masse an M2 anwesend wäre. Auch die Massenkugeln ziehen sich gegenseitig an, und s obald der Augenblick vorbei ist, wird sich ihre Position aufgrund der Anziehung ein wenig verändern. Zu dieser gegenseitigen Beeinflussung kommt es natürlich nicht, solange wirklich nur eine einzige Massenkugel anwesend ist. Mit den veränderten Positionen wird im allgemeinen auch die Kraft auf das Testteilchen etwas anders sein als zuvor. Nichtsdestoweniger gilt auch für jeden neuen Zeitpunkt mit seinen geänderten Kugelpositionen: Wenn wir die Kraft berechnen wollen, die auf das Testteilchen wirkt, müssen wir lediglich die Kräfte addieren, die zu diesem Zeitpunkt von jeder der Kugeln ausgehen.
Die Baukastenwelt der Newton’schen Gravitation
In gewisser Weise wird die Beschreibung der Gravitationskraft damit zu einer Art Legospiel – kompliziertere Anordnungen lassen sich aufbauen, indem man elementare Bausteine miteinander kombiniert. Sobald wir die Elementarbausteine kennen – etwa den Gravitationseinfluss einer sehr kleinen, auf einen winzigen Raumbereich konzentrierten Masse – können wir auch deutlich kompliziertere Situationen beschreiben, ganz einfach indem wir einzelne Teilmassen kombinieren und ihre Kräfte addieren.
Die Elementarbausteine dieser Beschreibung liefert Newtons Gravitationsgesetz, das uns alles sagt, was wir über den Gravitationseinfluss einer kleinen, punktartigen Masse M wissen müssen: Befindet sich im Abstand r von dieser Masse ein Testteilchen mit der Masse m, dann erfährt das Teilchen eine Kraft der Stärke
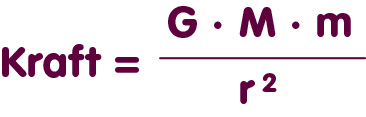
in Richtung von M. Sobald wir diese einfache Formel kennen, lässt sich direkt der Gravitationseinfluss eines ausgedehnten Massekörpers berechnen, wie kompliziert er auch immer geformt sein mag. Dazu müssen wir den Körper lediglich in Gedanken in genügend kleine Bausteine aufteilen. Sind die Bausteine klein genug, dann können wir für jeden davon Newtons gerade angegebene Formel für Punktmassen verwenden, um seinen Gravitationseinfluss zu berechnen. Am Ende müssen wir lediglich die Kraftbeiträge aller Bausteine zusammenzählen.
Auf diese Weise lassen sich eine Reihe interessanter Ergebnisse ableiten. Zum Beispiel kann man so zeigen, dass die Gravitationskraft, die ein beliebiger kugelsymmetrischer Körper auf Objekte in seiner Nachbarschaft ausübt, die gleiche ist, als wäre die gesamte Masse des Körpers in Form eines punktartigen Teilchens im Mittelpunkt der Kugel konzentriert.
In ähnlicher Weise kann man zeigen, dass auf ein Teilchen innerhalb einer Kugelschale (oder irgendeiner anderen hohlen, kugelsymmetrischen Massenanordnung) überhaupt keine Gravitationskraft wirkt.
Man kann die Addierbarkeit auch von einem anderen Standpunkt aus beschreiben, nämlich als Zerlegbarkeit des Gravitationseinflusses. Für eine komplizierte Anordnung von Massekörpern lässt sich in der Newtonschen Theorie genau angeben, welcher Anteil des Gesamt-Gravitationseinflusses auf welchen der Körper zurückgeht.
Linearität
Die Eigenschaft der Addierbarkeit – die Möglichkeit, die Gravitationseinflüsse in komplizierteren Situationen auszurechnen, indem man einfache Bausteine zusammensetzt – heißt auch Linearität.
Der Begriff stammt aus der Mathematik – für eine „lineare Funktion“ f gilt f(x+y)=f(x)+f(y), in Worten: wertet man die Funktion für die Summe zweier Argumente aus, so erhält man dasselbe Ergebnis wie wenn man die Funktion für jeden der Summanden einzeln auswertet und die dabei erhaltenen Werte addiert.
In Bezug auf physikalische Situationen liegt Linearität immer dann vor, wenn die Addition bestimmter Größen die Addition anderer Größen nach sich zieht. In unserem Beispiel hängt die Kraft auf ein Testteilchen von der Masseverteilung ab – Mathematiker würden sagen: sie ist eine Funktion der Massenverteilung. Linear ist die Newton’sche Gravitationstheorie, weil die Addition von zwei Masseverteilungen sich in der Addition der durch sie bewirkten Kräfte äußert.
Die Baukastenwelt der Elektrodynamik
Der Vollständigkeit halber sei angemerkt, dass diese Kombinierbarkeit und Zerlegbarkeit auch für die Elektrodynamik gelten – auch dort addieren sich die von elektrischen Ladungen und/oder Strömen herrührenden elektrischen und magnetischen Kräfte. Allerdings ist die Situation dort in einiger Hinsicht noch komplizierter – beispielsweise ergeben sich die Kräfte auf eine Testladung zu einem gegebenen Augenblick nicht daraus, wo sich die anderen elektrischen Ladungen in diesem Augenblick befinden, sondern man muss berücksichtigen, dass sich die Wirkung dieser anderen Ladungen mit endlicher Geschwindigkeit – genauer: mit Lichtgeschwindigkeit ausbreitet. Das Testteilchen „spürt“ anhand der Kräfte immer erst etwas später, wenn sich die Ladungen bewegt haben.
Besonders einfach zeigt sich die Addierbarkeit und Zerlegbarkeit bei elektromagnetischer Strahlung wie Licht oder Radiowellen. Wenn wir über Antenne Radio hören oder fernsehen nutzen wir jedes Mal aufs Neue aus, dass sich das Gemisch von Radiowellen, das unsere Antenne auffängt, in die Beiträge der verschiedenen Rundfunksender aufteilen lässt, ohne dass die „Tagesschau“, die uns von einem der Sender erreicht, den „BBC World News“ eines anderen Senders in die Quere käme.
Abschied von der Baukastenwelt: Energie als Gravitationsquelle
So praktisch auch die Linearität sein mag – in der Wirklichkeit, die in guter Näherung den Gesetzen der Allgemeinen Relativitätstheorie folgt, ist die Situation eine grundlegend andere. Um einen ungefähren Eindruck davon zu gewinnen, warum dies so ist, genügen Grundkenntnisse der klassischen Physik und der (Speziellen) Relativitätstheorie.
Ein entscheidender Umstand ist, dass Masse und Energie in der Relativitätstheorie äquivalent sind – die Masse, die wir beispielsweise Elementarteilchen zuordnen müssen, ist eine Form von Energie, und umgekehrt kommt jeder Energie eine Masse und damit eine Gravitationswirkung zu (weitere Informationen zu Energie als Gravitationsquelle bietet das Vertiefungsthema Masse und mehr).
Der Umstand, dass Energie eine Quelle von Gravitation ist, hat direkte Konsequenzen für die Zerlegbarkeit des Gravitationseinflusses. Betrachten wir noch einmal ein Testteilchen am Ort A nahe einer Massenkugel:

Der dunkelrote Pfeil zeigt wiederum Richtung und Stärke der Kraft an, mit der die Massenkugel das Testteilchen anzieht.
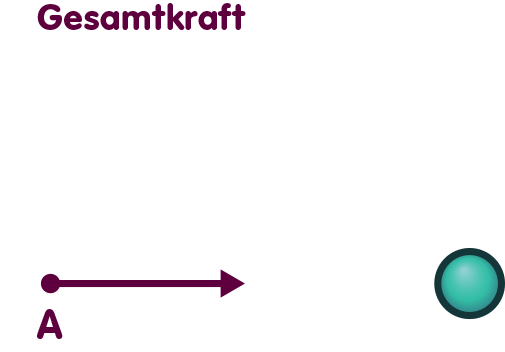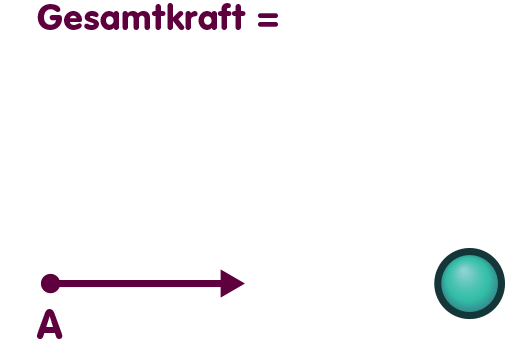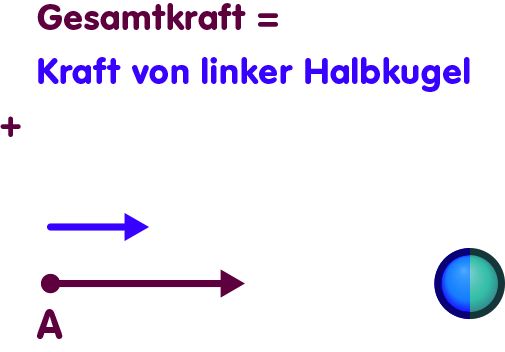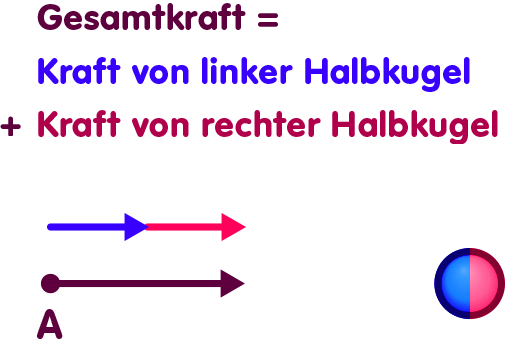
In der Newtonschen Gravitation können wir den Gravitationseinfluss der Massenkugel zerlegen. Nehmen wir an, nur die linke Hälfte der Massenkugel wäre anwesend. Bereits diese Halbkugel würde auf das Testteilchen eine Kraft ausüben, hier durch den blauen Pfeil dargestellt:

Ebenso würde auch die rechte Halbkugel alleine bereits eine Kraft ausüben, siehe den roten Pfeil:

Die Gesamtkraft auf unser Testteilchen ist in der Newtonschen Theorie gleich der Kraft, die die linke Halbkugel ausübt plus die Kraft der rechten Halbkugel:
Doch sobald Energie als Gravitationsquelle wirkt, gilt diese einfache Zerlegung nicht mehr. Um eine Situation zu schaffen, in der beispielsweise nur noch die linke Halbkugel anwesend ist, müssen wir die rechte Halbkugel entfernen. Dazu verschieben wir die rechte Halbkugel immer weiter nach rechts:

Da es sich um ein Gedankenexperiment handelt, können wir die Halbkugel problemlos unendlich weit nach rechts verschieben – dann ist ihr Gravitationseinfluss gleich Null, und wir haben es tatsächlich nur noch mit dem Einfluss der linken Halbkugel auf das Testteilchen zu tun.
Allerdings ziehen sich die beiden Halbkugeln über die Gravitation an. Wir müssen daher eine Kraft aufwenden, um die Halbkugel nach rechts zu transportieren, mit anderen Worten: wir müssen Arbeit verrichten. Das heißt aber wiederum, dass wir dem System Energie zuführen müssen, um die Halbkugeln zu trennen. Im Umkehrschluss besitzt die Vollkugel im Vergleich mit den voneinander getrennten Halbkugeln eine gewisse Bindungsenergie, und zwar mit einem negativen Vorzeichen, denn wir müssen in das System „Vollkugel“ erst noch Energie hineinstecken, um zum System „zwei getrennte Halbkugeln“ zu gelangen. (Etwas detailliertere Ausführungen zum Thema Bindungsenergie liefert das Vertiefungsthema Ist das Ganze die Summe seiner Teile?)
Das heißt aber auch: Der Gravitationseinfluss der Vollkugel ist nicht einfach die Summe der einzelnen Halbkugeln, denn bei der Vollkugel haben wir ganze drei Beiträge: die Masse der linken Halbkugel, die Masse der rechten, und die Bindungsenergie, die das System besitzt, wenn beide Halbkugeln anwesend sind. Da die Bindungsenergie, wie erwähnt, ein negatives Vorzeichen hat, ist die Anziehungskraft der Vollkugel insgesamt etwas schwächer als die Summe der Anziehungskräfte der beiden Halbkugeln.
In unserem Beispiel haben wir den Körper – die Kugel – lediglich zweigeteilt. Das erfasst freilich nur einen Teil der Bindungsenergie, denn auch jede der Halbkugeln lässt sich in zwei oder noch mehr Komponenten aufteilen. Um alle Beiträge zur Bindungsenergie zu erfassen, müssten wir jeden Körper in seine kleinsten Bestandteile zerlegen und aufsummieren, welche Bindungsenergie sich insgesamt ergibt, wenn wir den Körper Stück für Stück aus diesen Einzelteilen zusammensetzen. In der Praxis ist solch eine Zerlegung unmöglich – mit Hilfe von etwas Mathematik lässt sich aber recht direkt ausrechnen, welche Bindungsenergie man einem gegebenen Körper aufgrund der Möglichkeit einer solchen gedachten Zerlegung zuschreiben muss.
Die Allgemeine Relativitätstheorie: eine Theorie mit nichtlinearen Gesetzen
Nähern wir uns der Allgemeinen Relativitätstheorie Schritt für Schritt und betrachten wir zunächst Situationen, in denen die Gravitation vergleichsweise schwach ist. In solchen Situationen weicht die Beschreibung von Raum, Zeit und der Wirkung von Gravitation auf Massekörper nur wenig von denen der Newton’schen Gravitationstheorie ab. In entsprechenden einfachen Situationen (die Physiker mit Hilfe so genannter post-Newtonscher Näherungen beschreiben), und in der Allgemeinen Relativitätstheorie zeigt sich dann tatsächlich, dass die Bindungsenergie als Gravitationsquelle auftritt – ein Beispiel für die „Gravitation der Gravitation“, denn das, was hier als Gravitationsquelle wirkt, geht letztendlich auf die Wirkung der Gravitation selbst zurück!
Gehen wir jetzt zu Situationen über, die keine Entsprechung mehr in der Newton’schen Theorie haben. Gravitationswellen sind ein weiteres Beispiel für die Gravitation der Gravitation: Solche Wellen transportieren Energie und wirken damit als Gravitationsquellen – wenn zwei Gravitationswellen aufeinander stoßen, dann werden sie sich daher nicht einfach ungestört durchdringen, wie es bei elektromagnetischen Wellen der Fall wäre. Stattdessen können die Wellen miteinander wechselwirken, und unter geeigneten Umständen kann sich aus kollidierenden Gravitationswellen sogar ein Schwarzes Loch bilden!
Auch wenn wir die Entwicklung eines Sterns verfolgen, der zu einem Schwarzen Loch kollabiert, spielt die Gravitation der Gravitation eine wichtige Rolle. Während die Materie beim Kollaps immer weiter verdichtet wird, könnte man meinen, ihr Beitrag zur Gravitationswirkung werde immer wichtiger. Tatsächlich spielt die Materie aber in den innersten Regionen des beim Kollaps entstandenen Schwarzen Lochs nur eine Nebenrolle – in unmittelbarer Nähe der Singularität überwiegen Selbstverstärkungseffekte der Raumzeitverzerrung, eben die Gravitation der Gravitation, wenn es darum geht, die Struktur von Raum und Zeit zu bestimmen (siehe hierzu das Vertiefungsthema Singularitäten als Raumzeit-Knetmaschine).
Die Nicht-Addierbarkeit, die daher rührt, dass Gravitation ihrerseits Gravitation hervorruft, lässt sich auch den Einstein-Gleichungen ansehen, die im Rahmen der Allgemeinen Relativitätstheorie beschreiben, wie Gravitation und Gravitationsquellen zusammenhängen. Diese Gleichungen sind nichtlinear – in demselben Sinne, in denen die Gleichung x²=4 nichtlinear ist: Addiert man zwei Werte, welche die Gleichung erfüllen, etwa x=2 und x=-2, dann ist die Summe, x=0, ihrerseits kein x-Wert, der die Gleichung erfüllt. Auf die Einstein-Gleichungen übertragen heißt das in etwa: Die Summe zweier Gravitationsfelder samt zugehöriger Quellen, die jeweils für sich den Einsteinschen Gravitationsgesetzen genügen, ergibt im allgemeinen eine Kombination aus Quellen und Feldern, die diesen Gravitationsgesetzen nicht genügt.
Tatsächlich, und das ist der Grund für das vorsichtige „in etwa“, gehen die Probleme mit der Addierbarkeit sogar noch deutlich tiefer, denn in vielen Situationen lässt sich mit der Begrifflichkeit der Allgemeinen Relativitätstheorie noch nicht einmal angeben, was mit der Summe von verschiedenen „Feldern samt ihren Quellen“ überhaupt gemeint sein soll. In den oben beschriebenen Beispielen mit verschiedenen Massenkugeln haben wir stillschweigend immer eine Hintergrundstruktur von Raum und Zeit vorausgesetzt. Ich hatte beispielsweise die zwei Massenkugeln betreffend gesagt, zu jedem Augenblick (Zeitangabe!) wäre die Kraft auf ein Testteilchen die Summe derjenigen Kraft, die das Testteilchen spürt wenn nur die eine Massenkugeln an der gegebenen Position (im Raum!) anwesend sei und derjenigen Kraft, wenn nur die andere Massenkugel an der gegebenen Position (dito!) anwesend sei. Doch in der Allgemeinen Relativitätstheorie hängt die Geometrie von Raum und Zeit von den darin befindlichen Massen (und anderen Gravitationsquellen) ab. Entfernen wir aus einem Ensemble von Massenkugeln eine der Kugeln, dann werden sich die Abstände der übriggebliebenen Kugeln zu einem gegebenen Testteilchen ändern – und das im allgemeinen so, dass sich die ursprünglichen Abstandsverhältnisse selbst durch Verschieben des Testteilchens nicht wieder herstellen lassen! Unter diesen Umständen ist unser Vorhaben, einzelne Massen zu entfernen und nachzumessen, wie diese Änderung die Kraft auf ein Testteilchen beeinflusst, das an einem bestimmten Ort lokalisiert ist, von vornherein zum Scheitern verurteilt. Was es heißt, Gravitationsquellen zu „addieren“, lässt sich in der Sprache der Theorie noch nicht einmal vernünftig formulieren!
Dieser Umstand lässt sich auch noch anders ausdrücken: In Einsteins Theorie geht es immer gleich um das ganze Universum. Selbst die Beschreibung beispielsweise eines einzelnen Schwarzen Lochs ist im Rahmen der Allgemeinen Relativitätstheorie genau genommen die Beschreibung eines vollständigen Modelluniversums – eines recht einfachen Modelluniversums, zugegeben, da es außer dem Schwarzen Loch keine weiteren Objekte enthält, aber nichtsdestoweniger eines ganzen Universums, dessen Geometrie durch die Anwesenheit des Schwarzen Loches beeinflusst wird. Nicht nur, dass es keine eindeutige Vorschrift dafür gibt, wie ein Universum und ein zweites zu addieren wären (entsprechend dem oben angesprochenen Problem des „selben Ortes“), manchmal gibt es noch nicht einmal eine Möglichkeit, so eine Summation überhaupt vorzunehmen – wie etwa sollte man die Summe eines Urknalluniversums bilden, in dem der Raum analog zu jedem Zeitpunkt nur ein endlich großes Volumen besitzt, und eines unendlich ausgedehnten Modelluniversums, in dessen Mitte ein einsames Schwarzes Loch sitzt?
Umgekehrt gibt es keine allgemein gültige Prozedur, mit der sich innerhalb ein und desselben Universums einzelnen Körpern jeweils ein Anteil an der Gravitationswirkung zuzuweisen ließe. Das Gravitationsfeld lässt sich nur als Ganzes beschreiben und nicht aus Bausteinen zusammensetzen.
Aufgrund der Nichtlinearität – der Gravitation der Gravitation, der Nicht-Kombinierbarkeit und der Nicht-Zerlegbarkeit – ist relativistische Gravitationsphysik deutlich schwieriger als Newton’sche Gravitationstheorie oder Elektrodynamik. Insbesondere gibt es keine allgemeine Möglichkeit, kompliziertere Situationen aus einfacheren Bausteinen aufzubauen – für jede komplizierte Situation muss neu gerechnet werden. Wer weisß wie sich Testteilchen in der Nähe zweier verschiedener einzelner Schwarzer Löcher verhalten, weiß noch lange nicht, wie sich die betreffenden Teilchen verhalten würden, wenn beide Schwarzen Löcher gleichzeitig anwesend wären.
Weitere Informationen
Eine Einführung in die Grundlagen der Einstein’schen Gravitationstheorie bietet der Abschnitt Allgemeine Relativitätstheorie von Einstein für Einsteiger.
Verwandte Vertiefungsthemen finden sich im Abschnitt Allgemeine Relativitätstheorie.
Kolophon
ist Astrophysiker am Max-Planck-Institut für Astronomie, Leiter des Hauses der Astronomie in Heidelberg und Initiator von Einstein Online.
Zitierung
Zu zitieren als:
Markus Pössel, “Die Gravitation der Gravitation” in: Einstein Online Band 03 (2007), 03-1101








