The gravity of gravity

An important property of gravity in Einstein’s theory is that it can create more gravity. The result is “non-linearity” – the gravitational influence of two bodies isn’t just the sum of their separate influences!

An article by Markus Pössel

One reason why the physics of general relativity is much more difficult than that of Newton’s theory of gravity or the theory of electrodynamics is a property called non-linearity. In short, gravity can beget further gravity – where gravitational systems are concerned, the whole is not the sum of its parts.

Adding forces

Imagine that we are in deep space, far away from all sizeable masses such as planets or stars. In front of us, there is a sphere drifting in space. We can chart the gravitational influence which this sphere exerts on other masses in its vicinity (in physics-speak, the sphere’s gravitational field) by keeping a record of its influence on a small test particle. The particle’s mass is so little that its presence does not significantly alter the situation. Thus, we can use the particle as a probe – we keep track of the force exerted by the spherical mass as we move the particle to different locations.

As an example, say that when our test particle is at location A, the gravitational force pulling it towards the sphere has a magnitude of two Newton. Here is a sketch showing the sphere on the right at the location M1 and the test particle on the left at location A. The force on the test particle is represented by the blue arrow – the arrow’s direction shows the direction of the force (an attractive force, so the arrow points towards the sphere) and its length represents the magnitude of the force (in this case two Newton – twice as long as the reference length representing one Newton, shown on the bottom left):

Now let us take away the first sphere and replace it by a different sphere located a bit further to the right. The second sphere is more massive than the first, so the force it exerts on the test particle at location A is a bit larger: a whopping 3 Newton! Here is a sketch of this second situation, with the second sphere at location M2:

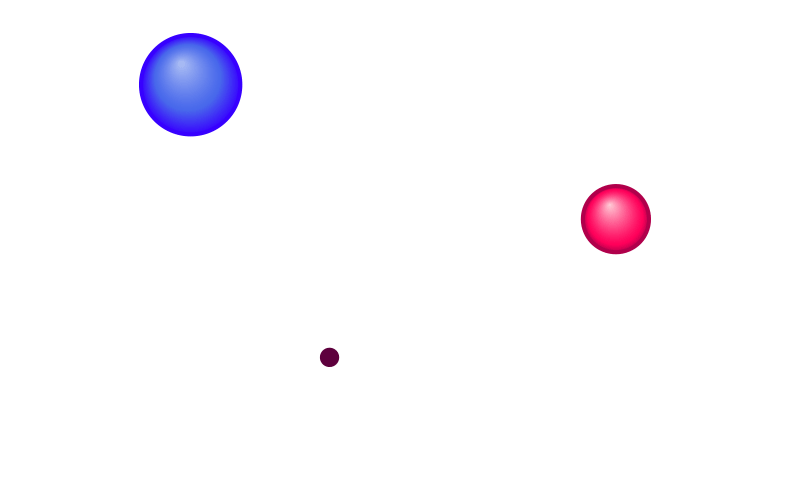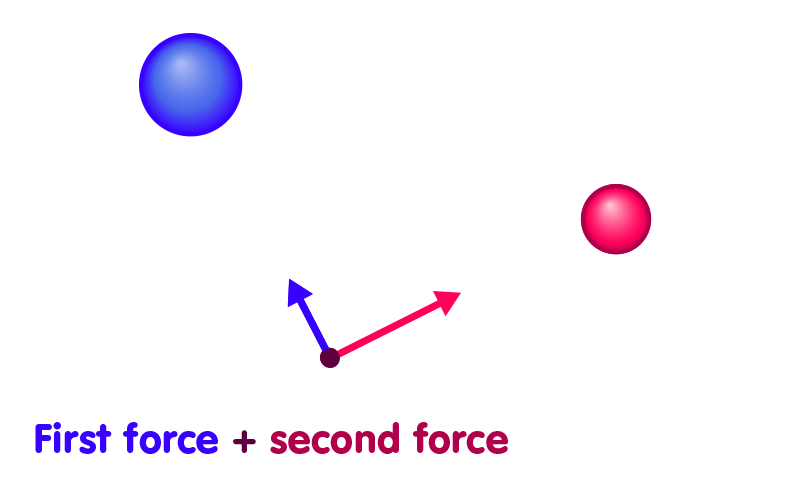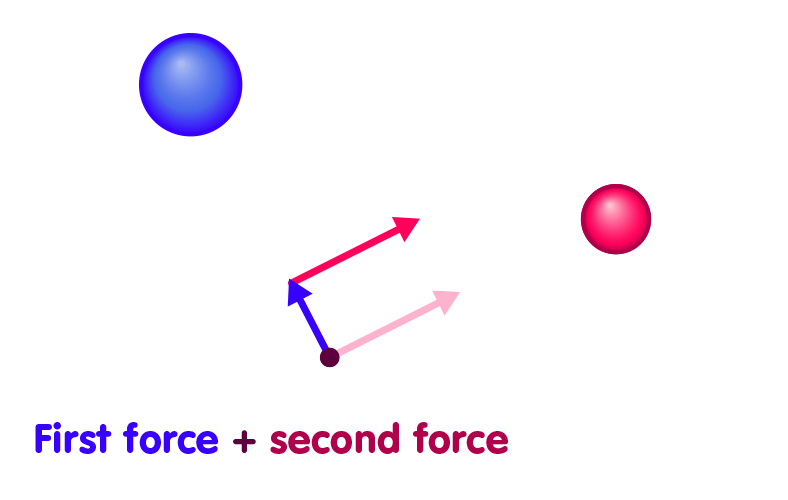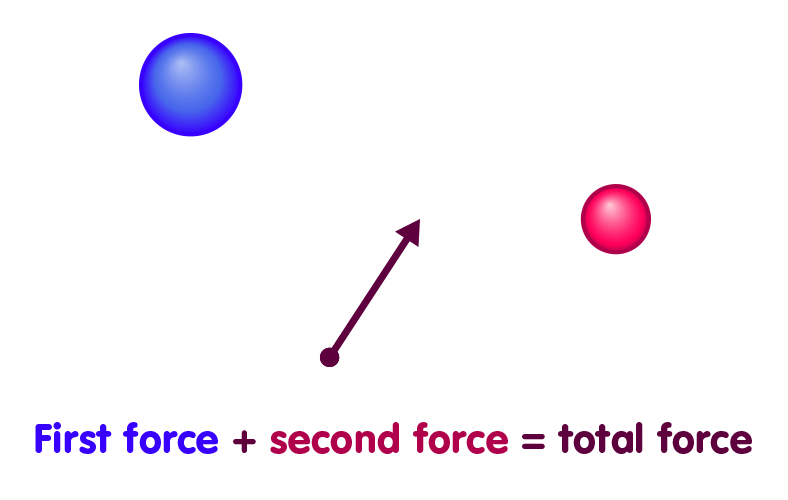
Now the crucial question – if we place both spheres at their respective locations M1 and M2, what will be the force on our test particle at location A? The answer is simple and direct: The new force is the sum of the two separate forces. If the particle has experienced a force of 2 Newton when only the first sphere was present, and a force of 3 Newton when only the second sphere was, then it now experiences a force of 5 Newton:

This is an example for a more general rule: If we know the forces exerted by one particular mass configuration, and the forces exerted by a second configuration, then we also know the forces when all of the masses, of both configurations, are present. It is simply the sum of the force exerted by the first configuration and that exerted by the second one. To be sure, the situation will often be a bit more complicated than in our simple example, as the two forces which are to be added up do not usually point in the same direction. But there are some simple mathematical rules (“vector addition”) for adding up forces that pull or push in different directions, so all is well, as sketched here:

In general, this addition of forces is only valid for one specific moment in time. If the two massive spheres are now, at this moment, at the locations M1 and M2, then the total force on the test particle at location A is the sum of the force it would have experienced if only the first mass had been at its location M1, plus the force if only the second mass had been at M2. But the two masses are attracting each other as well, so as soon as this moment passes, the two massive spheres will move towards each other, changing their position – something that certainly doesn’t happen as long as only one of them is around. As their positions change, so will the force on the test particle. Nevertheless, at each later moment, the same law of addition holds: In order to calculate the total force, we need to determine for each sphere the force which it exerts from its new location, and add all those forces up.

The building blocks of Newtonian gravity

In this way, the description of the gravitational force becomes a matter of building blocks. Once you have an elementary building block – the force exerted by a small mass in a tiny region of space – you can build up the gravitational influence of more complex configuration simply by dividing it into smaller masses and adding up all the different partial forces.

The elementary building block is given by Newton’s law of gravity, which tells us all we need to know about the gravitational influence of a small, point-like mass M. If there is a test particle with mass m a distance r away from our point-like mass M, then there is a gravitational force between them, with a magnitude

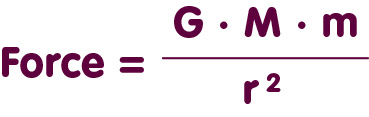
Once we know this simple formula, it is straightforward to calculate the gravitational influence of any massive body, however complicated its shape. We simply view the body as a collection of building blocks. If those building blocks are small enough, the force they exert will be given by Newton’s formula for point-like masses. Once we have calculated the force exerted by each building block, we simply add up all the force contributions.

In this way, one can derive a number of interesting results. For instance, it is possible to show that the gravitational force with which an arbitrary, spherically symmetric body acts on objects in its vicinity is the same as if it were point-like, all its mass concentrated in the center of the sphere.

In the same way, one can show that inside the hollow interior of a spherical shell (or any other spherically symmetric hollow mass configuration), there are no gravitational forces at all.

The building block structure also means that, in Newtonian gravity, we can clearly apportion responsibility: For every configuration of masses, we can clearly determine each mass’s contribution to the configuration’s overall gravitational influence. For an extended body, we can clearly state for each portion of that body the contribution that it makes to the overall gravitational attraction.

Linearity

The building block property – the possibility of calculating the total gravitational force by adding up different contributions – is also known as linearity. The property of “combinability by mere addition”, of being able to construct electromagnetic or gravitational influences in more complex situation by combining simpler building blocks, is called linearity.

“Linearity” is a mathematical term. For a “linear function” f, we have f(x+y)=f(x)+f(y) – evaluating the function on the sum of two arguments gives the same result as adding the function value for the first and for the second argument.

In physics, there is linearity whenever adding up one specific physical quantity means we can also add up other, related quantities. In our example, the force on a test particle depends on the distribution of masses – mathematicians would say: it is a function of what masses are present. Newtonian gravity is linear since if we add two mass distributions, the forces they exert on a given test particle add up as well.

The building blocks of electrodynamics

For completeness, it should be noted that this linearity also applies to electrodynamics, where the electric and magnetic forces produced by different electric charges or currents add up, as well. However, in some respects the situation is more complicated – notably, the force felt by a test particle does not result from where the other electric charges are at that particular moment in time; instead, you have to take into account that the influence of these charges propagates at finite speed – the speed of light. If the charges move, the test particle will “feel” the change only some time later.

The simplest example for linearity in electrodynamics are electromagnetic waves such as light or radio waves. Whenever we use an antenna to receive radio or TV programs, we rely on the fact that radio waves add up linearly: Different signals broadcast from different locations simply add up – they do not influence or distort each other -, and upon receiving them with an antenna, they are readily separated into signals from, say, the BBC World Service on the one hand and a local radio station on the other.

Goodbye to the building blocks: Energy as a source of gravity

While linearity has great practical advantages – reality, which closely follows the laws set down by general relativity, works in a different way. With some basic knowledge in classical physics as well as (special) relativity, it is straightforward to see why.

The crucial fact is that, in relativity, mass and energy are equivalent – the mass associated with some elementary particle is also a form of energy, and conversely, every other form of energy corresponds to some mass, and hence serves as a source of gravity (some more information about this can be found in the spotlight text Mass and more).

The fact that energy is a source of gravity is of crucial importance when we try to analyze a body’s gravitational influence, assigning responsibility for components of the total force to different portions of the body. Let’s examine a test particle at a location A near a spherical mass:

Once more, the dark red arrow represents the direction and strength of the force acting on the test particle and pulling it towards the sphere.

In Newtonian gravity, we can decompose the spherical mass’s gravitational influence. Assume that only the left half of the sphere is present. This half will exert a force on our test particle, which is represented below by the blue arrow:

In the same way, the left hemisphere alone would exert a force, represented here by the red arrow:

In Newtonian gravity, the force exerted by the sphere is simply the sum of the forces exerted by the left and by the right hemisphere:

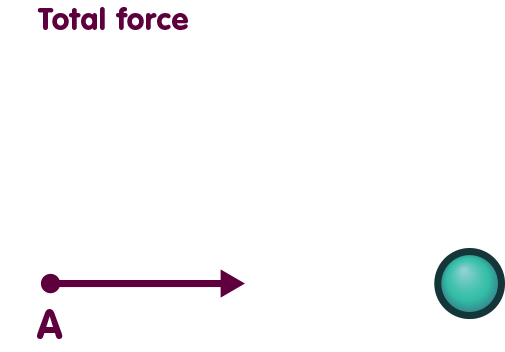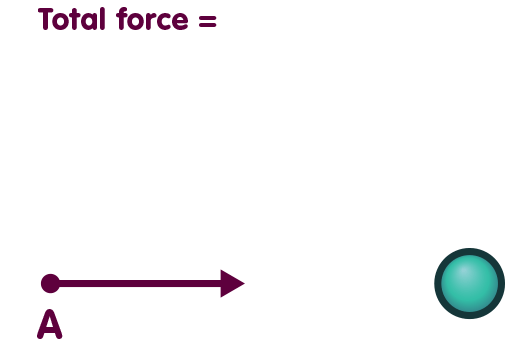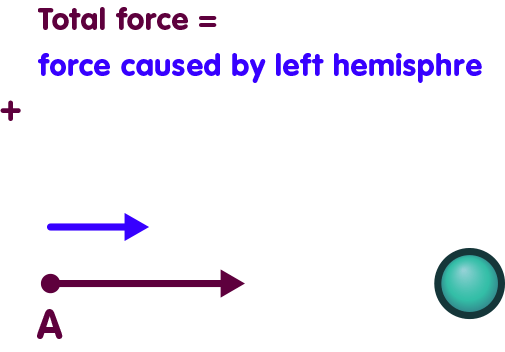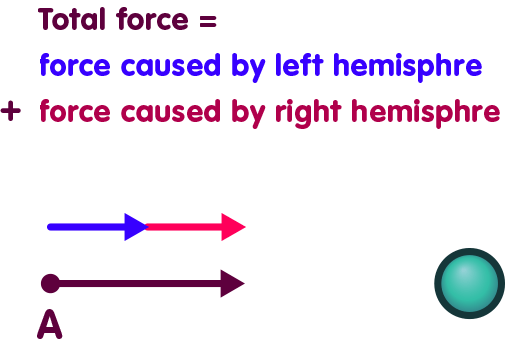
But as soon as energy acts as a source of gravity, matters become more complicated. In order to create a situation in which only, say, the left hemisphere is present, we can grab the right hemisphere and transport it away:

Since this is only a thought experiment, we can remove the right hemisphere completely – by moving it infinitely far away, so that its gravitational influence dwindles to zero and we are left only with the left hemisphere and its influence on the test particles.

But the two hemispheres attract each other gravitationally as well, so in order to spirit the right hemisphere away, we must do work – we must use force while we pull the sphere away. Another way of saying this is that we must add energy to the system in order to seperate the two hemispheres and remove the right one. Conversely, this means that when they were together forming a solid sphere, the two hemispheres had a certain binding energy. That binding energy is negative, since we must add energy to the system “complete sphere” in order to obtain a system “two separated hemispheres”. (More about binding energy can be found in the spotlight text Is the whole the sum of its parts?)

Another consequence is the following: The gravitational influence of the sphere is not simply the sum of the influence of the two hemispheres, since there are three contributions as we make the transition from the two hemispheres to the full sphere: the mass of one hemisphere, that of the other, and the binding energy we must assign to the system when both hemispheres are present. The binding energy is negative, so all in all the gravitational pull of the full sphere is a bit less than the sum of the forces exerted by each hemisphere on its own.

In our simple example, we have merely bisected the sphere into two hemispheres. In that way, we can only calculate part of the sphere’s binding energy. In order to obtain all of it, we would need to divide each body into the smallest possible parts and sum up all the different contributions to the binding energy as we reconstruct the body, piece by piece. While this is impossible to do in practice, it takes only a little math to calculate the binding energy that needs to be assigned to a given body as you rebuild it from an infinite number of infinitesimal pieces.

General relativity: a theory with non-linear laws

Let us approach general relativity step by step, starting with situations in which gravity is comparatively weak. In such situations, the predictions of general relativity differ only by very little from those of Newtonian gravity. Physicists describe such situations using what are called post-Newtonian approximations, which systematically add general relativistic effects to a scenario initially described with the help of Newton’s theory. In such descriptions, one of the things to notice is that, binding energy indeed serves as a source of gravity – an example for the “gravity of gravity”, since in the last analysis, gravity itself is responsible for this particular source of further gravity.

Next, we can take a look at situations which have no counterpart in Newtonian physics. A prime example are gravitational waves, and these are also an example for the gravity of gravity: As such waves propagate, energy is transported through space. But energy is a source of gravity, so when two gravitational waves meet, they do not just pass through each other, they interact. If both waves are weak, the interaction will be almost unnoticeable, but for stronger waves, the consequences can be quite dramatic – in some cases, the collision of two gravitational waves could lead to the formation of a black hole!

Speaking of black holes, the collapse of a star to form such an object is another example where the gravity of gravity becomes important. You might think that during such a collapse, as matter becomes compressed further and further, its contribution to local gravity would become more and more important. But in fact, that is not the case – on the contrary, in the innermost regions of the collapse, close to the black hole’s singularity, the gravity of gravity itself is mostly responsible for the structure of space and time (more about this can be found in the spotlight text Of singularities and breadmaking.

That gravitational sources do not simply add up – that there is such a thing as the gravity of gravity – can also be seen directly in Einstein’s equations, Einstein’s recipe for how matter and other sources of gravity interact with the geometry of spacetime. These equations are non-linear in the same sense that the equation x²=4 is nonlinear. If you add two values for x which satisfy the equation, say x=-2 and x=2, then the result x=0 will not satisfy the equation as well. In the case of Einstein’s equations, this corresponds to a statement somewhat like the following: If you add up two gravitational fields, including their sources, where each field-source-combination obeys Einstein’s equations, then the sum will not be another combination of fields and sources compatible with Einstein’s laws of gravity.

In fact (and this is the reason for the cautious “somewhat” in the previous sentence), in general relativity, there are even more fundamental problems when it comes to adding up sources. In many situations, using the concepts of general relativity, you cannot even state what it means to add up “fields including their sources”. All the simple examples above presuppose a background structure of space and time. We talked about two spherical masses and stated that, at a given moment in time, the total force is the sum of the force when only one of the spheres is present at its given location in space plus the corresponding force for the other sphere. This only makes sense if it is possible to specify what the “given location” is, and what the “given moment in time”. But in general relativity, the geometry of space and time is influenced by sources of gravity. Imagine some configuration of masses. If I remove one of them, then the distances of the others to some specific test particle will automatically change. Could I simply move the test particle around, restoring its original distances to the remaining masses? In general, not even that will be possible – restoring some of the distances to their original values will necessarily cause the distances to some of the other masses be different. Under these circumstances, there is not even a sensible definition of what it means to remove one of the spheres and examine how that removal affects the gravitational attraction acting on a test particle in one and the same location.

There is another way of putting this. In Einstein’s theory, you’re always dealing with complete universes. Even if you use the theory to describe a single black hole, then strictly speaking what you are describing is a very simple, but nonetheless complete model universe – a universe containing a black hole and nothing else. Throughout that universe, the geometry of space and time is influenced by the black hole. Not only is there no uniquely defined way to add two universes – how will you decide which location in one of the universes is “the same” as a given location in the other universe? In many examples, such an addition seems completely impossible – for instance, how could you possibly add a big bang universe for which the volume of space is finite, and an infinitely extended model universe containing a single black hole?

Vice versa, even within a single universe there is no general procedure for identifying the extent to which one of many bodies contained in that universe contributes to gravity. The gravitational field can only be described as a whole. It cannot be constructed from more elementary building blocks.

Non-linearity makes relativistic physics more difficult than Newtonian gravity or electrodynamics. There is no general way of building up more complex situations from elementary building blocks. For each complex situation, the calculations must start anew. If you know how a test particle would move in the vicinity of two different single black holes, that does not tell you what gravity the particle would feel if both black holes were present.

Further Information