Spacetime singularities
Information about the most disturbing feature of Einstein’s theory – ragged edges of spacetime known as singularities.
An article by Claes Uggla
Perhaps the most drastic consequence of Einstein’s description of gravity in terms of curved spacetime geometry in the framework of his general theory of relativity is the possibility that space and time may exhibit “holes” or “edges”: spacetime singularities.
Over the edge
Unfortunately it is not so easy to give a precise meaning to what this means. In other physical theories, singularities are defined as some kind of “pathological behavior” that takes place on an orderly stage provided by space and time. For instance, a model describing a fluid might predict that, under certain conditions, the pressure becomes infinitely large somewhere at some time – clearly at odds with reality. But in general relativity, spacetime itself behaves pathologically, and it can do so in many ways.
According to the present standard definition, a spacetime singularity can be identified by examining particles in free fall – both ordinary matter particles and massless particles like photons. In general relativity, such freely falling particles, which by definition are only affected by gravity and by no other forces, move on the straightest possible lines through spacetime, on what mathematicians call geodesics. A spacetime singularity is said to occur wherever a freely falling particle suddenly pops out of existence! Since the particle travels through spacetime in the straightest possible way, namely on a geodesic, and since the abrupt end of the particle’s existence corresponds to the unexpected end of that geodesic motion, this phenomenon is called geodesic incompleteness.
It may be helpful to consider the following two-dimensional analogy: Take a sheet of paper – a simple two-dimensional surface. A geodesic on such a sheet of paper is just a straight line. Geodesic motion on the piece of paper analogous to a particle in free fall can be illustrated by continuing a straight line in the straightest possible way. If our piece of paper were of infinite extent, then we could simply continue each straight line as far as we liked:

Geodesic motion – analogy: Using pencil and ruler to prolong a given small portion of a straight line on a piece of paper.
Not so if our piece of paper has a hole or an edge, as in the following animation:

Geodesic incompleteness – analogy: As the pencil reaches the edge of a piece of paper, a given straight line cannot be continued any further.
Where there is no paper, there is no way to continue, and our straight line must come to an abrupt end – the geodesic is incomplete.
Most people would agree that it is strange that particles in free fall suddenly disappear. Surely it is reason enough to denote such a pathological spacetime as singular, in the sense of “unusual,” “peculiar,” or “odd.”
As an aside, note that this definition of singularities does not encompass all conceivable spacetime pathologies. In a spacetime that is, by our definition, free of singularities, particles in free fall will behave normally, yet we might still encounter very odd behaviour by, say, accelerating particles. For instance, an accelerating rocket – which, due to the action of its booster engines, is definitely not in free fall – could suddenly disappear. However, having noted this limitation of our definition, let us leave this different kind of weirdness aside and concentrate on the pathologies characterized by geodesic incompleteness.
The rule or the exception?
Within the framework of general relativity, do geodesically incomplete spacetimes actually exist? Perhaps singular spacetimes are forbidden by Einstein’s equations? And if not, are they anything more than mere mathematical oddities of no practical significance? Perhaps they only occur in unrealistic, highly idealized models: For instance, it could be that only perfectly spherically symmetric collapsing stars lead to the formation of black holes with a singularity inside, but such idealized symmetric collapses never happen in the real world, where there is always some deviation from symmetry.
Amazingly, singularities are indeed allowed in general relativity and, moreover, they occur in a wide range of realistic models, notably at the beginning of an expanding universe such as ours (a “big bang singularity”) and in the interior of black holes, even those formed through realistic non-symmetric collapse. This has been established in a number of celebrated mathematical theorems called singularity theorems – the first and most famous obtained in the mid-sixties by Roger Penrose and Stephen Hawking.
The strength of these theorems is that they are very general. Their proofs only rely on one, out of several, of Einstein’s general relativistic equations, as well as on some physically reasonable assumptions about the properties of matter. Their strength is also their weakness; because of the few assumptions they only tell us that singularities occur – they hardly say anything about the nature of the singularities – in particular, they do not give any information about the birth of the universe or what would happen if you fell into a black hole.
Two types of singularities
So what is the possible nature of these singularities? As a first step towards an understanding, it is convenient to divide spacetime singularities into two main categories: curvature singularities, for which spacetime curvature grows beyond all bounds (“blows up”), and singularities for which this does not happen.
Curvature is associated with gravity and hence curvature singularities correspond to “infinitely strong gravity.” There are several possibilities of how such infinitely strong gravity can manifest itself. For instance, it could be that the energy density becomes infinitely large – this is called a “Ricci singularity”, after the Italian mathematician Gregorio Ricci-Curbastro who, in the late nineteenth and early twentieth century, played a key role in the development of differential geometry. As an example of a Ricci singularity, the following graph shows – in a qualitative manner – the evolution of energy density in a universe described by a big bang model. As you go towards the left – corresponding to earlier and earlier instances of cosmic time zero – the density grows beyond all bounds, and at cosmic time zero – at the big bang – it was infinitely high:
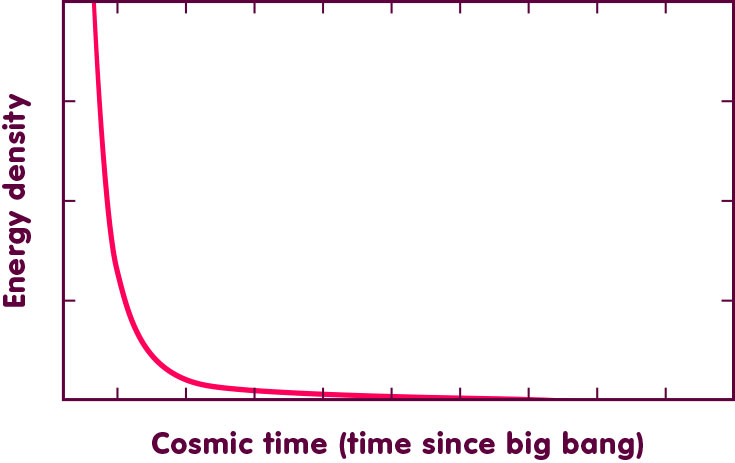
Or it could be that, even without the energy density becoming infinite, the tidal forces (differences in gravity that squeeze or stretch an extended object in different directions) become infinitely large – a “Weyl singularity”, named after the German mathematician Hermann Weyl who, soon after Einstein’s initial publication, was one of the first to explore the rich interplay between relativity and differential geometry.
Now for the second case: A simple example of a non-curvature singularity is what is called a conical singularity, obtained by taking a flat spacetime (a spacetime not distorted by gravity at all), cutting out a wedge-shaped region and gluing together the wedge boundaries. Let us again provide an analogous example by means of a two-dimensional piece of paper as in this illustration:
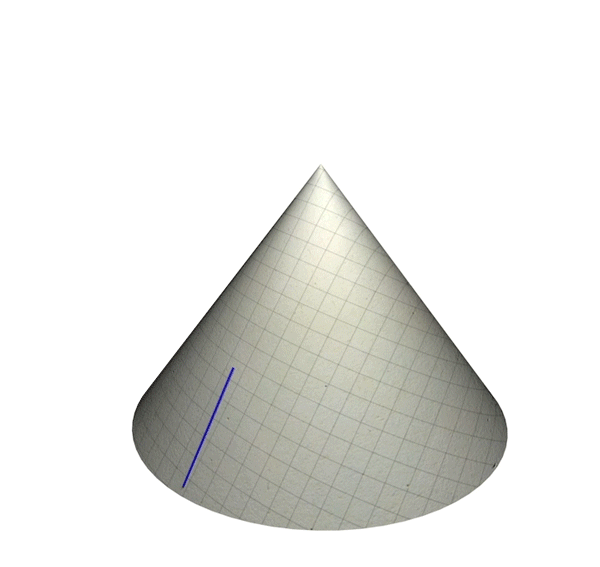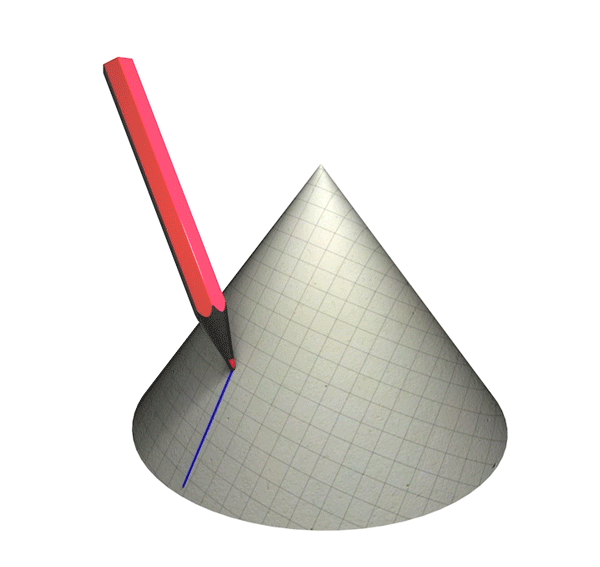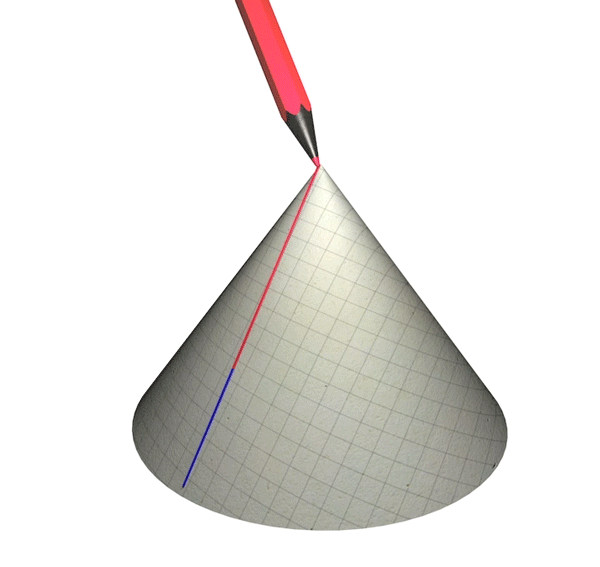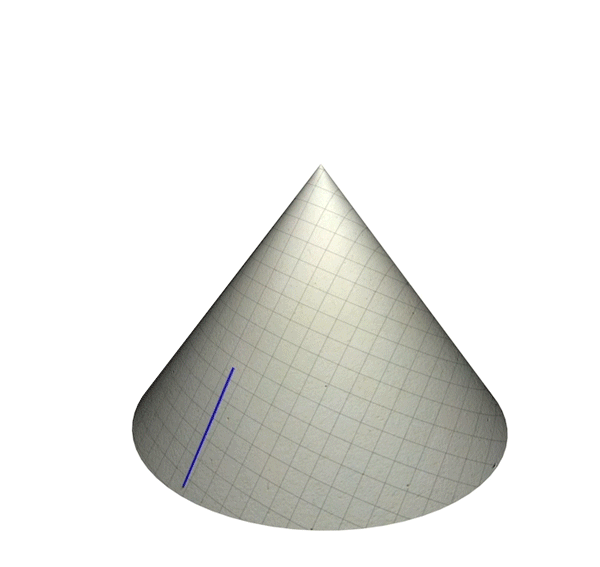
Conical singularity – analogy: A straight line that reaches the tip of a cone cannot be continued any further
In this case curvature is zero everywhere – the paper is flat. Still, at the tip of the cone, there is a singularity: If you draw a straight line that runs into the tip, there is no way to continue that straight line any further – the line is geodesically incomplete.
While this example shows how, even in flat space, there can be singular holes or edges, such non-curvature singularities are unlikely to be of physical importance. Instead, the singularities of relevance to physics are expected to be curvature singularities connected with ultra-strong gravity in the early universe or in the interior of black holes.
To understand what happens when one encounters such a “physical” singularity requires more information than what goes into the singularity theorems and this complicates things further; the ways in which things can “go wrong” with space and time, when our universe was born or when a star collapses to a black hole, are the subject of intense research. (Some more information about this can be found in the spotlight text The nature of singularities.)
Further Information
Relativistic background information for this Spotlight topic can be found in Elementary Einstein, in particular in the chapter General relativity.
Further related Spotlights on relativity can be found in the category General relativity.
Colophon
is a professor of theoretical physics at Karlstad University.
Citation
Cite this article as:
Claes Uggla, “Spacetime singularities” in: Einstein Online Band 02 (2006), 02-1002










