Glossary
In systems consisting of many particles, be they solid bodies, fluids or gases, the constitutents are in constant, chaotic motion: the atoms in a solid crystal oscillate a bit, the molecules of a gas are in rapid, disordered motion, and so on. The average energy with which each constitutent contributes to every part of the disorderly motion is the same, and it is called the temperature of the system. High average energy corresponds to high temperature – atoms vibrating wildly, gas molecules zipping around very fast -, low average energy to low temperature.
In a slightly different context, certain mixtures of electromagnetic radiation can be assigned a temperature (“radiation temperature”), a single parameter that completely defines the basic properties of the radiation (more precisely, its spectrum). It corresponds to the thermal radiation emitted by a hot body with precisely that temperature.
In physics, temperature is measured in Kelvin, in everyday life, depending on the country, in Fahrenheit or Celsius.
templates
When measuring gravitational waves, researchers use so-called templates in order to separate real gravitational wave signals from background noise. For this purpose, they calculate the waveform of gravitational waves of certain different origins, such as coalescing black holes. Knowledge of the signals’ shapes facilitates their identification in the detector data.
test particles
In the context of gravity: body whose mass is so small, that it can be used to probe the gravitational influences of their bodies, as its own gravitational field is too small to affect or change the situation in any significant way.
Analogously, in electromagnetism: small, charged body with so little charge that it can be used to explore the electromagnetic influence of other bodies without its presence affecting or changing the situation in any significant way.
tests of general relativity, classical
The first two tests of general relativity were the comparison between prediction and observation for the perihelion advance of the planet Mercury and for the deflection of light near the Sun. In 1959, measurements of the gravitational redshift provided an additional test. All three effects in questions were predicted by Einstein, and these and subsequent measurements are known as the classical tests of general relativity. Measurements of the Shapiro time delay are sometimes called the “fourth test of general relativity”.
More information about the deflection of light can be found in the spotlight text The gravitational deflection of light, while the connection of this effect with one of the fundamental principles of general relativity is explored in The equivalence principle and the deflection of light.
Synonyms: classical tests of general relativity
thermal energy
The energy contained in the disordered motion of a body’s constituents – for instance, the energy of the disorderly motion of the atoms or molecules of a gas, or their oscillation in a solid body. If one increases a body’s thermal energy, one also raises its temperature.
thermal motion
What we call heat in everday life corresponds to disordered motion of the microscopically small constituents of matter (say, atoms or molecules) – one example being the chaotic dance of the molecules making up a gas, another the oscillation of the molecules forming a solid body. This disordered motion is called thermal motion, and its average energy defines a system’s temperature (cf. the preceeding entry on thermal energy).
thermal radiation
In a narrow sense: synonym for infrared radiation.
In a more general sense: The electromagnetic radiation emitted by every body with non-zero temperature due to the laws of thermodynamics. The properties of this radiation (in particular: its spectrum) depend on the body’s temperature – in the simplest case, that of what is called a blackbody, they even depend on nothing but the temperature and some universal constants.
For everyday temperatures, such as those of a hotplate, thermal radiation is emitted mainly in the form of infrared radiation. At higher temperatures, significant amounts of visible light are emitted, as well: a hotplate that is very hot indeed looks dark red or even light red; molten metal looks yellow or even white. In more extreme situations, thermal radiation can have energies that are even higher – for instance, the gases in the accretion discs of black holes are so hot that they emit great amounts of thermal radiation in the x-ray region.
thermodynamic equilibrium
A physical system is in thermodynamic equilibrium if its energy is distributed evenly among all the different ways in which its components can move or vibrate – what physicists call the system’s “degrees of freedom” – and there is no flow of energy within or at the boundaries of the system. The average energy per degree of freedom is a direct measure of the system’s temperature.
For example, for a gas, the kinetic energy of all its many particles is, on average, the same.
The totality of all electromagnetic fields is a physical system as well. More information about how thermal equilibrium of a hot body and the electromagnetic fields leads to the emission of thermal radiation can be found in the spotlight text Heat that meets the eye.
The situation is slightly more complicated in systems that allows transmutations – for instance a system consisting of particles of species A and particles of another species B, where A-particles can change into B-particles and the other way around, For such a system, equilibrium at a certain temperature implies definite values for the relative abundances of the different particle species – how many particles of species A there should be, on average, for each particle of another species B. Such equilibria are of great importance for the physics of the early universe, as described by the big bang models.
third-generation gravitational-wave detector
Third-generation gravitational-wave detectors are supposed to measure gravitational waves with higher sensitivity than current detectors such as Advanced LIGO or Advanced Virgo. Examples for such projects are the Einstein telescope and Cosmic Explorer. More information is available in our related spotlight article: Third-generation gravitational-wave detectors.
tidal effects
Idealized situations apart, the gravitational influences acting on an object depend on the object’s position. Take two small objects in the neighbourhood of a massive body: If one of them is closer to the massive body, it will be subject to a stronger gravitational pull. All effects that can be traced back to this variation of gravitational influences from location to location are called tidal effects.
Whenever gravitation is regarded as a force (notably in Newton’s theory of gravity), tidal effects are caused by minute force differences – differences in the strength and direction of the gravitational force at one point in space, as compared to a neighbouring point. These force differences, in turn, are called tidal forces.
The best-known example for tidal effects is the one responsible for their name: High tide and low tide at the sea-shore are caused by position-dependent variations of the gravitational force – very roughly speaking, the oceans on the side of the earth facing the moon are pulled towards that heavenly body more strongly than the solid globe of the earth, and that globe in turn feels a stronger pull than the oceans on the side facing away from the moon.
In the context of general relativity, tidal forces are especially interesting where singularities are concerned – in fact, the theory predicts that regions near a singularity are dominated by very strong and rapidly changing tidal forces (for more information on this, see the spotlight text Of singularities and breadmaking.
Synonyms: tidal forces
time
It is a fact of life that not all events in our universe happen concurrently – instead, there is a certain order. Defining a time coordinate or defining time, the way physicists do it, is to define a prescription to associate with each event a number so as to reflect that order – if event B happens after event A, then the number associated with B should be larger than that associated with A. The first step of this definition is to construct a clock: Choose a simple process that repeats regularly. (What is “regular”? Luckily, in our universe, all elementary processes such as a swinging pendulum, the oscillations of atoms or of electronic circuits lead to the same concept of regularity.) As a second step, install a counter: A mechanism that, with every repetition of the chosen process, raises the count by one.
With this definition, one can at least assign a time (the numerical value of the counter) to events happening at location of the clock. For events at different locations, an additional definition is necessary: One needs to define simultaneity. After all, the statement that some far-away event A happens at 12 o’clock is the same as saying that event A and “our clock counter shows 12:00:00” are simultaneous. The how and why of defining simultaneity – a centre-piece of Einstein’s special theory of relativity – are described in the spotlight topic Defining “now”.
With all these preparations, physicists can, in principle, assign a time coordinate value (“a time”) to any possible events, and describes how fast or how slow processes happen, compared to that time coordinate.
time dilation
In special relativity: From the point of view of an observer (more precisely: an inertial observer), a moving clock goes slower than an identically built clock at rest. All other processes moving alongside the clock (for instance: everything happening aboard a rocket speeding by) are slowed down in an identical fashion.
Time dilation can be mutual: When two inertial observers speed past each other, each will find that the other’s clocks go slower.Some aspects of this unfamiliar mutuality are explored in the spotlight topic The dialectic of relativity; a geometric analogy is presented in Time dilation on the road.
In general relativity, there is the phenomenon of gravitational time dilation: Roughly speaking, clocks in the vicinity of a mass or other source of gravity run more slowly than clocks which are farther away. This phenomenon is closely related to the gravitational redshift.
torus
A torus (pl. tori) is a surface shaped like that of a donut or bagel.
It is possible to define analogous geometric objects, all of them finite in extent and closed in upon themselves, with more dimensions than two. These are also known as tori; whenever it is necessary to indicate such an object’s dimensionality, one can simply add a qualifier to the name: The donut surface is a two-torus (two-dimensional), its three-dimensional analogue is a three-torus, and so on.
transversal
A wave is called transversal if the effects associated with it (the electric forces associated with an electromagnetic wave, or the space distortions caused by a gravitational wave) act only in directions perpendicular to the wave’s direction of propagation. For gravitational waves, some more information about this property can be found in the spotlight text The wave nature of gravitational waves.
Synonyms: transversality
triangle
In a plane and other flat space: Geometrical object consisting of three points (“vertices”) with three connecting straight lines.
The definition can be made more general, in a way that applies to curved spaces, as well: A geometric object consisting of three points (“vertices”) connected by three segments of geodesics.
tritium
Variety of hydrogen in which the atomic nucleus contains two neutrons and a proton. In ordinary hydrogen, the nucleus consists of a single proton; in heavy hydrogen (deuterium) there is one additional neutron.
In the context of general relativity, tritium is of interest as one of the species of light atomic nuclei that formed in the early universe during Big Bang Nucleosynthesis.
tunnel effect
A quantum mechanical phenomenon that can be pictured as follows. Imagine a ball rolling towards a hill:
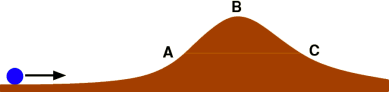
Leaving quantum effects aside (in other words, in classical physics), we expect that what happens depends on the ball’s energy: If the ball moves fast enough (i.e. has sufficient energy), it will climb the hill, pass the peak at B and roll down on the other side. If the ball is too slow, it will reach some maximum height and then begin to roll back down without having passed B.
In the analogous situation for a quantum particle, there is another possibility. Even an incoming particle with enough energy to climb to the height A, but not to pass the peak B, can appear on the right-hand side of the hill at point C and continue onwards. Such a transition is called tunneling – it is as if the particle had taken a secret tunnel from A to C to avoid the forbidden peak around B and arrive directly at C.
More generally, tunneling describes any transition from a state A to a state C that a quantum system can make, but that is forbidden to analogous systems in classical physics, since there, getting from A to C would only be possible by passing through a forbidden state B.
Synonyms: tunnelling, tunneling
twin effect
Effect of special relativity, variant of the time dilation effect: A twin that uses a high-powered rocket to travel in space with a speed near that of light before returning ages less than his twin sibling that has remained on Earth.
The question why this is sometimes thought to be a paradox, while it really isn’t, is explored in the spotlight topic The case of the travelling twins; a geometric analogy that is not about time, but about distance, is developed in Twins on the road.
Synonyms: twin paradox




