The wave nature of simple gravitational waves
A closer look at the way that simple gravitational waves propagate through space with time
An article by Markus Pössel
What makes a gravitational wave a wave? The standard illustrations (and animations) show the influence of a gravitational wave on a collection of particles floating in space:
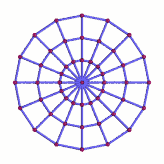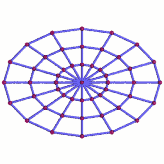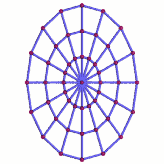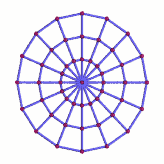
Gravitational wave
In this animation, the red spheres are the free particles, and we have connected them with blue lines. While the resulting impression is that of a solid grid, the blue connections are only there for your visual convenience, to help you keep track of which particle is adjacent to which other particle. In particular, they are not any kind of solid or elastic link between the particles.
The influence of the gravitational waves shows itself in the way that the distances between the particles are changing over time. In the simple example above, there are two distinct possibilities: Sometimes, the gravitational wave stretches all vertical distances between particles and, at the same time, squeezes all horizontal distances. At other times, all horizontal distances are stretched while all vertical distances are squeezed. As always in such illustrations, the stretching has been exaggerated to make it visible to the naked eye – in reality, the stretching is more than a trillion billion times less pronounced.
In order to produce this pattern, the gravitational wave must be travelling at a right angle to the image plane, either directly towards or directly away from the viewer.
Simple sine oscillations
If you took two particles and made a plot of their distance changing with time, the result would be a regular succession of maxima and minima – for the above animation, it would look something like this:
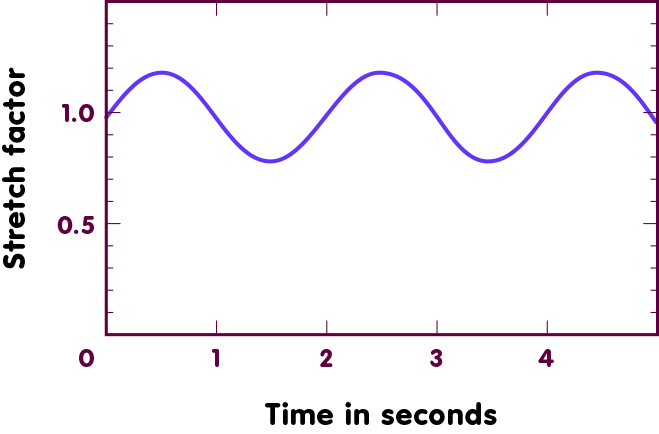
The “stretch factor” is the factor by which the distance is either stretched (when the factor is greater than one) or squeezed (when it is smaller than one). The exact timing of the animation might differ from the one charted here, depending on your computer and browser.
In this particularly simple case, the physical quantity that is used to describe gravitational waves (namely the change in the square of the distance between adjacent particles), is a simple sine function. Correspondingly, these waves are called sine waves.
However, what we have seen in the animation above (and also in other standard animations such as in The rhythm of geometry, part of our introduction Elementary Einstein) are, strictly speaking, not gravitational waves, but merely “gravitational oscillations” – periodic changes in distance for particles in one particular plane. A wave is more than that – it is an oscillatory pattern that propagates through space.
From oscillation to wave
In the case of our simple gravitational wave, this means taking the third space dimension into account. The animation above shows a single plane. But parallel to that plane, above it as well as below it, are other planes on which we can place particles. Distances between particles that reside in these planes experience exactly the same kind of distortion as in our particular example – with one crucial difference: timing.
For instance, at the moment when particle distances in a particular plane are maximally stretched in the vertical direction, vertical distances in the plane directly behind are in a slightly earlier stage where the stretching has not quite yet reached its maximal value. More generally: If plane A is located in front of plane B, it will lag behind plane B in going through the oscillation. Here is an animation showing what is happening in the different planes:

Gravitational wave traveling towards you through different planes
The time-lag between one plane and the next is what generates the traveling wave pattern. In the animation, you can see how the bulges and dents – maximal and minimal stretching in a given direction – travel towards you.
If we change our point of view so as to view the planes edge-on, you can see more clearly that the wave consists of a pattern of stretching and squeezing with maxima and minima moving through space at a constant speed, like the crests and troughs of a water wave:
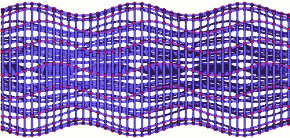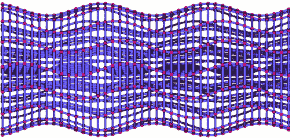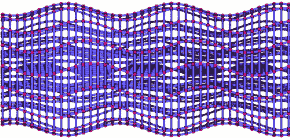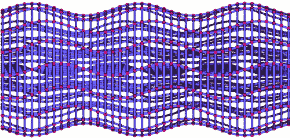
Gravitational wave sideways detail
The animation also illustrates a more general property of simple gravitational waves. As you can see, in the direction of the wave’s propagation, the separation between particles does not change. In this particular animation, the wave travels from right to left, and in mapping the change in particle distances caused by the gravitational wave, we only have to shift particles upward or downward, toward us or away from us, but not sideways. Simple gravitational waves only squeeze and stretch space in directions perpendicular to the direction of their propagation. In the language of physics, such waves are called transversal.
In a snapshot of that wave propagation, you can recognize the earlier example for the time lag – the plane that, at present, experiences maximal stretching in the vertical direction, and the neighbouring planes that just recently were, or soon will be, maximally stretched:
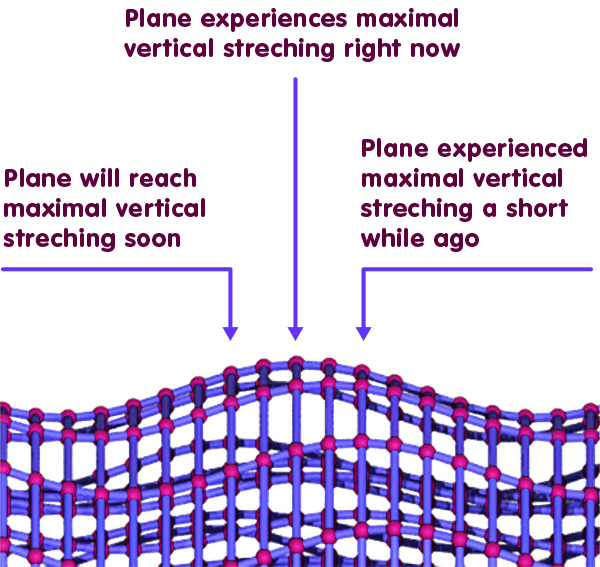
Gravitational wave in detail
Of course, even if we restrict ourselves to simple sine-like waves, the exact appearance of the three-dimensional travelling pattern will depend on the details of their oscillation (on what physicists call the wave’s “polarization”). Here is an example different from the above – an “elliptically polarized” wave which looks somewhat like a rotating helix as the pattern travels through space:

Gravitational wave – elliptically polarized
But whatever the details of the oscillation – we always have a simple pattern propagating through space, and that is why we call this phenomenon not “gravitational oscillations”, but gravitational waves.
Further Information
For background information on gravitational waves, check out Elementary Einstein, in particular the chapter Gravitational waves.
Related Spotlight topics on Einstein Online can be found in the section Gravitational waves.
Colophon
is the managing scientist at Haus der Astronomie, the Center for Astronomy Education and Outreach in Heidelberg, and senior outreach scientist at the Max Planck Institute for Astronomy. He initiated Einstein Online.
Citation
Cite this article as:
Markus Pössel, “The wave nature of simple gravitational waves” in: Einstein Online Band 02 (2006), 02-1008










