Of singularities and breadmaking
About some characteristic properties of spacetime near singularities – and the violent deformations they cause for any object unlucky enough to approach a singularity
An article by David Garfinkle
The gravitational collapse of massive stars can lead to the formation of a black hole: a region of spacetime where gravity is so strong that nothing that has ventured inside can ever escape – not even light. This means that we cannot see the interior of a black hole. But, nonetheless, we can ask what general relativity, the theory on which our description of black holes is based, has to say about black hole interiors. One important part of the answer might surprise you: What happens to an object that has fallen into a black hole bears a certain similarity to what happens to dough in the process of making bread!
An end to free fall
One direct consequence of general relativity is that, inside the black hole, the collapse of the star does not halt. Nothing can travel faster than light, and inside the black hole, even light is pulled ever further inward by gravity. Thus, inside a black hole, even in order to simply remain where you are (to say nothing about moving outwards and escaping!), you would have to travel faster than light.
Thus, there is no standing still, and a collapsing star that has formed a black hole will continue its collapse ever further. In the process of this collapse, the density of the stellar material will increase all the way to infinity, or at least to the mind-bogglingly huge density at which quantum gravity effects become important. At infinite density, we have reached what is called the black hole singularity.
At the singularity, any observer unlucky enough to have fallen into a black hole will cease to exist. In fact, this notion of infalling observers simply ceasing to exist is the usual definition of a singularity (more information about which can be found in the spotlight text Spacetime singularities). It is used in a number of famous theorems called singularity theorems which show that, in the context of Einstein’s general theory of relativity, such singularities must necessarily occur, for instance in certain types of stellar collapse.
Approaching the singularity
However, just knowing that freely falling observers cease to exist (or, using the geometric language of general relativity, that “their world-lines end”) does not tell us much. We would like to know more about the nature of these singularities.
One thing that we know about gravity is that the gravitational field of an object tends to compress that object – gravity is universally attractive, and its effect is to pull the different portions of an object closer together. In turn, as an object is compressed, its gravitational field becomes stronger: For instance, the gravitational pull on an object near the surface of the sun is about ten thousand times weaker than the pull on an object near the surface of a White dwarf star with the same mass but with a mere one hundredth of the sun’s radius. We might guess that a singularity is simply that process continued to its ultimate limit, with ever larger density producing an ever larger gravitational field, which in turn leads to ever larger density, and so on until finally both the density and the gravitational field become infinite.
That is indeed how gravitational collapse starts, but it is not how it ends. The reason is that, in the language of mathematics, Einstein’s equations governing gravity are nonlinear. Translated from mathematics to physics, this means that gravity itself has a gravitational effect – gravity itself produces further gravity! (More information about this can be found in the spotlight text The gravity of gravity.)
Thus, once gravity gets strong enough, the gravitational field itself will make a significant contribution as a source of further gravity, giving rise to an even stronger gravitational field, which in turn gives rise to an even stronger gravitational field, and so on until, at the singularity, gravity is infinitely strong. Remarkably, as one approaches the singularity, it is this gravitation of gravity, rather than the gravitation of matter, that is the most important effect – or, as it is sometimes said, near a singularity matter doesn’t matter.
This means that physicists interested in the general nature of singularities do not need to worry about the properties of the matter that began the gravitational collapse and can even study simplified models with no matter at all, so-called vacuum solutions of Einsteins field equations. That singularities have this property was first theorized by the Soviet physicists Vladimir Belinskii, Isaak Khalatnikov and Evgeny Lifshitz (collectively known as BKL) back in the 1970s.
The three also theorized that as a singularity forms, the gravitational field is so rapidly changing in time that the essential properties of singularities can be understood by considering only the dependence of the gravitational field on time and neglecting its dependence on space. These two notions, that near a singularity only the gravitational field itself, and only its dependence on time are important, became known as the BKL conjecture.
Tidal deformation
So if matter doesn’t matter, what does matter as you approach the singularity? The short answer is: two aspects of the gravitation of gravity called “shear” and “spatial curvature.”
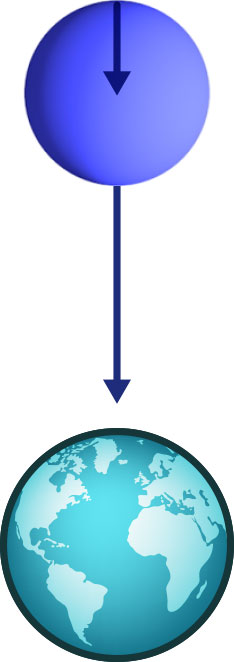
Shear simply means that an object falling towards the singularity gets compressed or stretched by a different amount in different directions. This is related to the aspect of gravity known as the tidal force. For instance, a giant blob of water or a cloud of dust particles falling towards the earth will be stretched in the vertical direction and compressed in the horizontal direction, as can be seen in the following animation:
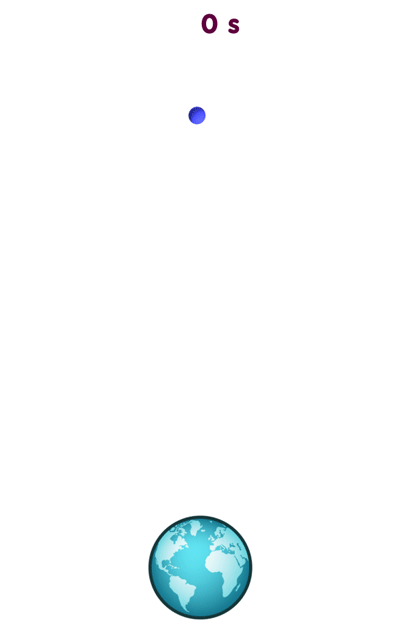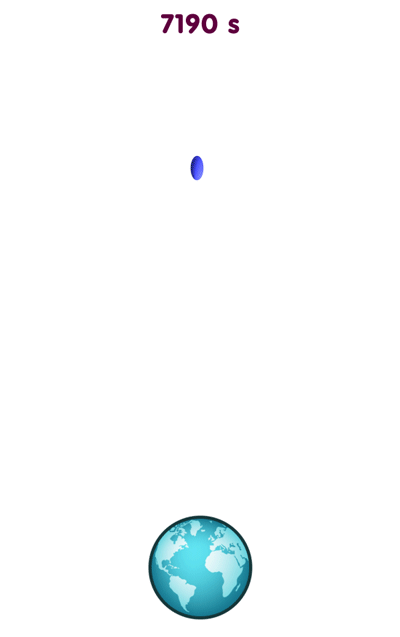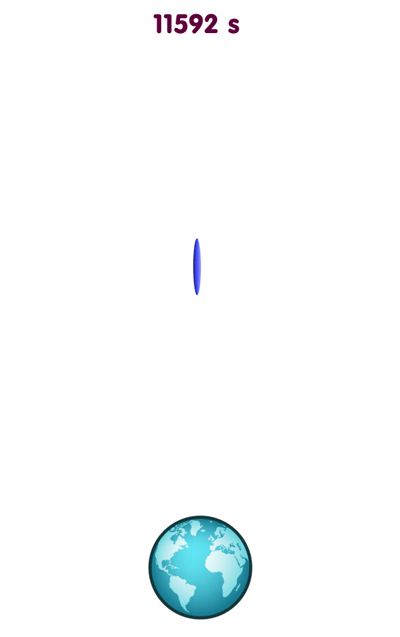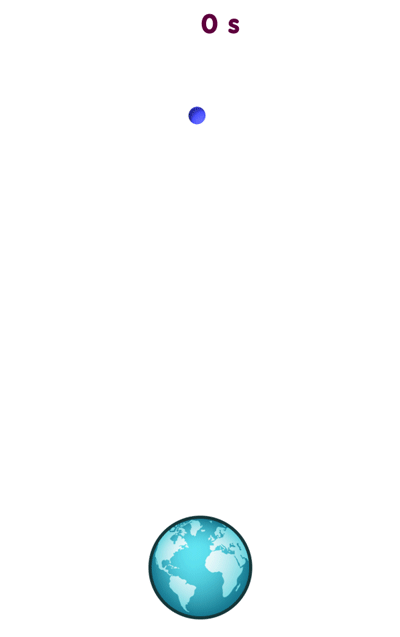
[Image uses data from NASA’s Visible Earth]
The nature of the deformation is easier to see if you do not have to follow the object’s motion with your eyes, so here is a view of the same falling object, captured by a camera falling alongside:

The vertical stretching comes about because the strength of gravitational attraction decreases with distance. Thus, the bottom of the object, being slightly closer to the Earth than the top of the object, experiences a slightly stronger pull. In the following image, which shows a somewhat larger object being attracted by the earth, the length of the arrows represent the strengths of gravitational attraction:
[Image uses data from NASA’s Visible Earth]
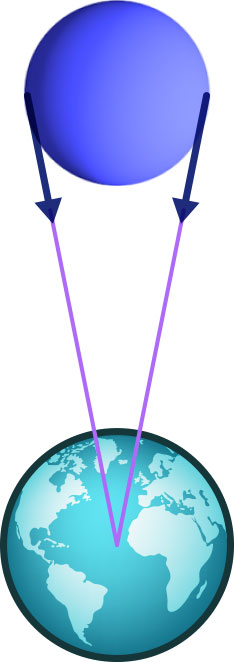
[Image uses data from NASA’s Visible Earth]
Shear, curvature and singularities
In the same way as an object falling towards the earth, an object falling towards the singularity will be compressed in two of the three spatial directions, and stretched in the third. Near the earth, the shear is comparatively weak, and small, solid objects such as spacecraft can easily resist deformation. But as the singularity is approached, the shear becomes ever stronger. Eventually, it becomes stronger than any of the forces which make solid objects keep their shape, and any object approaching the singularity is torn apart.
In addition – a prime example of gravity begetting further gravity – the shear gives rise to a curvature of space which in turn gives rise to a very rapid change in the directions of the shear. Thus an object that was just now being stretched in the vertical direction (the direction of the object’s fall) and compressed in the horizontal directions…
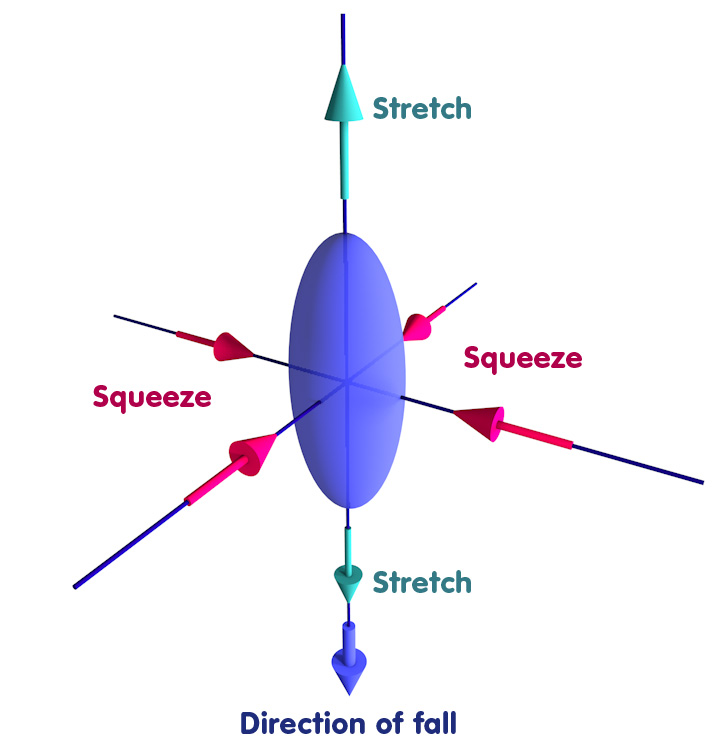
…will suddenly be compressed in the vertical direction and one of the horizontal directions while being stretched in the other horizontal direction:
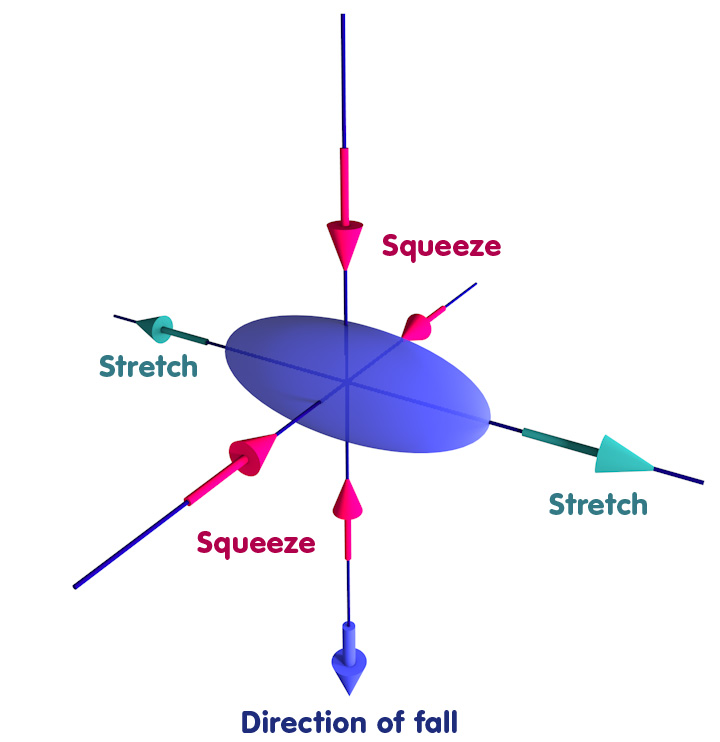
The result is violent stretching and squeezing similar to what is experienced by dough in a bread making machine. The following animation shows a glimpse of what an object would go through as it nears the singularity:

[Animation using data from a simulation by D. Garfinkle]
Given the similarity to bread-making, the technical term that physicists have coined for the sequence of stretching and squeezing that occurs as the sigularity is approached is “mixmaster dynamics”, named after the Mixmaster, a particular model of mixer used among other thing for the preparation of bread dough.
Using computers to simulate singularities
Though the essential insights into the nature of singularities date back to Belinskii, Khalatnikov and Lifshitz in the 1970s, it is only in recent years that these insights have been shown to be correct. In this, numerical relativity – the use of computer simulations to explore Einstein’s theories of relativity – has played a crucial role.
In numerical relativity, computers are used to simulate the properties of model universes which are taken to be governed by the laws Einstein laid down for his theory of general relativity. In the particular simulations that are of interest here, information on a system in the early stages of gravitational collapse is given to the computer. The computer then makes use of Einstein’s equations to find how the system develops in time. Sure enough, in the simulation, it is the gravitational field and its time dependence that eventually becomes the dominant factor. Also, the computer simulation produces the same sequence of stretching and squeezing that BKL predicted – in fact, the animation above is based on data from one such simulation.
Such computer simulations of singularities are an ongoing topic of research and there is still plenty of work to be done on this subject. In particular, so far, only the collapse of certain types of matter has been simulated. More types of matter need to be checked to see whether the properties of matter indeed become negligible as the singularity is approached. Simulating singularities is quite a challenge – it requires both efficient simulation codes and impressive computing power. A more detailed look at the process of singularity formation will require yet more accurate computer simulations run on yet more powerful computers.
As a reward, we can expect to obtain even more interesting insights into the nature of singularities. For instance, there is a conjecture, due to the Canadian physicists Werner Israel and Eric Poisson, that in gravitational collapse to form a black hole only part of the singularity is of the BKL type, with the rest being a milder type of singularity with a weaker tidal force. To provide a reliable checks of this Israel-Poisson conjecture is one of the challenges to be taken on by future simulations.
The quantum nature of singularities
The mathematics of general relativity indicate an infinite sequence of the rapid changes in direction of the shear as all physical quantities approach infinity at the singularity. However, only a fairly small number of these changes occur before the spacetime curvature becomes so enormous that we reach the limits of general relativity. When curvature becomes so great, we can no longer ignore quantum effects, and the proper theory to describe what happens would be a theory of quantum gravity. Thus the ultimate answer to the question of the nature of singularities requires a quantum theory of gravity. And this, in turn means that we might need to be patient. Though much work is being done to develop a quantum theory of gravity, this work is not yet to the point where it can be used to determine the quantum nature of singularities.
Further Information
Relativistic background information for this Spotlight topic can be found in Elementary Einstein, in particular in the chapter General relativity.
Further related Spotlights on relativity can be found in the category General relativity.
The earth surface data used in some of the images was kindly provided by NASA’s Visible Earth.
Colophon
David Garfinkle is a professor of physics at Oakland University with a focus on numerical relativity.
Citation
Cite this article as:
David Garfinkle, “Of singularities and breadmaking” in: Einstein Online Band 03 (2007), 03-1014










