Time dilation on the road

How you can picture the relativity of simultaneity and time dilation, using a simple geometric analogy

An article by Markus Pössel

For a number of relativistic phenomena, there are helpful geometric analogies. They transplant space-time-phenomena to the more familiar arena of space geometry. Most people might not be familiar with space-time-lines and -projections, but they do know, for instance, how it looks when two lines in space intersect. This spotlight topic is about one such analogy, designed to make more accessible some of the properties of relativistic time dilation and the relativity of simultaneity.

Same-level-ness along the road

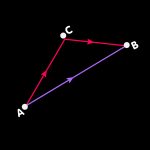
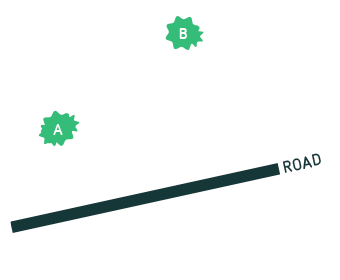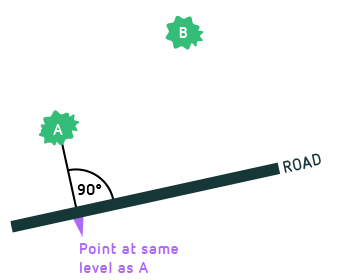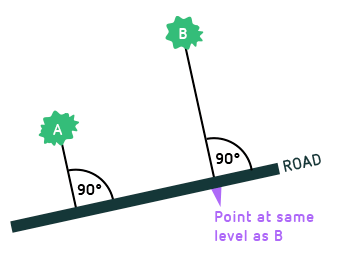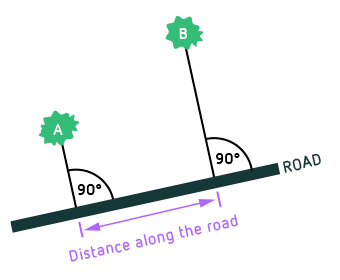
Imagine a hiker moving along a straight road. For the hiker, her road is a natural reference line in the landscape. For instance, she can define what it means when two objects are “at the same level” relative to the road. For two objects at the same level, there is a point on the road where one of the following statements is true: If the hiker is facing forward, then to see those objects, she either needs to turn her head 90 degrees to one side (upon which she will see the two objects in question lined up). Or she needs to turn her head once 90 degrees to one side, seeing one object, and then to the opposite side to see the second object. If either of those statements is true, the two objects (and, at that point on the road, the hiker) are at the same level. To give some examples, the following figure shows the road and several trees, as seen from above:

In the language of basic geometry, the definition is more concise: Two objects are “at the same level (with respect to a given road)” if the straight line connecting them intersects the road at a right angle.

Two hikers compare their observations

Looking at two hikers on different straight roads, it soon becomes clear that “at the same level” has a different meaning for each of them. This is illustrated in the following figure: For the hiker on road 1 (light brown), tree A and tree B are at the same level, but not the trees B and C. For the hiker on road 2, it is the other way around:

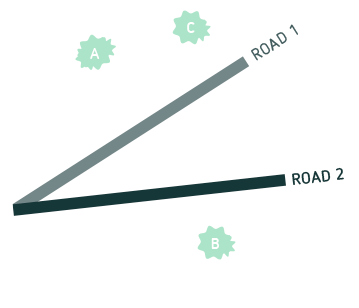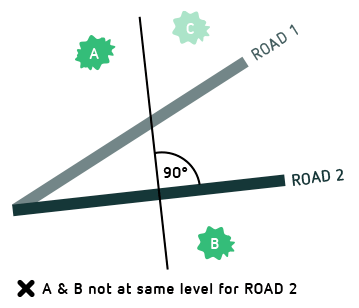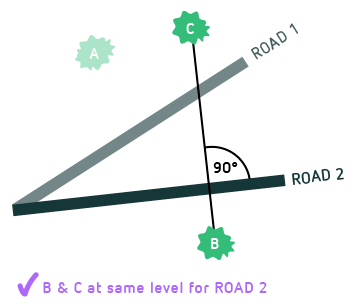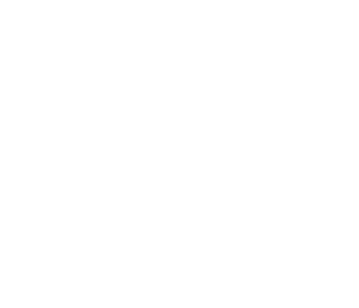
Being at the same level (let’s call it “levelness”) is relative – whether or not two landmarks are at the same level depends on the road the hiker is taking.

The analogy with special relativity

As for the analogy with special relativity: there, we are not dealing with the two spatial dimensions of a landscape seen from above, but with one time and several space dimensions. Instead of hikers on different roads, we examine observers in relative motion (to be precise: inertial observers), with a larger angle between two roads corresponding to a higher relative speed of two observers. Each hiker defines levelness – a criterion to decide which landmarks are at the same level. Each relativistic observer defines simultaneity – a criterion to decide whether or not two events happen at the same time. Levelness is relative, as clearly shown in the figure above. So is simultaneity, in special relativity: In deciding which events are simultaneous, different observers will reach different conclusions.

So far, so analogous. In fact, the analogy can be made much more precise. Physicists know of ways to represent spacetime, observers and events graphically, resulting in so-called spacetime diagrams. In those diagrams, the reference frames of the different observers look very similar to the two different roads pictured above, and from this, the relativity of simultaneity can be derived as directly as the relativity of levelness from the diagram above.

“Levelness” is not the only road-dependent definition each hiker can make. Another is “distance along the road”. For two objects, there is exactly one point on the hiker’s road that is at the same level as the first object, and one point at the same level as the second. The distance between those two points, measurable by the hiker without leaving the road, is the distance along the road between the two objects:

The distance along the road is a useful piece of information for the hiker: if she is right across from the first landmark, this distance tells her how far she must go until she passes the second one.

In the spacetime of special relativity, any observer can use his concept of simultaneity to measure time intervals between different events – even if those events happen far away. The recipe is simple: That observer must carry with him a clock. Simultaneously with the first event, he reads the time off his clock, and he does the same for the second event. The difference between those two times is the time interval between the two events.

Such a time interval is the analogue of the “distance along the road” we have defined for our hikers – here, the analogy is summarized in tabular form:

The relativity of distance

Next, let’s go back to looking at two hikers. In the following illustrated example, their roads intersect at an angle of 60 degrees. Imagine the hiker on path 1 marking a distance of one kilometre on her road. If the hiker on path 2 measures the distance of the endpoints of this marked-out piece of road 1, she obtains a distance-along-the-road (her own road!) of a mere 500 metres. And vice versa: if the hiker on path 2 now measures out one kilometre, the hiker on path 1 will find that the distance-along-her-road of the endpoints is merely half that value:

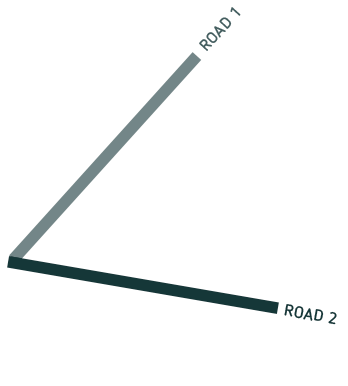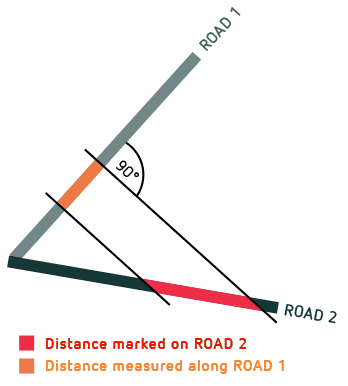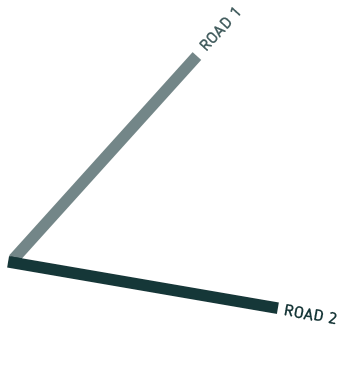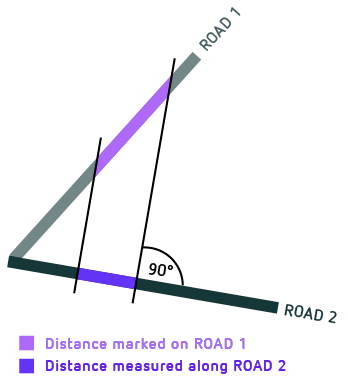
As the illustration shows, the relativity of levelness is responsible for the relativity of distances-along-the-path – for each hiker measuring a shorter distance for any interval staked out along the other path.

The relativistic analogue of this is time dilation: From the point of view of each of two observers in relative motion, the other observer’s clocks will run slower than his own. If observer 1 sees the space station of observer 2 fly by with 87 percent of light speed, he will find that for every second that passes on a clock on that space station, two seconds have passed on his own clock. Correspondingly, observer 2 considers himself to be at rest, sees the first observer’s space station zip by at 87 percent light speed, and finds that the clocks of observer 1 go much slower than his own.

At a first encounter with relativity, this state of affairs is often viewed as paradoxical – how can it be that each of the observers considers the other’s clocks to go slower than his own? In reality, it is no more paradoxical than each of the two hiker’s measuring a shorter distance-along-the-road for an interval staked out by the other. In that case, different concepts of levelness serve to resolve the apparent contradiction. For time dilation, the different concepts of simultaneity – to each observer his own – make it possible to reconcile the two observations. (Some more information on this can be found in the spotlight topic The dialectic of relativity.)

By the way: The hikers and their roads can also be helpful to understand the situation of the famous twins, one of whom takes a journey on an ultrafast spaceship and, upon her return, is markedly younger than her stay-at-home sibling – this part of the analogy is developed in the spotlight topic Twins on the road.

Further Information