General relativity / Elementary Tour part 3: A planet goes astray
The first test of general relativity concerned a situation in which Newton’s and Einstein’s theories give almost the same result – with a small but crucial difference. The scene: our cosmic backyard, the solar system. The protagonist: Mercury, the planet closest to the sun. For a lonely planet orbiting the sun, Newtonian physics (more precisely: Kepler’s laws of planetary motion, which can be derived from Newtonian mechanics) predict an elliptical orbit, with the sun in one of the focal points.
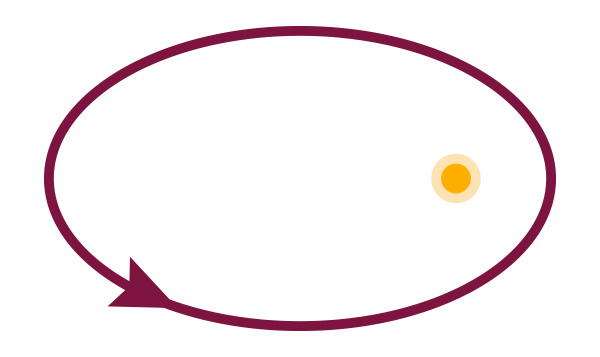
closed elliptical orbit
For the same situation, Einstein’s theory predicts a slightly different orbit: not an ellipse, but a kind of rosette. As Mercury orbits around the sun, the two points of each orbit closest to the sun and furthest away from it (in astronomical lingo: perihelion and aphelion) should ever-so-slightly shift from one orbit to the next. The following figure shows an exaggerated version of this movement:
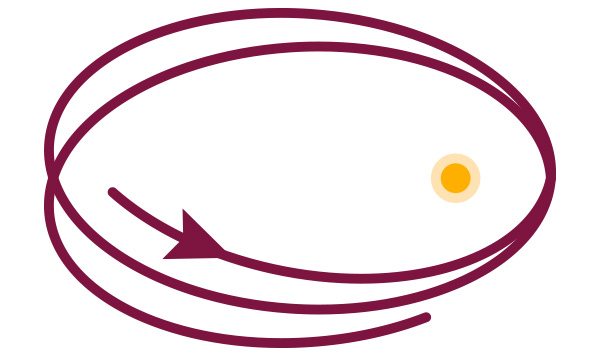
orbit with perihelion shift
In the solar system, where there’s more than one planet orbiting the sun, the situation is a bit more complicated. There, the mutual gravitational pull of the planets on each other leads to a slight shift of perihelion and aphelion points, even without Einstein’s results. However for Mercury, where the relativistic effect should be strongest, the shift that we observe is slightly larger than expected. Even when the influence of all the other planets taken into account, a slight extra contribution is left over. A simple calculation in general relativity predicts exactly that tiny additional shift. Since astronomers routinely use the perihelion as their reference point, this is called the relativistic perihelion shift (just as, among astronomers, the extra contribution, unexplained in pre-Einstein physics, was the “anomalous perihelion advance” of Mercury). While this effect is most pronounced for Mercury, more recent measurements have also confirmed it for Venus, Earth and Mars.










