The definition of “now”
Why it is necessary to define simultaneity, and how best to go about defining it.
An article by Markus Pössel
Simultaneity is something we rarely think about – we just accept it as a fact of life. However, thinking matters through, it isn’t obvious at all how one can determine whether or not two events at two different locations happen simultaneously, or not.
Clocks to go
In everyday life, our solution is simple: We carry clocks, be they watches or the clocks built into mobile phones. If I synchronize my watch with my grandfather clock at home, I then simply assume: event A which happens at my home and event B that happens at my current location occur simultaneously, say, at 12 o’clock, if the grandfather clock begins to strike 12 o’clock at the time of event A, while my own watch shows 12:00:00 at event B. However, if we measured time more precisely (alternatively: if we undertook trips with very fast space-ships) we would realize that clocks are influenced by motion. The simple fact that I and my watch move around during the day means that an ultra-precise direct comparison of it and the grandfather clock, undertaken when I have returned home for the evening, would show a minute difference – time dilation, a well-known consesquence of special relativity, will have taken its toll. Motion influences clocks – and that means that, for a fundamental definition of simultaneity, one should not rely on simply carrying clocks around.
Using light to synchronize clocks
A plausible next step is to use light to transmit information. For instance, I can attempt to read the time off two clocks with the help of a special camera, fixing what they show onto a photographic plate:

If, on such a photograph, the two clocks are shown exactly in the 12 o’clock position – does that mean they are perfectly synchonized – that they show the same time, simultaneously? On the contrary, if they look the same on the photograph, I can be sure that they do not run synchronously. After all, the light that carries the information about the clock on the right to the camera on the left needs a tiny amount of time to do so. If it arrives at the camera simultaneously with the light showing “12 o’clock” on the left clock, then it must have left the right clock a bit earlier, in other words: the right clock must have struck noon a bit earlier than the left.
To compensate for this effect, there is a simple solution: Place a special camera exactly in the middle between the two clocks, and have the camera combine what the two clocks show into a single picture:
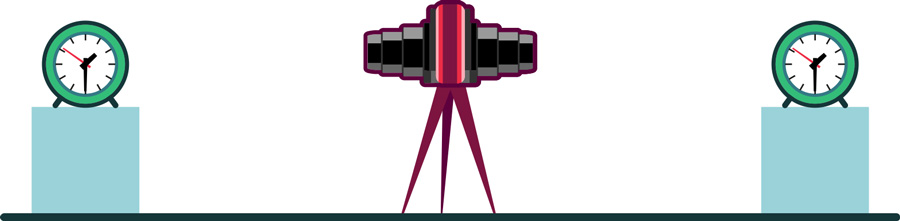
In this situation, the light from both clocks needs exactly the same time to reach the camera in the middle. If the two clocks appear to show the same on the photograph, that means they did show the same at the time the light began carrying that information to the middle.
Or does it? This argument only works if the light travelling from the left clock to the middle was exactly as fast as the light travelling from the right. How do we know that light speed is the same in all directions? One might think that this should be an easy thing to test by direct measurement. Not so: In order to measure how much time light takes to travel from a location A to another location B, one needs two clocks, one at A, one at B. With these clocks, I measure the time when the light has left A, and the time when it has reached B. But for the time difference to make sense, and to tell me how long the light has travelled, these two clocks need to be synchronized in the first place – they need to show the same time, simultaneously. And that’s where we come full circle – after all, we’re still trying to find out how to determine simultaneity in the first place! The only light speed we can measure without that definition is one closed paths, which end at the same location they begin, so we can measure the light’s run-time on a single clock. For such closed paths, we find that, indeed, light moves with the same constant speed, regardless of the paths’ orientation.
Simultaneity: A matter of definition
To break the vicious circle, one need but realize that simultaneity is not something that is given, it is something that needs to be defined. And it makes sense to use the properties of light for that definition After all, if light always runs at the same average speed on closed paths, it makes sense to define simultaneity in a way that light also moves with constant speed from A to B. This definition has the added advantage of reflecting what all other physics experiments would tell us – that there is no preferred direction in space. Once we have taken this step, we can use the definition of simultaneity developed above: two events are simultaneous if and only if they can be seen on the same photograph, taken with a double camera placed exactly in the middle between their locations.
Einstein’s postulate of the constancy of the speed of light, the basis of his special theory of relativity thus has a number of facets: “The speed of light is the same for any observer (more precisely: for any inertial observer)”: Part of this can be tested experimentally, namely the two consequences that the speed of light on any round trip must be constant, and that the speed of light is independent of the motion of the source. But another aspect is purely coventional – that the speed of light moving from A to B is constant implies a very specific definition of simultaneity – the definition I have introduced above.
Using the postulates of special relativity, one can show that simultaneity, defined in this way, depends on the chosen frame of reference. Notably , with two double-cameras which are moving relative to each other, observers will record different results for which events are simultaneous and which aren’t. This has direct consequences on how observers in relative motion measure lengths and time intervals. In special relativity, such measurements, too, depend on the movement of the observer. In this way, the discovery that simultaneity is not something given, but something that needs to be defined, leads to special relativity’s most revolutionary new predictions.
Further Information
The definitions given here form the basis of special relativity, information about which can be found in the chapter Special relativity of Elementary Einstein.
Related spotlight topics on Einstein-Online can be found in the section Special relativity.
Colophon
is the managing scientist at Haus der Astronomie, the Center for Astronomy Education and Outreach in Heidelberg, and senior outreach scientist at the Max Planck Institute for Astronomy. He initiated Einstein Online.
Citation
Cite this article as:
Markus Pössel, “The definition of “now”” in: Einstein Online Band 04 (2010), 01-1001









