Avoiding the big bang

The collapsing and then re-expanding quantum universe that loop quantum gravity offers as a replacement of the standard big bang models

An article by Martin Bojowald

So far, there are no observations, astrophysical or otherwise, that would lead scientists to question the validity of Einstein’s general theory of relativity. Nonetheless, physicists know that the theory is incomplete: According to the so-called singularity theorems of Hawking, Penrose and others, the theory contains the seeds of its own destruction: If, for example, we describe the evolution of the universe with the help of the big bang models and follow that evolution back in time, we see an ever denser cosmos, and the space surrounding us today finally contracts to a single point of infinite density and infinitely strong gravity. There is no place for such infinities (called “singularities”) in a proper mathematical description of the universe, and at that point, Einstein’s equations – the basis for predicting the evolution of the cosmos – collapse as well. General relativity, this tells us, is necessarily incomplete. Its equations cannot describe the big bang singularity itself.

An infinitely old universe

There has long been hope that these limitations can be overcome within a theory of quantum gravity, a theory that unifies general relativity and the concepts of quantum theory. These hopes have recently taken on a more concrete shape, with the help of what is called loop quantum gravity, and its applications to cosmology. In the loop quantum models, the big bang universe whose beginning is haunted by infinities, as pictured here…

Expanding universe; arrow of time

…turns out to be a universe with a history reaching far beyond the big bang – a universe that, initially, was in a state of collapse, reaches zero extension at the point where general relativity predicts the big bang singularity, and, afterwards, expanded in perfect harmony with the predictions of the regular big bang models:

Quantum gravity: collapsing and re-expanding universe; arrow of time

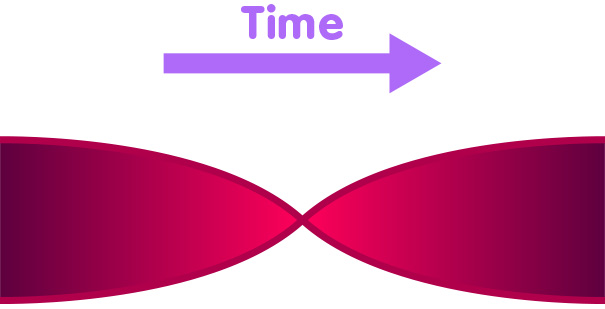
One can imagine this evolution as that of a party balloon loosing air. Normally, it would simply collapse and crumple up, but if you imagine that the different parts of its skin can pass through each other, the momentum gained in the collapse would lead to a re-inflation of the balloon, which would then be turned inside out.

Quantum properties near the big bang

The only reason this combination of collapse and expansion is possible is that as soon as the length-scales in the universe become microscopic, it enters a regime where the quantum properties of space and time – as described by loop quantum gravity – become important. In the following image, this is represented by the looking glass showing the discrete, lumpy structure of collapse and expansion near the middle:

Quantum gravity: collapsing and re-expanding universe; arrow of time; looking glass showing quantum region

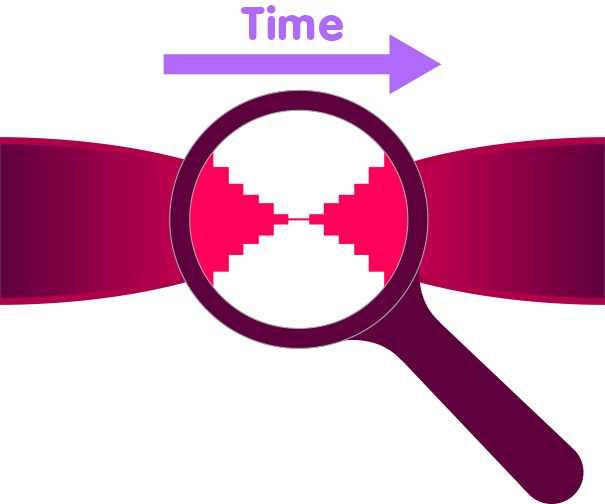
The quantum equations of the loop models show how the universe evolves into the region of extreme compression and then enters the phase of expansion that has lasted until the present day. In addition, the theory predicts that, at the turning point, space literally turns inside-out (as in the example of the party balloon) or, as mathematicians would say, changes its orientation.

Further Information

For the basic concepts of relativity of interest for this spotlight topic, check out Elementary Einstein, in particular the chapters Relativity and the quantum and Cosmology.

Some more information about how the loop models deal with the extreme physical conditions near the turning point can be found in the spotlight topic Taming infinities with loops. Related Spotlights on relativity on Einstein-Online can be found in the sections Relativity and the quantum and Cosmology.

Colophon

Martin Bojowald

is a physics professor at Pennsylvania State University with a research focus on cosmological applications of loop quantum gravity.

Citation

Cite this article as:
Martin Bojowald, “Avoiding the big bang” in: Einstein Online Band 04 (2010), 01-1023

Definitioner

time

It is a fact of life that not all events in our universe happen concurrently - instead, there is a certain order. Defining a time coordinate or defining time, the way physicists do it, is to define a prescription to associate with each event a number so as to reflect that order - if event B happens after event A, then the number associated with B should be larger than that associated with A. The first step of this definition is to construct a clock: Choose a simple process that repeats regularly. (What is "regular"? Luckily, in our universe, all elementary processes such as a swinging pendulum, the oscillations of atoms or of electronic circuits lead to the same concept of regularity.) As a second step, install a counter: A mechanism that, with every repetition of the chosen process, raises the count by one. With this definition, one can at least assign a time (the numerical value of the counter) to events happening at location of the clock. For events at different locations, an additional definition is necessary: One needs to define simultaneity. After all, the statement that some far-away event A happens at 12 o'clock is the same as saying that event A and "our clock counter shows 12:00:00" are simultaneous. The how and why of defining simultaneity - a centre-piece of Einstein's special theory of relativity - are described in the spotlight topic Defining "now". With all these preparations, physicists can, in principle, assign a time coordinate value ("a time") to any possible events, and describes how fast or how slow processes happen, compared to that time coordinate.

space

In a strict sense: Space as we know it from everyday life: the totality of all locations in which objects can sit, with three dimensions. In a more general sense used by mathematicians, all kinds of sets of points are spaces - a line for instance, which has but a single dimension, or a two-dimensional surface, but also higher-dimensional spaces. Also, in such more general spaces, geometry can be different from the standard Euclidean geometry taught in high schools - such spaces can be curved.

singularity

Irregular boundary of spacetime in general relativity - region where spacetime simply comes to an end. Often, such boundaries are associated with spacetime curvature growing beyond all bounds and becoming infinitely large - so-called curvature singularities (notably Ricci singularities or Weyl singularities - but there are exceptions (for instance a conic singularities). According to general relativity, a singularity exists inside every black hole, and the starting point of any universe described by a big bang model is a singularity as well. The occurrence of singularities is a failure of general relativity - and a strong indication that the theory is incomplete. Instead, one could describe the earliest universe and the interior of black holes using a theory of quantum gravity. More information about singularities can be found in the spotlight texts Spacetime singularities and Of singularities and breadmaking.

quantum theory

The framework for formulating the physical laws that govern the world at microscopic length-scales - the physics of the micro-world, for instance of atoms, atomic nuclei or elementary particles, but also the physics of ultra-precise measurements such as those made by gravitational wave detectors.

The laws of quantum theory are fundamentally different from our everyday experience and from those of classical physics.

The first unusual feature is that, in many cases, quantum theory merely allows statements about probabilities. For instance, in classical physics, one can assign to every particle, at every point in time, a location and a velocity. Whosoever can measure those quantities precisely can, in principle, predict where the particle in question can be found at every point in the future. In quantum theory, all one can assign to a system of particles is an abstract quantum state from which can be derived no precise predictions, but merely the probabilities for detecting a specific particle at a given time in a given place. Whether or not one will really find the particle at that location is governed by chance.

The second unusual feature is a fundamental restriction placed on the exactness of certain measurements (Heisenberg uncertainty relation). For instance, the more precise one measures a particle's location, the less definite any statements one can make about its velocity.

The third feature is how quantum theory came by its name: A number of physical quantities in nature come in little packets, in quanta. For instance, according to quantum theory, electromagnetic radiation is made of tiny quanta of energy called photons.

Examples for quantum theories are quantum mechanics and relativistic quantum field theories such as Quantum electrodynamics or other parts of the standard model of particle physics.

quantum gravity

Theory based both on the effects, concepts and laws of quantum theory and on those of general relativity. To date, no complete such theory exists; the best-known candidate theories are string theory and loop quantum gravity. Some information on the question of quantum gravity can be found in the chapter Relativity and the quantum of Elementary Einstein, starting with the page Border regions of gravity. Selected aspects of quantum gravity are described in the category Relativity and the quantum of our Spotlights on relativity.

point

Elementary "building block" of geometrical entities such as surfaces or more general spaces. For instance, a surface is the set of all its points, of all possible locations on the surface, and all geometrical objects in that surface are defined by the points that belong to them - for instance, a line on the surface is the set of (infinitely many) points.

momentum

Physical quantity that is equal to a body's mass times its velocity (in special relativity: its relativistic mass times its velocity). What makes momentum a useful quantity is that it is conserved - if several bodies interact, the sum of their momenta before and after the interaction is the same. Momentum is neither created nor destroyed, merely passed on from one body to another. In general relativity, momentum is one of a number of quantities (like mass and energy) that acts as a source of gravity.

loop quantum gravity

Candidate for a theory of quantum gravity. Loop quantum gravity is an attempt to apply the concepts and laws of quantum theory directly to the geometry that is at the heart of general relativity. A brief description can be found on the page Loop quantum gravity in the chapter Relativity and the quantum of Elementary Einstein.

lead

Chemical element with the symbol Pb; each lead nucleus contains 82 protons. Lead nuclei, stripped of their electrons, are among the types of heavy ions which are brought into collision in particle accelerators such as the Relativistic Heavy Ion Collider in order to recreate the state of matter in the early universe shortly after the big bang.

inflation

Hypothetical phase in the earliest universe during which the cosmos underwent exponentially growing expansion.

gravity

See gravitation

gravity (gravitation)

In classical physics: An action-at-a-distance force by which all bodies that possess mass attract each other (see Newtonian theory of gravity), synonym: gravitational force. In Einstein's general theory of relativity: The fact that matter that possesses mass, energy, pressure or similar properties distorts spacetime, and that this distortion in turn influences whatever matter might be present. An introduction to the basic ideas of general relativity is provided by the section General relativity of Elementary Einstein. More information about the nature of gravity in general relativity can be found in the spotlight text Gravity: From weightlessness to curvature.

general relativity (general theory of relativity)

Albert Einstein's theory of gravity; a generalization of his special theory of relativity. For information about the concepts and applications of this theory, we recommend the chapter general relativity of our introductory section Elementary Einstein. Further information about many different aspects of general relativity and its applications can be found in our section Spotlights on relativity.

focus

In optics: A focus, also referred to as an image point, is the point where incoming, parallel light rays meet after traveling through a lens. In geometry: For an ellipse all points on the curve are located around two focal points, such that the sum of the distances to each focal point is equal for all points.

cosmology

That branch of physics and astronomy dealing with the structure and development of the universe as a whole. At the core of modern cosmology are the big bang models based on Einstein's general theory of relativity. Their basic features are reviewed in the chapter Cosmology of Elementary Einstein. In order to describe the very early universe, it will be necessary to take the effects of quantum gravity into account - this gives rise to models of quantum cosmology.

big bang

The big bang models are the foundation of modern cosmology. Firmly grounded in Einstein's theory of general relativity, they describe a universe that began in a very hot initial state and has expanded (and cooled down) ever since. They make precise predictions about nucleosynthesis in the early universe, the existence and properties of the cosmic background radiation, and the distribution of distant galaxies in the cosmos, which have been confirmed by astronomical observation. The word "big bang" has two different meanings. In a strict sense, the big bang is a spacetime singularity, a state of infinite density - the initial state the big bang models predict for our universe. In a more general sense, the term is applied to the earliest cosmic eras, in which the universe was exceedingly hot and dense. Further information about these two meanings and why it is important to distinguish between them can be found in the spotlight text A tale of two big bangs. The basic features of the big bang models are reviewed in the chapter Cosmology of Elementary Einstein. Selected aspects of cosmology are described in the category Cosmology of our Spotlights on relativity.