Die problematischen Zwillinge

Warum das so genannte Zwillingsparadoxon nur scheinbar paradox ist

Ein Artikel von Markus Pössel

In Einsteins Spezieller Relativitätstheorie ist es nicht sinnvoll, von „der Zeit“ im Singular zu reden. Wie Zeit vergeht, hängt von der Bewegung ab, und das Paradebeispiel dafür sind die oft genannten hypothetischen Zwillinge.

Zwilling auf Reisen

Einer davon bleibt auf der Erde, während sich der andere auf eine Rundreise mit fast lichtschneller Rakete begibt:

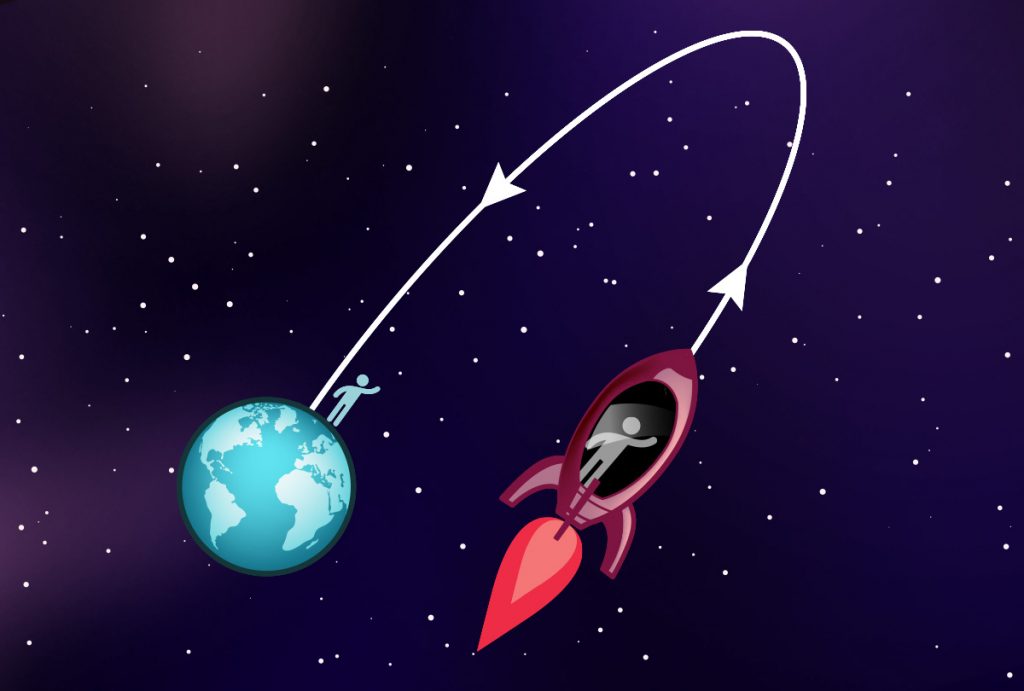
Am Ende der Reise, wenn sich die beiden Zwillinge wieder Aug‘ in Aug‘ gegenüberstehen, ist der daheimgebliebene Zwilling deutlich älter als der Raketenreisende. Es kann zum Beispiel sein, dass auf den Borduhren der Rakete nur zwei Jahre vergangen sind, der gereiste Zwilling auch subjektiv nur zwei Jahre Reisezeit erlebt hat und um eben diese Zeit gealtert ist, während zuhause auf der Erde zwischen Start und Rückkehr ganze 30 Jahre vergangen sind. Treffen die Zwillinge am Ende wieder zusammen, kann man ihnen diesen Altersunterschied deutlich ansehen.

Soweit, so ungewohnt, aber unbestreitbar Realität: Nicht mit Raketen, aber mit Elementarteilchen in Teilchenbeschleunigern kann man solch ein Rundreiseexperiment tatsächlich durchführen und dabei feststellen: die „innere Uhr“ eines Elementarteilchens im Kreisbeschleuniger geht deutlich langsamer als die eines Teilchens derselben Sorte, das neben dem Beschleuniger ruht (vergleiche die Seite Die Relativität von Raum und Zeit im Kapitel Spezielle Relativitätstheorie von Einstein für Einsteiger).

Eine Frage der Gleichberechtigung

Zum Zwillingsproblem und sogar zum scheinbaren Zwillingsparadoxon wird das Szenario, wenn man sich bemüht, das Phänomen mit der sogenannten Zeitdilatation zu erklären, einem grundlegenden und ebenfalls sehr ungewohnten Effekt der Speziellen Relativitätstheorie. Dieser Effekt betrifft einen Beobachter (genauer: Inertialbeobachter), etwa auf einer im Weltraum frei schwebenden Raumstation. Für solch einen Beobachter folgt aus der Speziellen Relativitätstheorie ganz allgemein: Für relativ zu ihm bewegte Uhren, seien es die Uhren einer zweiten, vorbeifliegenden Raumstation, sei es die Uhr einer wild umherkurvenden Rakete, stellt dieser Beobachter im Vergleich fest, dass sie langsamer gehen als seine eigenen. Wenn er die Zeitanzeigen vergleicht, kommt er zu dem Ergebnis: Während jeder Sekunde, die auf seiner eigenen Uhr vergeht, vergeht auf den bewegten Uhren jeweils weniger als eine Sekunde. Die Verlangsamung gilt nicht nur für Uhren, sondern alle Vorgänge auf der bewegten Raumstation oder in der Rakete sind aus Sicht unseres Beobachters in genau demselben Maße verlangsamt. Ein Fünf-Minuten-Ei, gekocht in der vorbeifliegenden Raumstation, benötigt im Vergleich mit der neben dem Kochtopf stehenden Eieruhr weiterhin nur fünf Minuten. Aber gemessen auf der Uhr unseres Beobachters, der Ei und Eieruhr vorbeifliegen sieht, dauern Kochvorgang und das Vorrücken des Eieruhr-Zeigers um fünf Minuten beide deutlich länger als fünf Minuten.

Entscheidende Eigenschaft der Zeitdilatation ist, dass sie in bestimmten Situationen auf Gegenseitigkeit beruht. Bei zwei Beobachtern, jeder in seiner frei treibenden Raumstation, die mit konstanter Geschwindigkeit aneinander vorbeifliegen, geht für jeden der beiden die Zeit in der jeweils anderen Raumstation langsamer. (Wer das bereits für einen Widerspruch hält, dem sei das Vertiefungsthema Die Dialektik der Relativität empfohlen.)

Mit Hilfe der Zeitdilatation, die oft verkürzt zu „Bewegte Uhren gehen langsamer“ zusammengefasst wird, kann man versuchen, den Zwillingseffekt zu erklären. Kein Wunder, dass der reisende Zwilling langsamer altert – der Daheimgebliebene kann schließlich mit der Zeitdilatation argumentieren: Bewegte Uhren gehen langsamer, und so ist auch auf der Uhr des bewegten Zwillings weniger Zeit vergangen als auf der des daheimgebliebenen, wenn die beiden sich bei der Rückkehr wiedertreffen.

Schön und gut – aber warum kann man die Argumentation nicht umkehren? Bewegung ist doch relativ, so könnte man argumentieren. Was hält den Zwilling in der Rakete davon ab, sich als ruhend zu betrachten? Aus dieser Sicht wäre es der Zwilling auf der Erde, der sich bewegen, sich erst entfernen und dann wieder annähern würde, und gemäß „bewegte Uhren gehen langsamer“ könnte der Raketen-Zwilling ableiten, dass auf der Uhr des Erd-Zwillings bis zum letztendlichen Zusammentreffen weniger Zeit vergehen müsste als auf seiner eigenen. Jeder der Zwillinge, so könnte man meinen, hat dasselbe Recht zu argumentieren, der jeweils andere müsse langsamer altern als er selbst. Und doch kann nach Rückkehr der Rakete, wenn die Zwillinge ihre Uhren direkt vergleichen können, nur einer Recht haben. Ein Widerspruch – ein Zwillings-Paradoxon?

Die Sonderrolle der Inertialsysteme

Zur Auflösung des scheinbaren Widerspruches muss man etwas genauer betrachten, für welche Beobachter die Zeitdilatation gilt und für welche nicht. In der obigen Beschreibung ist es nur in Klammern erwähnt worden: Dass bewegte Uhren langsamer gehen gilt genau aus Sicht von Inertialbeobachtern, von Beobachtern, deren Raumstationen Inertialsysteme sind. Was das heißt, deuten die oben gewählten Beispiele der frei im Weltall treibenden Raumstationen an: In einem Inertialsystem herrscht perfekte Schwerelosigkeit. Ein Objekt, auf das keine äußeren Kräfte wirken, bleibt im Inneren einer solchen Raumstation unbewegt schweben oder bewegt sich mit konstanter Geschwindigkeit auf gerader Bahn.

Es gilt also für jeden der Zwillinge zu prüfen: Ist er ein Inertialbeobachter – und beobachtet daher an allen relativ zu ihm bewegten Objekten die Zeitdilatation der Speziellen Relativitätstheorie?

Eine leidige Komplikation: Der Zwilling auf der Erde ist kein Inertialbeobachter, denn er befindet sich in einem Schwerefeld: Objekte, die er loslässt, fallen beschleunigt zu Boden. Dem lässt sich auf zweierlei Weise Rechnung tragen: Zum einen kann man sich daranmachen, im Rahmen von Einsteins Gravitationstheorie, der Allgemeinen Relativitätstheorie, auszurechnen, wie das Schwerefeld den Lauf der Uhren des daheimgebliebenen Zwillings beeinflusst. Das Ergebnis: Im Vergleich mit den Altersdifferenzen zum fast lichtschnellen Zwilling ist der Einfluss vernachlässigbar klein, und der daheimgebliebene Zwilling darf sich zumindest näherungsweise auf die Zeitdilatation berufen um das Jüngerbleiben des anderen Zwillings zu erklären. Wem das zu wenig ist, der kann die Situation leicht abändern und den daheimgebliebenen Zwilling fernab im All in einer frei treibenden Raumstation auf die Rückkehr des anderen Zwillings warten lassen, so dass er sich ganz gewiss in einem Inertialsystem befindet. Ebenso gewiss ist dieser Zwilling daher berechtigt, die Zeitdilatationsformel anzuwenden: Von seinem Bezugssystem aus beurteilt gehen bewegte Uhren langsamer.

Was ist mit dem raketenreisenden Zwilling? Er befindet sich ebenfalls nicht in einem Inertialsystem. Würde er einfach frei, geradlinig und mit konstanter Geschwindigkeit von der Erde (oder der Raumstation) wegfliegen, würde er schließlich immer weiterfliegen und niemals zurückkehren. Um zurückzukommen, ist zwangsläufig eine Beschleunigungsphase nötig, sei es ein Abbremsen und anschließendes Beschleunigen in Richtung Erde, sei es das Fliegen einer Kehrtwende. In beiden Fällen spürt der Raketeninsasse die Beschleunigung, genau so, wie die meisten Leser es aus dem Alltag vom Autofahren her kennen dürften: Beim Abbremsen zieht ihn eine Kraft aus dem Sitz nach vorne, beim Wieder-Beschleunigen drückt sie ihn in seinen Sitz, und beim Kurvenfliegen fühlt er sich seitwärts gezogen. Die Beschleunigungen spürt auch jedes Objekt, das der Raketeninsasse in seiner Kabine loslässt, und das zeigt: Aufgrund der unausweichlichen Beschleunigungsphase befindet sich der Zwilling in der Rakete nicht durchgehend in einem Inertialsystem. Er darf daher die Formel für die einfache Zeitdilatation gar nicht anwenden.

Bei genauem Hinsehen sind die beiden Zwillinge also nicht gleichberechtigt – derjenige in der Rakete muss sich zwangsläufig Beschleunigungen aussetzen, will er zum anderen Zwilling zurückkehren. Damit löst sich auch das scheinbare Paradoxon auf: Nur die Folgerung des daheimgebliebenen Zwillings, die bewegte Uhr des Raketenzwillings gehe langsamer und daher sei dieser Zwilling beim Zusammentreffen jünger, ist berechtigt. (Der Frage, wie man sich die Auswirkung der Beschleunigung vorstellen sollte – beeinflusst sie direkt den Gang der Uhren in der Rakete? – ist das Vertiefungsthema Zwillinge und Wanderer gewidmet.)

Weitere Informationen