The case of the travelling twins
Why the so-called “twin paradox” isn’t really a paradox
An article by Markus Pössel
In Einstein’s special theory of relativity, there is no such thing as “time” in the singular. Time passes differently for different observers, depending on the observers’ motion. The prime example is that of the two hypothetical twins: One of them stays at home, on Earth. The other journeys into space in an ultra-fast rocket, nearly as fast as the speed of light, before returning home:
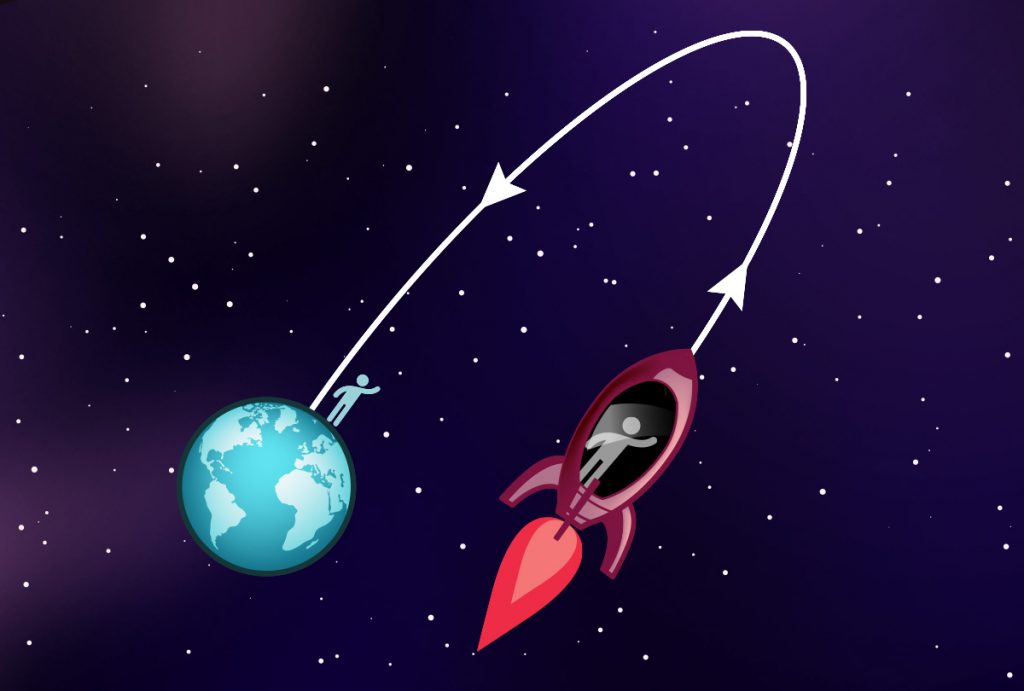
Afterwards, when the twins are reunited on Earth, the travelling twin is markedly younger, compared to her stay-at-home sibling. The exact age difference depends on the details of the journey. For example, it could be that, aboard the space-ship, two years of flight-time have passed – on-board clocks and calendars show that two years have elapsed, and both spaceship and travelling twin have aged by exactly that amount of time. On Earth, however, a whopping 30 years have passed between the spaceship’s departure and its return. Just like all other humans on the planet, the twin on Earth has aged by 30 years during that time. Seeing the two (ex?) twins side by side, the difference is striking.
So far, so strange, but undoubtedly real. Space-travel with speeds close to that of light may be unfathomably far beyond the reach of current technology. But sending elementary particles on round trips in a particle accelerator at 99.99999 percent of light speed is routine. The result is in precise agreement with the predictions of special relativity – the “inner clock” of such a travelling particle runs much slower than that of a particle of the same species that remains at rest (cf. the page The relativity of space and time in the section Special Relativity of Elementary Einstein).
Turning the tables?
The reason the case of the travelling twins is also known as the “twin problem” or even the “twin paradox” is the following. From the point of view of the twin on Earth, one can explain the age difference by appealing to time dilation, a basic concept of special relativity. It involves an observer (more precisely: an inertial observer), for instance an observer that lives on a space station floating through empty space. For such an observer, special relativity predicts the following: For any moving clock, that observer will come to the conclusion that it is running slower than his own. Whether it is a clock on another space station floating past or a clock on an engine-driven rocket, in the time it takes for a second to elapse on the observer’s own clocks, less than a second will have elapsed on the moving clock. This slowdown is true not only for clocks, but for everything that happens on the moving space station or in the flying rocket. All processes taking place on these moving objects will appear slowed down for our observer.
Characteristically, there are situations where time dilation is mutual. For instance, if there are two observers drifting through space, each on his or her own space station, and if those two space stations are in relative motion, then for each observer, the time in the other space station appears to run slower than for himself. (If that already sounds like a paradox to you, you might want to read the spotlight topic The dialectic of relativity.)
With the help of time dilation – often abbreviated to “moving clocks go slower” – one can try to explain what happens to the twins. No wonder the travelling twin ages less! After all, the twin on Earth can invoke time dilation: Moving clocks go slower, and so do the clocks of the moving twin. On these slower-moving clocks – and, by extension, in the whole spaceship – less time passes than on Earth, in other words: when the travelling twin returns, he is younger.
No paradox so far. But why can’t the travelling twin turn the tables on her sibling? After all, motion is relative. Why can’t the twin in the spaceship define herself as being at rest? From that point of view, it would be Earth that moves away before returning to the spaceship. And if that is so, couldn’t the travelling twin apply time dilation (“moving clocks are slower”) to everyone who remained on Earth? By that argument, shouldn’t it be the humans on Earth that are younger than expected once the twins are reunited? If both twins are on an equal footing, then each one should be allowed to onsider herself at rest and invoke time dilation. But in the end, when the twins meet again, only one of them can be right – then, there cannot be any ambiguity: either the one twin is younger, or the other (or, of course, both twins’ arguments are wrong, and they have aged exactly the same). A contradiction – a twin paradox?
The importance of inertial observers
To resolve the contradiction, a closer look at time dilation is needed – in which situations do moving clocks indeed go slower? In the above text, the key criterion was hidden in parentheses: For the dictum “Moving clocks go slower” to hold, you must be an inertial observer. The example of freely floating space stations above gives a flavour of what this qualification means: In an inertial reference frame, all objects are perfectly weightless. For such observers, an object upon which no external forces act (for instance, that is neither pushed nor pulled) either remains at rest or moves with a constant speed along a straight line.
There’s the litmus test for each twin: Is she an inertial observer, and thus entitled to apply the time dilation formula, concluding that moving clocks go slower?
An unfortunate complication: The twin that remains on Earth is no inertial observer. She’s in a gravitational field in which objects fall down instead of remaining at rest. There are two possible ways to proceed. Either one can use Einstein’s theory of gravity, general relativity, and calculate how the gravitational field influences the twin on Earth. The result is that, in the given situation, Earth’s gravity does not make an appreciable difference. If we ignore Earth’s gravity and treat the twin on Earth as an inertial observer, our results regarding the relative aging of the two twins will be correct, give or take a few fractions of a second. If we choose situations in which the twins’ eventual age difference is counted in years, gravity will not matter.
Alternatively, one could re-define the situation by having the non-travelling twin wait not on Earth, but in a freely floating space station in deep space, far away from any massive objects. That would definitely make her an inertial observer.
In both cases, the result is that the non-travelling twin has the right to apply the simple time dilation formula, and to conclude that her travelling sibling will be younger when they meet again.
What about the travelling twin? She’s not an inertial observer, either, at least not the whole time. If she simply coasted along with constant speed along a straight line, she could never return to Earth (or, in the alternative version, to the other twin’s space-station). In order to return, it is crucial that the travelling twin either come to a stop and accelerate towards Earth or, alternatively, fire her engine to force her spaceship onto a tight curve to point it back towards Earth. In both cases, the travelling twin feels the acceleration – decelerating, her body feels a pull in the direction of flight, re-accelerating, she is pressed into her seat, in flying a turn, she is pulled sideways. Acceleration is inevitable – and while she is accelerating, the travelling twin definitely isn’t an inertial observer. For instance, during a braking phase, objects afloat inside the spaceship’s cabin will not just float or move with constant speed – they will be accelerated toward the front of the spaceship. And in contrast with the twin on Earth, there is no slight redefinition that will do away with these acceleration phases. There’s no way around it: At least for some of the time, the travelling twin isn’t an inertial observer.
Thus the apparent paradox is resolved. The twins are not on an equal footing. The accelerated twin cannot just apply the simple time dilation formula, while her sibling on Earth can. The latter twin’s conclusion that the clocks of the travelling twin run slower, and that the travelling twin is thus younger when they meet again, is valid. (So what role does the acceleration play in this? Find out more in the spotlight topic Twins on the road.)
Further Information
The basics of special relativity – the proper theory to answer all questions about these twins – can be found in Elementary Einstein in the section Special Relativity.
Related Spotlight topics on Einstein-Online can be found in the section Special Relativity.
Colophon
is the managing scientist at Haus der Astronomie, the Center for Astronomy Education and Outreach in Heidelberg, and senior outreach scientist at the Max Planck Institute for Astronomy. He initiated Einstein Online.
Citation
Cite this article as:
Markus Pössel, “The case of the travelling twins” in: Einstein Online Band 04 (2010), 01-1007