Das Ende der Privilegien

Inwiefern in der Allgemeinen Relativitätstheorie alle Beobachter gleichberechtigt sind – und warum man trotzdem sagen kann, die Erde laufe um die Sonne und nicht umgekehrt

Ein Artikel von Markus Pössel

Läuft die Erde um die Sonne – oder die Sonne um die Erde? Oder sind etwa beide Ansichtsweisen gleichberechtigt? Allgemeiner gefragt: Sind alle Beobachter gleichberechtigt, oder gibt es privilegierte Beobachter? Andererseits: Was soll es überhaupt heißen, ein Beobachter sei vor anderen privilegiert?

Auch auf die Gefahr hin, dass der Leser den Eindruck bekommt, wir würden mit den Fragen vom Hundertsten ins Tausendste kommen: Es lohnt sich, sogar noch einen Schritt zurückzutreten und mit der Frage zu beginnen, was denn eigentlich im Hinblick auf solche Fragen mit dem Begriff „Beobachter“ gemeint ist.

Beobachter

Die Antwort: Ein Beobachter ist jeder, der es unternimmt, Raum und Zeit um sich herum und alles, was darin passiert, zu vermessen. Die folgende Abbildung steht für ein einfaches Beispiel – einen Beobachter in einer frei treibenden Raumstation:

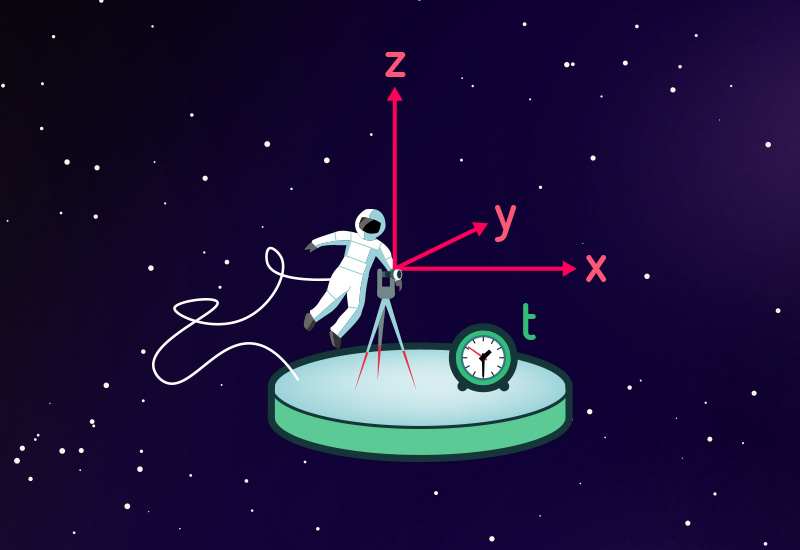
Als natürlichen Bezugspunkt verwendet jeder Beobachter seinen eigenen Ort; relativ zu sich selbst ordnet er allen anderen Orten Raumkoordinaten zu, jedem Ort drei Zahlen, anhand derer sich der Ort eindeutig identifizieren lässt. Dazu kann er beispielsweise ein kartesisches Koordinatensystem mit den Achsen x,y,z verwenden, aber beispielsweise auch ein geografisches Koordinatensystem aus geografischer Länge, Breite und der Höhe über dem Meeresspiegel, oder eine Vielzahl anderer möglicher Raumkoordinaten. Außerdem definiert solch ein Beobachter eine Zeitkoordinate – eine Vorschrift, nach der sich jedem Ereignis eine Zahl zuordnen lässt. Diese Zahl gibt den Zeitpunkt an, zu dem das Ereignis stattfindet.

Denkbar sind unendlich viele verschiedene Beobachter. Sie unterscheiden sich nicht nur durch ihren Standort und ihre Bewegung, sondern es sind zudem unendlich viele Variationen der Vorschriften möglich, nach denen ein Beobachter die Welt mit Raum- und Zeitkoordinaten überzieht. Nach unserer möglichst umfassend gewählten Definition ist der Begriff „Beobachter“ äquivalent zu „Raum-Zeit-Koordinatensystem“ oder kurz „Koordinatensystem“.

Zur Gleichberechtigung der Beobachter

Damit zurück zur Frage der Gleichberechtigung. Gibt es Beobachter, die vor anderen Beobachtern ausgezeichnet sind, oder sind alle Beobachter gleichberechtigt? Oder auch: Gibt es bevorzugte Koordinatensysteme?

In der klassischen Mechanik, wie sie lange vor Einstein formuliert wurde, ist die Antwort: Ja, es gibt privilegierte Beobachter. Der Hintergrund ist der folgende: Jeder Beobachter kann festhalten, wo sich Objekte befinden. Um die Position eines Objektes zu bestimmen, verwendet er seine Ortskoordinaten. Er kann außerdem die Geschwindigkeit von Objekten bestimmen, sprich, wie sich ihre Position mit der Zeit verändert. Auch ihre Beschleunigung kann der Beobachter bestimmen, nämlich wie sich die Geschwindigkeit eines Objekts mit der Zeit ändert. Entscheidend ist, dass es zwei Klassen von Beobachtern gibt.

Für Beobachter der ersten Klasse gilt: Wenn sie alle Kräfte, die Objekte aufeinander ausüben – elektrische oder magnetische Kraft, Schwerkraft sowie direkte Druck- und Zugkräfte – berücksichtigen, dann gilt: Für jedes Objekt ist die Summe der darauf wirkenden Kräfte gleich der Masse mal der Beschleunigung des betreffenden Objekts.

Anders für Beobachter der zweiten Klasse. Für sie geht die Gleichung „Kraft gleich Masse mal Beschleunigung“ nur auf, wenn sie außer denjenigen Kräften, die Objekte aufeinander ausüben, noch weitere Kräfte berücksichtigen, die gewissermaßen von außen auf alle Körper wirken und in der Physik Scheinkräfte oder Trägheitskräfte genannt werden. Zwei Beispiele: Zum ersten ein Beobachter, der Karussell fährt und in dessen Koordinatensystem die Welt dementsprechend in ständiger Drehung begriffen ist. Er muss in seinen Gleichungen jeweils eine Zentrifugalkraft berücksichtigen, die alle Objekte von der Drehachse weg nach außen zieht – anders kann er die Bewegungen der Objekte nicht erklären. Zum zweiten ein Beobachter in einer beschleunigten Rakete. Er muss eine Scheinkraft einführen, um zu erklären, warum beispielsweise ein Objekt, das er loslässt, aus seiner Sicht beschleunigt in Richtung Raketenboden gezogen wird.

Allein aufgrund der physikalischen Gesetze – der Gesetze der Mechanik – sind demnach in der klassischen Physik Beobachter der ersten Klasse ausgezeichnet. Für sie ist die Mechanik deutlich einfacher als für die Beobachter der zweiten Klasse, da sie die Bewegung der diversen Objekte beschreiben können, ohne dass in ihren Gleichungen zusätzlich zu den herkömmlichen Kräften noch Scheinkräfte auftauchen. In genau dieser Weise sind auch Beobachter, die frei im Weltraum schweben, relativ zur Sonne ruhen (und relativ zum fernen Fixsternhimmel nicht rotieren) vor Beobachtern auf der Erde ausgezeichnet. Für Erstere sind die Gesetze der Mechanik einfach; Letztere müssen Scheinkräfte wie Zentrifugalkraft und Corioliskraft berücksichtigen, um die Bewegung etwa der Planeten oder fallender Körper zu erklären. In diesem Sinne legen die Gesetze der Physik tatsächlich nahe: Die Erde läuft um die Sonne, und nicht umgekehrt.

Freilich ist die klassische Mechanik nicht der Physik letzter Schluss. Seit Einsteins Arbeiten von 1905 wissen wir, dass ihre Gesetze nur näherungsweise gelten – einfach gesagt immer dann, wenn die Geschwindigkeiten der betrachteten Körper klein sind im Vergleich zur Lichtgeschwindigkeit . Kommen Geschwindigkeiten nahe der Lichtgeschwindigkeit ins Spiel, müssen wir eine genauere Theorie von Raum und Zeit verwenden, die Spezielle Relativitätstheorie. Dort gelten etwas andere Gesetze der Mechanik. Im Hinblick auf unsere Frage nach der Gleichberechtigung der Beobachter kommt man freilich zu ganz ähnlichen Ergebnissen wie in der klassischen Mechanik: Auch in der Speziellen Relativitätstheorie gibt es Beobachter, für die die Gesetze der Physik besonders einfach sind und die keinerlei Scheinkräfte bemühen müssen, um die Bewegung der Objekte um sie herum zu erklären. Das sind die Inertialbeobachter, die üblicherweise gemeint sind, wenn im Rahmen der Speziellen Relativitätstheorie von Beobachtern die Rede ist.

Allgemeine Relativitätstheorie

Nun hat allerdings auch die Spezielle Relativitätstheorie nur einen eingeschränkten Geltungsbereich. Sobald die Gravitation eine Rolle spielt – und das ist in unserem Beispiel von Sonne und Erde manifest der Fall – kann die Theorie uns nicht weiterhelfen. Dann müssen wir die Allgemeine Relativitätstheorie bemühen, und im Rahmen dieser Theorie erhält man auf unsere Frage nach der Gleichberechtigung eine ganz andere Antwort. Dort gibt es keinen prinzipiellen Unterschied zwischen der Gravitation und den Scheinkräften, wie sie beispielsweise ein Beobachter in einer beschleunigten Raketenkabine spürt. Diese Nicht-Unterscheidbarkeit ist sogar eines der Prinzipien, aus denen heraus Einstein seine Theorie entwickelt hat, das so genannte Äquivalenzprinzip. Damit entfällt das Unterscheidungskriterium, das in der klassischen Mechanik und der Speziellen Relativitätstheorie so gute Dienste geleistet hat um Beobachter erster und zweiter Klasse auseinanderzuhalten. Wie sich herausstellt, gibt es auch über dieses Kriterium hinaus keine Eigenschaft der physikalischen Gesetze, die es ermöglichen würde, einige Beobachter gegenüber anderen Beobachtern auszuzeichnen, keine absoluten Strukturen, an denen sich ein Unterschied festmachen ließe. In diesem Sinne sind in der Allgemeinen Relativitätstheorie tatsächlich alle Beobachter gleichberechtigt. (Eine Anmerkungen dazu, wieweit diese Aussage reicht, bietet die Fußnote.)

Heißt das, dass im Rahmen der Allgemeinen Relativitätstheorie der Beobachter auf der Erde mit gleichem Recht erklären kann, die Sonne drehe sich um die Erde, wie der Beobachter neben der Sonne behaupten kann, die Erde drehe sich um die Sonne? Ja und nein. Was die grundlegenden Naturgesetze angeht, lässt sich tatsächlich keiner der beiden Beobachter vor dem anderen auszeichnen. Aber es gibt eine andere, weniger grundlegende Möglichkeit der Unterscheidung: In einer konkreten Situation, und nur auf diese Situation bezogen, kann nach wie vor ein Koordinatensystem einfacher und natürlicher sein als ein anderes. Eine solche Entscheidung lässt sich zwar nicht für jede Situation treffen, aber im Falle von Erde und Sonne fällt sie vergleichsweise eindeutig aus: Auch im Rahmen der Allgemeinen Relativitätstheorie ist es einfacher, die Bewegung von Erde und Sonne aus Sicht eines Beobachters zu beschreiben, der relativ zur Sonne (und zum fernen Fixsternhimmel) ruht. In diesem – freilich gegenüber der klassischen Mechanik abgeschwächten – Sinne ist es weiterhin legitim zu sagen, die Erde drehe sich um die Sonne und nicht umgekehrt.

Eigentlich ist unsere Reise durch die verschiedenen Theorien an dieser Stelle noch nicht zuende. Denn auch die Allgemeine Relativitätstheorie hat ihre Grenzen. Sie vernachlässigt die Effekte der Quantenphysik, die vor allem in der Mikrowelt eine wichtige Rolle spielen. Allerdings kann zur Zeit noch niemand sagen, wie eine Theorie der Quantengravitation im Einzelnen aussehen wird. Viele Forscher sind der Meinung, dass auch solch eine Theorie die Beobachtergleichberechtigung der Allgemeinen Relativitätstheorie respektieren wird, aber eine endgültige Antwort auf die Frage der Gleichberechtigung in der Quantengravitation kann heute noch niemand geben. Wir müssen uns mit den Antworten bescheiden, die die heute bekannten physikalischen Theorien – klassische Mechanik, Spezielle Relativitätstheorie, Allgemeine Relativitätstheorie – liefern, jede für ihren Geltungsbereich.

Weitere Informationen