…that all coordinate systems are created equal

Why, in general relativity, all observers are on an equal footing – and why, nevertheless, you can say that the earth orbits the sun, but not the other way around

An article by Markus Pössel

Does the Earth orbit around the sun – or is it the other way around? Or are both points of view equally valid? More generally: Are all observers on an equal footing, or are some observers privileged? And what does “privileged” mean, anyway?

In order to answer these questions, it proves helpful to go back by one further step: What, when we get down to it, is an “observer”?

Observers and coordinate systems

The answer, at least in this particular context, is the following: An observer is anyone who casts a mathematical net over time and space, establishing conventions to describe locations in space and points in time. The following illustration represents a simple example: an observer aboard a space-station, floating freely through deep space:

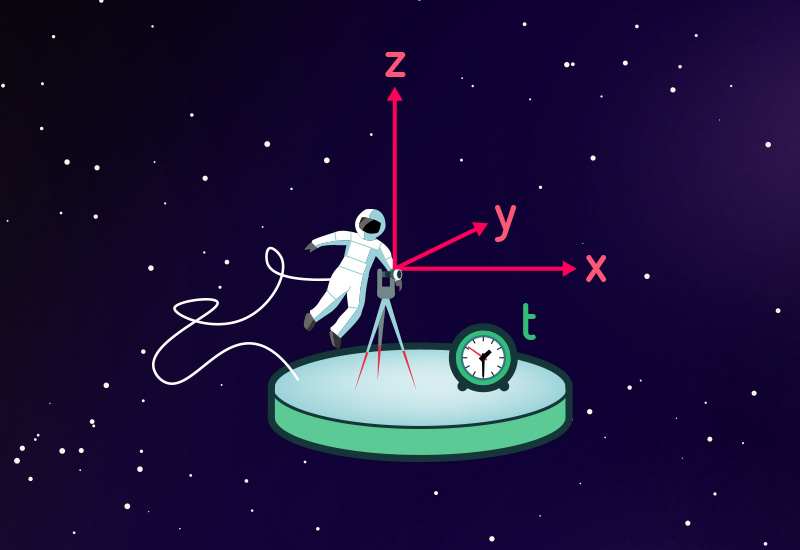
The natural reference point for such an observer is his own location in space; relative to that location, he or she assigns space coordinates, three numbers per point, that serve as unique identifiers for each location. One way to do that is the Cartesian coordinate system familiar from school, with its axes x, y and z hinted at in the illustration. Another would be the geographical coordinate system of latitude and longitude, plus height above sea level. Countless further possibilities exist. In addition to surveying space, the observer defines a time coordinate – a way to ascribe to every event one number which labels the point in time when that event happens.

All in all, there is a plethora of different possible observers – each with a specific way of imposing mathematical order onto the world. The differences lie not only in the different location of the observers, or their different motions, but in the infinity of variations that is possible for conventions of how to choose space and time coordinates. In fact, in our definition, the term “observer” is equivalent to that of “space-time-coordinate system”, or just “coordinate system”.

After this excursion, back to our original question: Are there observers that are somehow special, that are privileged? Or are all observers on an even footing? To use a more whimsical formulation: Are all coordinate systems created equal?

Observers in classical mechanics

In classical mechanics, formulated long before Einstein’s time, the answer is that there are indeed privileged observers. Their privileged status comes about in the following way: Every observer can chart where objects are, using his particular brand of space coordinates. Every observer can also determine an object’s velocity – a measure of how it changes its position over time, and also the way that the object’s velocity changes over time, namely its acceleration. Once all this is done, it turns out that there are two classes of observers.

For observers belonging to the first class, the following holds true: If all forces with which objects can act on each other – the electric force, the magnetic or the gravitational force, as well as all forces with which solid objects can pull at or push each other directly – are taken into account then, for every object, the sum of the forces acting upon it is equal to its mass times its acceleration.

The situation is different for observers belonging to the second class. For them, the equation “Force equals mass times acceleration” only works if, in addition to the forces with which objects act on each other, they postulate the existence additional forces that are somehow “external”. These latter forces are called inertial forces.

Two examples: In the first example, the observer rides a merry-go-round. From an outside point of view, his coordinate system is in a state of constant rotation. In his equation, such a rotating observer needs to include a centrifugal force – a force pulling all objects away from the axis of rotation – in order to explain how objects move. As another example, consider an observer aboard a spaceship. While the rocket engines are switched on, that observer has to introduce an inertial force to explain why, from his point of view, all objects appear to have an inborn tendency to fall towards the cabin floor.

Simply considering the laws of physics (more precisely, of mechanics), the observers in the first class are privileged. For them, mechanics is markedly more simple than for observers in the second class. They can describe the motions of bodies without introducing any additional forces – inertial forces – into their equations.

In exactly that way, an observer floating in space, at rest relative to the sun (and not in rotation relative to the distant stars) is privileged, compared to an observer on earth. For the floating observer, the laws of mechanics are simple; the observer on earth must take into account additional, inertial forces such as the centrifugal force or the Coriolis force to explain the motion of the planets or of falling bodies.

Physics is simpler for the floating observer; from that observer’s point of view, the earth orbits the sun. For the observer on earth, for whom the sun orbits his home planet, the laws of physics are more complicated. Judging by simplicity of the laws of physics, the floating observer’s point of view is more natural. In that sense, the laws of physics indeed suggest that the earth orbits the sun, not the other way around.

From classical mechanics to relativity

The situation is very similar in special relativity. In that theory, just as in classical mechanics, some observers are more equal than others. Privileged observers exist, for whom the laws of physics are especially simple. For other observers, physics is more complicated due to the presence of inertial forces. The privileged observers are called inertial observers. When someone refers to an observer in the context of special relativity, chances are that what is meant is an inertial observer.

In general relativity, on the other hand, the situation is markedly different. In that theory, there is no fundamental difference between gravity and inertial forces. Their equivalence, enshrined in what is called the equivalence principle, was a key premise from which Einstein developed his theory in the first place. With this equivalence, there is no strict division between first class or second class observers – in general relativity, the distinction that reigned supreme in both classical mechanics and special relativity is moot.

Furthermore, it turns out that, in general relativity, there is no other way to mark out some observers as special; there are no structures allowing one to identify privileged observers. Instead, all observers, all coordinate systems are created equal, with equal rights before the (physical) laws. There is no class of privileged observers for which the laws of physics are fundamentally more simple than for everyone else. (In this footnote, the scope of that statement is explored a little further.)

Does that mean that, in general relativity, the floating observer declaring the earth to be orbiting the sun, and the observer on earth declaring the sun to orbit to earth, are equally correct? Yes and no.

As far as the laws of physics are concerned, the floating observer is indeed no better than the one on earth. But there is another, less fundamental distinction: In a specific situation, it is possible for some coordinate systems to yield a more simple and thus more natural description of what’s going on than others. The coordinate systems in question are not advantageous for every situation, only for that particular one.

The bad news is that even that very restricted form of privilege exists only in very simple cases – once matters get more complicated, there is no general way to identify coordinate systems favoured by the situation in question. The good news is that the case of a planet like the earth orbiting a significantly more massive sun is simple enough to allow the statement: even within the framework of general relativity, it is simpler to describe the motions of sun and earth from the point of view of an observer that is at rest relative to the sun (and the far-away stars). In that way, even in general relativity, one can make a case for the statement that the earth orbits the sun, instead of the other way around – although that case is much weaker than it was in classical mechanics

Further Information