What figure skaters, orbiting planets and neutron stars have in common

Some information about what is called the conservation of angular momentum, and its consequences for neutron stars, black holes and the matter disks around them

An article by Markus Pössel

Some things, you can depend on – at least in physics. Even for a system as confusing as a cloud of particles in seemingly chaotic motion, there are some physical quantities that remain constant. Physicists call them “conserved quantities”, and the best-known example is energy: Energy may be converted from one form into another – say, from radiation energy to thermal energy. But the sum of all these different types of energy, the total energy, remains constant. Energy can be pumped into a system, or extracted from it. But it can never simply vanish, or be created from nothing.

Energy is not the only physical quantity with this property. Another important example for a conserved quantity is angular momentum. Which brings us to the common physics behind figure-skating, planetary orbits, and the rotation of neutron stars.

Angular momentum defined

For an object orbiting a central point or turning on an axis, angular momentum is the product of the object’s mass times its distance from centre (or axis) times the velocity at which it orbits around the centre.

There are two subtleties in this definition. Strictly speaking, the product doesn’t involve the total velocity, only that part of it which takes the body neither towards nor away from the central point or the axis. However, for circular or near-circular orbits as in the following examples, the difference is negligible – to keep matters simple, I shall talk merely of a body’s “orbital velocity”. Secondly, the point of reference in defining distance and sideways velocity need not be the centre, or a point on the axis. However, in the following examples, this is the most convenient choice and we shall ignore the other possibilities.

Angular momentum is conserved, and that is why figure-skaters can perform dazzlingly fast spins. First, with arms and leg stretched out, the figure-skater’s rotation is slow:

His whole body is turning on a vertical axis. All the different parts of it – except for the tiny portion directly where the axis intersects the body – have non-zero angular momentum. For each portion of the body, this angular momentum is given by the mass times the distance from the central axis times the orbital speed.

If the figure-skater now brings his arms and legs in line with the rest of his body, as in the illustration below, the distance of those body parts to the axis of rotation decreases significantly. Yet the total angular momentum must remain the same (the amount of angular momentum the figure-skater imparts on his surroundings, for instance on the air around him, is negligible). If, in a product of several factors, one factor becomes smaller, yet the product is to remain the same, at least one of the remaining factors must grow larger. For our figure-skater, the compensating factor is the speed of his rotation, which increases markedly. The result is a very fast spin:

Figure-skating is part of many people’s everyday experience (all the more if we include the second-hand experience provided by television). However, as far as angular momentum is concerned, it is rather complicated – to see how much faster the figure-skater should spin, you need to add up all the contributions to angular momentum from the different body parts. Much simpler, but also literally “far out” is the following situation: A planet orbiting the sun.

Planetary orbits

The orbit of a lonely planet around a central body has the shape of an ellipse. Here is a sketch (not to scale):

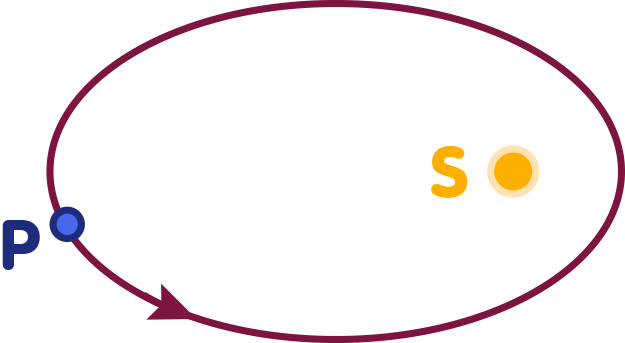
What keeps the planet on its orbit is the sun’s gravitational influence – wherever the planet is in the above figure, the sun always exerts a pull towards its own position, marked in the figure as S. Furthermore, the planet is well isolated from its environment. In this kind of situation, the laws of mechanics tell us, the planet’s angular momentum is conserved. (This is directly connected with one of the subtleties mentioned above – the sun can only pull the planet directly towards itself. This changes only that part of the planet’s velocity directed towards the sun, precisely the component that does not play a role in the definition of angular momentum.)

Using the above definition to calculate the angular momentum with respect to the location of the sun, the product of the planet’s mass, its orbital velocity and its distance from the sun should be constant. But on an orbit like this, sometimes the planet is closer to the sun, and sometimes farther away. In the figure, once the planet has reached the far right of the ellipse, it is closer to the sun than at any other point of its orbit. In order for angular momentum to remain constant, one of the other factors has to increase as the distance decreases. The mass must remain constant, which leaves the planet’s velocity. (For typical orbital velocities, the fact that by this increase of the velocity, the [relativistic] mass increases by a tiny amount as well, is negligible.)

The result is a fundamental law of planetary motion called Kepler’s second law: Whenever its orbit takes a planet closer to the sun, the planet moves faster; whenever it is far away from the sun, slower, and these variations in speed occur in exactly the proper way to ensure the conservation of angular momentum.

Fast-spinning stellar corpses

Among the most impressive applications of the conservation law for angular momentum are collapsing stars – typically stars that have exhausted the fuel necessary for nuclear fusion, leading to a collapse of their core regions. A typical star will rotate at least a little. For instance, our sun takes a month to revolve on its axis (approximately, that is – especially as not all parts of the sun have the same rotation speed).

When a stellar core collapses, the rotation speeds up, and the reasoning is the same as for the figure skater and the planet: If the product of axial distance and rotation speed is to remain equal because of angular momentum conservation, yet one of the factors becomes smaller (the typical distance shrinks as the stellar core collapses), then there are two possibilities: Either the core must somehow be coupled to the rest of the star, to which it then transfers huge amounts of angular momentum, or the other factor – the rotation speed – must increase.

In a typical collapse situation, there is no mechanism that would allow the transfer of sufficiently large amounts of angular momentum. In consequence, the result of the collapse will be a compact object that rotates extremely fast. One example is a neutron star, and if the collapse indeed leads to the creation of such a type of star, that star will typically rotate at some hundreds of revolutions per second. Similarly, if the collapse leads to the formation of a black hole, it will be a quickly rotating black hole. In both cases, the conservation of angular momentum is responsible.

Accretion disks

Our final example for the conservation of angular momentum is important, but significantly more complicated than its predecessors. It concerns accretion disks, rotating matter disks that form whenever the gravitational influence of a compact object – a neutron star, say, or a black hole – attracts gas or other matter from the neighbourhood. The matter orbiting the central object as part of the disk is constrained by the conservation of angular momentum: Whenever it moves inwards, towards the centre, the matter either has to transfer angular momentum to its environment, or its orbital speed needs to increase. The result is a disk in which orbital speed increases as we come closer to the central object. The innermost particles manage to transfer just enough of their angular momentum outwards to allow them to fall onto the central object’s surface (or enter the black hole).

Further Information