The fabric of space: spin networks

The quantum structure of space according to loop quantum gravity

An article by Thomas Thiemann

In Einstein’s theory of general relativity, the geometry of space and time is not fixed once and for all. Rather, it is a dynamical entity whose evolution must be determined in concert with the evolution of matter. The absence of an externally prescribed geometry is known as the principle of background independence.

Apart from general relativity, the other pillar of modern physics is quantum theory which says that the laws of nature are subject to Heisenberg’s uncertainty relation. Since matter is subject to the laws of quantum theory, since Einstein’s equations relate matter and geometry, and since this distortion of geometry corresponds, in Einstein’s theory, to gravity, it is clear that gravity must be described quantum theoretically as well.

Unfortunately, a quantum gravity theory is difficult to construct. In the construction of ordinary quantum theories (for instance quantum electrodynamics, the quantum theory of the electromagnetic field), heavy use is made of a prescribed background geometry. If a background geometry is not available, the whole structure of (ordinary) quantum theory breaks down. For instance, one of the standard ingredients of special relativistic quantum theories is the so-called causality axiom. Put simply, it says that a measurement of some properties of the quantum system can never influence another measurement made at a different time and place if such influence would have had to travel faster than the speed of light. In order to even formulate this rule, it is necessary to know how light propagates. For this, in turn, one must know what the geometry is. But if geometry is dynamical then it is impossible to know the causal structure in advance – in fact, in a typical quantum mechanical way, the causal structure itself becomes fuzzy and undetermined.

Loop quantum gravity

In order to take Einstein’s principle of background independence seriously one must generalise quantum theory. One such generalisation which leads to a candidate for a quantum gravity theory is Loop Quantum Gravity (LQG). In LQG, at each instant of time, geometry is concentrated on one dimensional structures, called graphs, which can be arbitrarily complicated. A graph is simply a network of one dimensional, oriented lines which are linked together at their end points to form a kind of mesh. The following illustration shows part of such a graph:

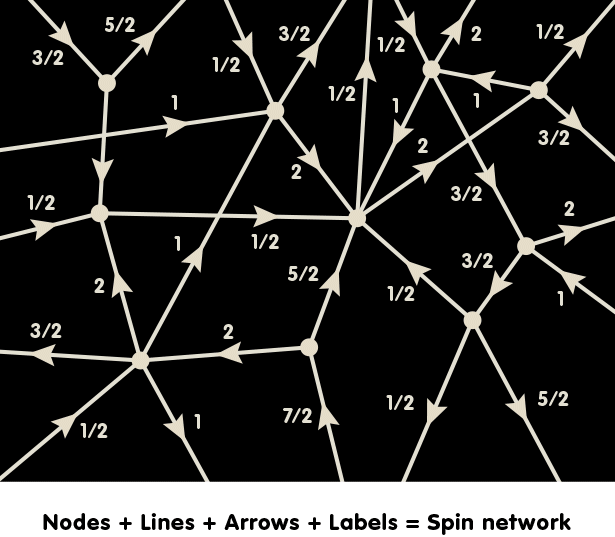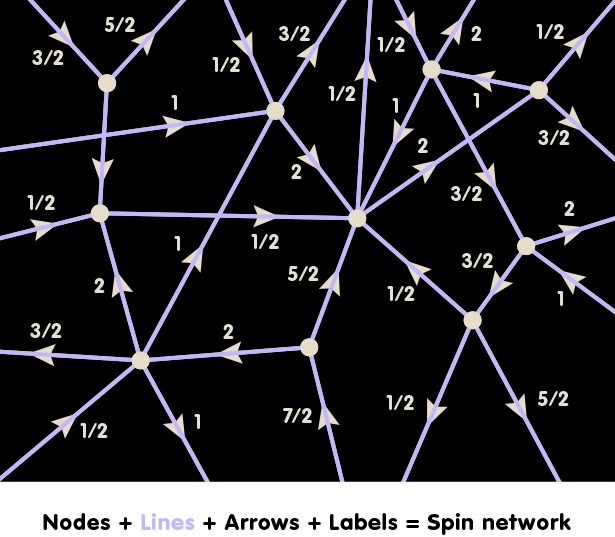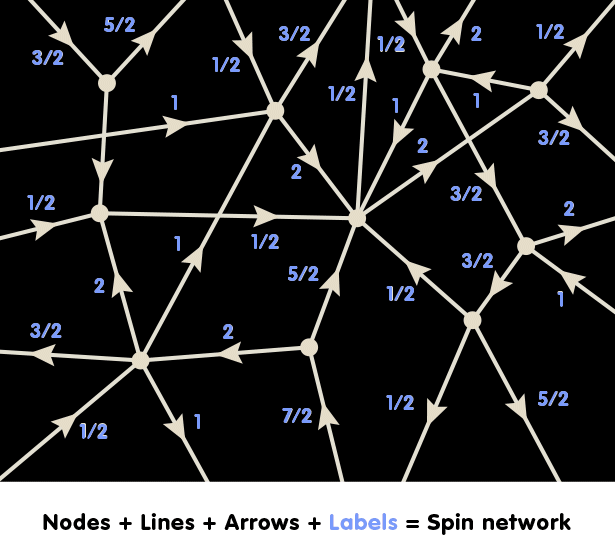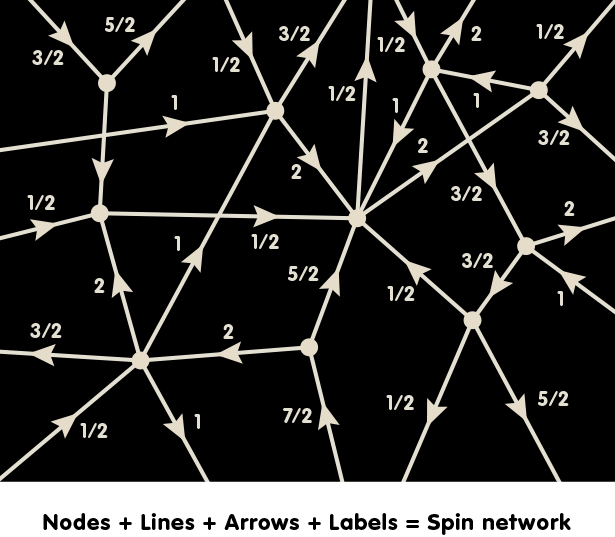
The arrows give each line a direction (in mathematics-speak, an orientation). Each line is labelled with a half-integral number. The mathematical background of this number is the same as that of spin numbers in particle physics, a type of number used to describe a basic property of elementary particles. Consequently, this number is called a spin label. (In fact, there are also labels associated with each node, but their meaning is more complicated mathematically, and we will ignore them in this simplified account.) The result is what is called a spin network, and it is taken to represent the quantum state of space at a certain point in time.

The lines do not have an a priori length – after all, there is no background geometry from which to derive lengths. Instead, we are dealing with a quantum system: In order to to talk about geometric entities like lengths or areas one must give a prescription how to measure these entities. (In technical terms, one must construct suitable operators with respect to which the spin network states are eigenstates.) In order to visualize this, it is convenient to look at graphs like the one sketched above in a different way, in what mathematicians call a dual description.

From lines to areas

Behind this is the idea that you can use a node with emerging lines – a zero-dimensional point with one-dimensional appendages – to represent a three-dimensional volume with a surface of two-dimensional faces. As a simple example, take the following node with six lines:

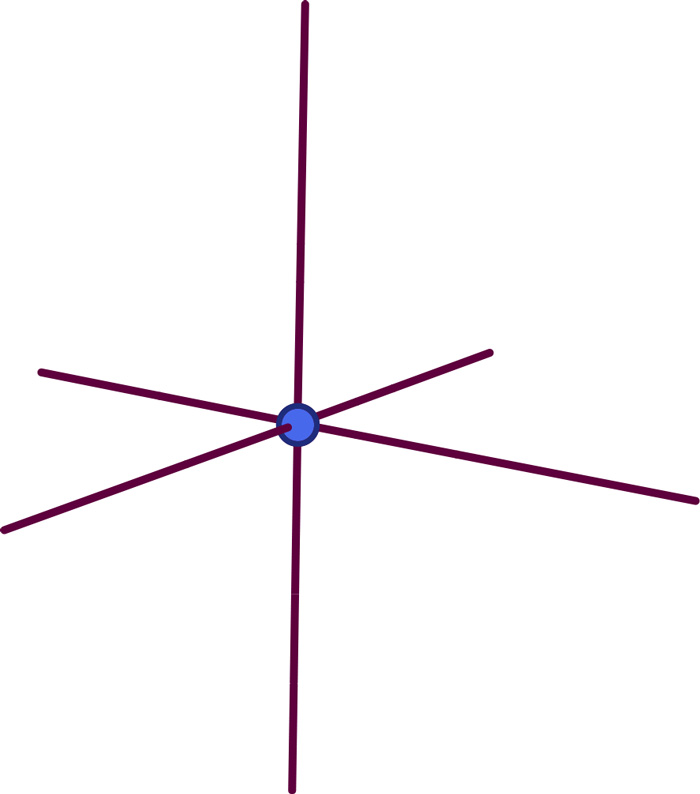
As the following picture shows, you can associate with this a solid cube-like object: The dot sits in the center of the cube, and each line represents a surface:

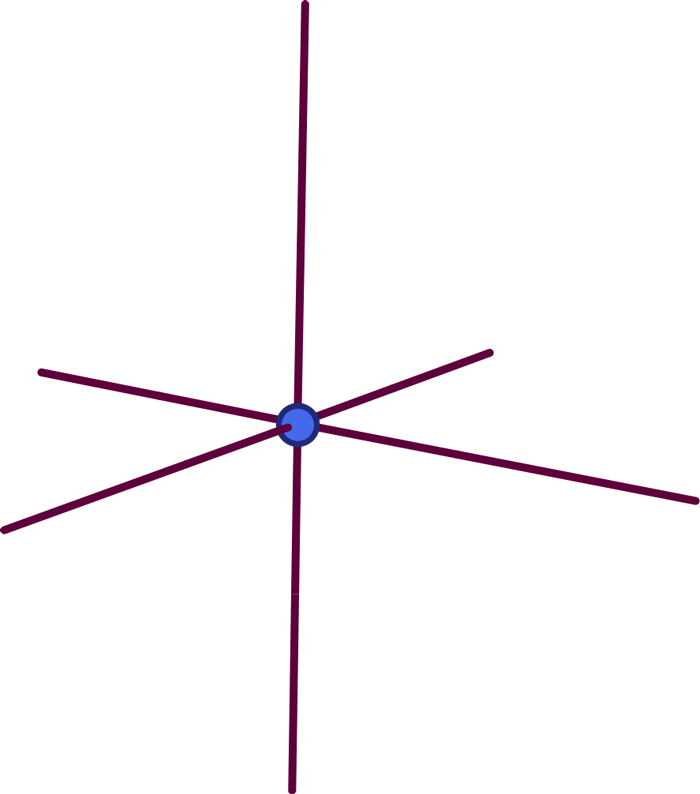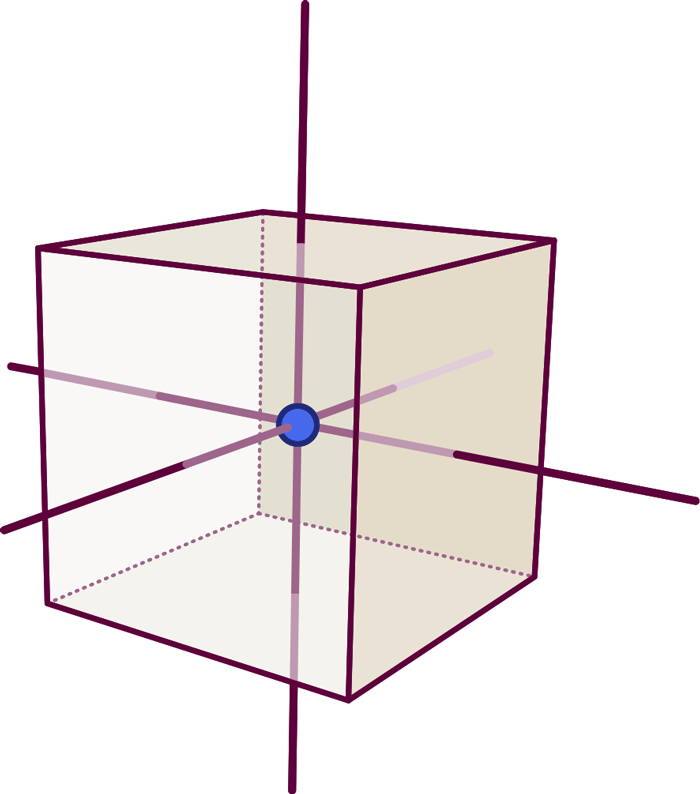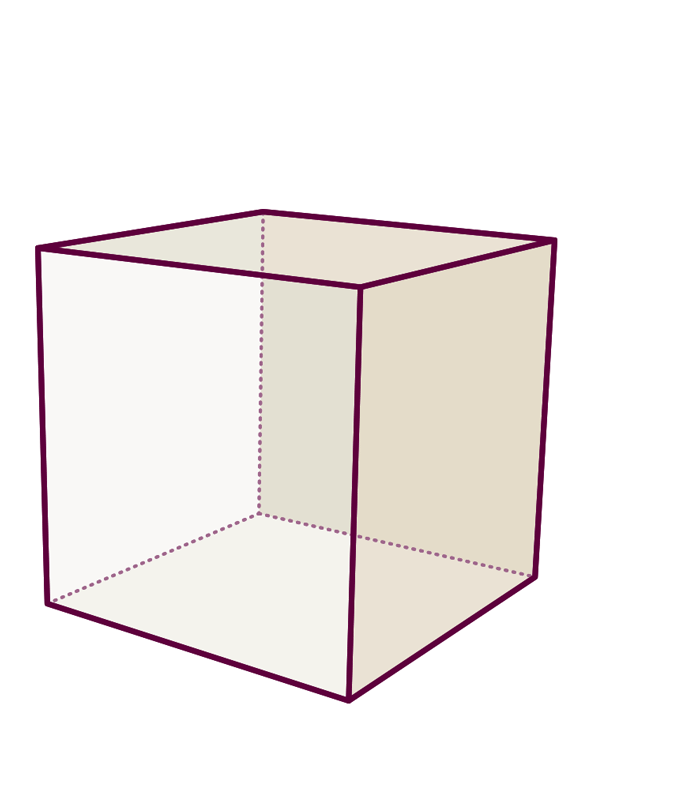
Each element of the graph is dual to (i.e. corresponds to) an element of the cube: The dot (a zero-dimensional object) represents the cube’s volume (an entity with 3-0=3 dimensions). Each line (a one-dimensional object) represents one of the faces (a surface, i.e. an object with 3-1=2 dimensions), namely the particular face pierced orthogonally by the line:

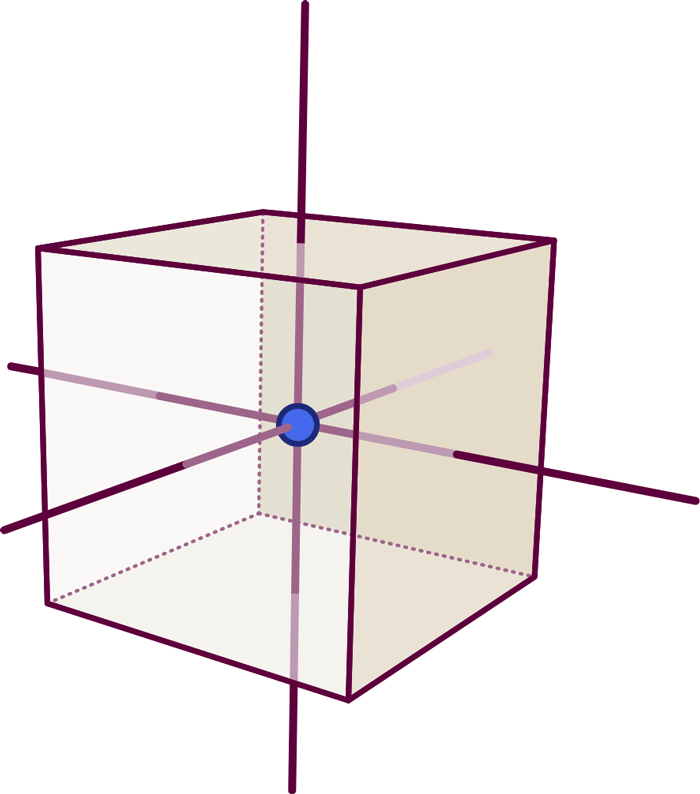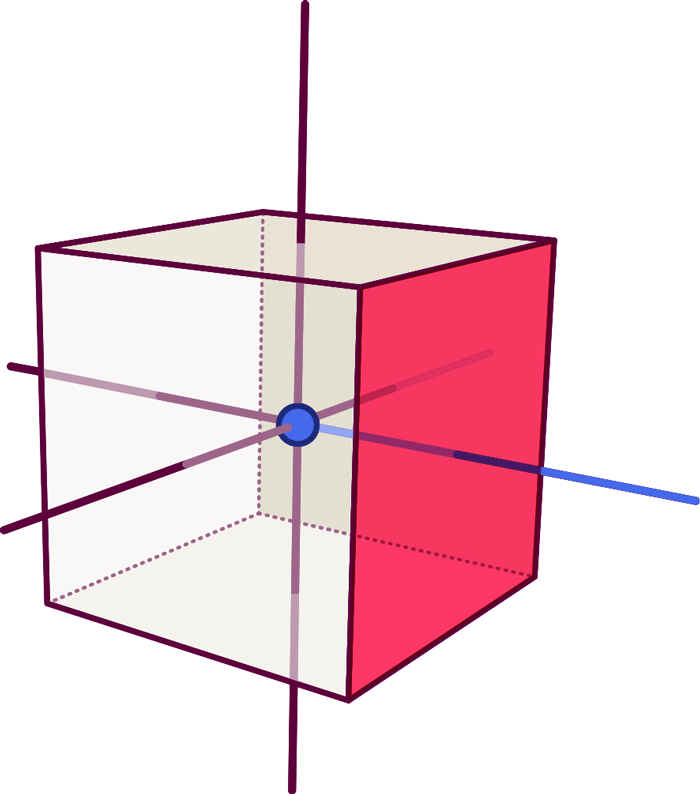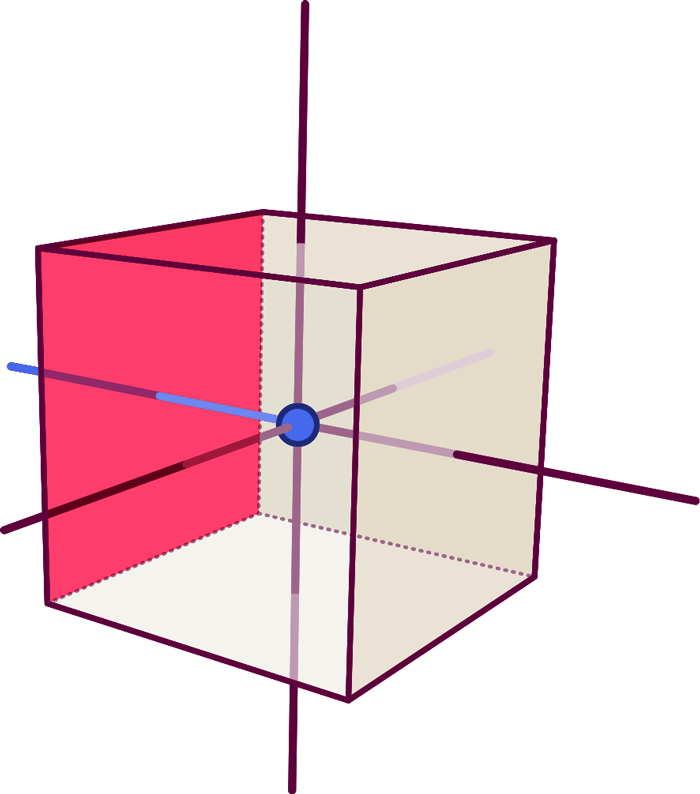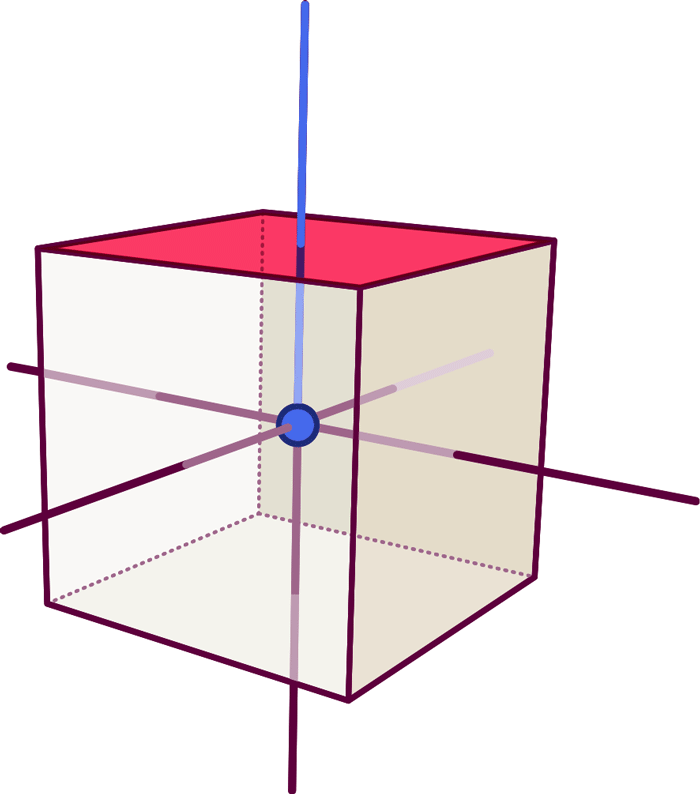
So far, this defines the dual object’s shape (in our simple case: the fact that we have six faces connected like those of a cube), but not its volume or the area of each face. We can add that extra information by labelling the graph and associating with each node a number which specifies the solid object’s volume, while each line is labelled by a number giving the surface area of the corresponding face.

Using a similar notion of duality, we can find the dual to spin-network states. After all, each such state is a labelled graph. The dual of such a graph is a connected collection of faces which intersect in one dimensional lines such that each line of the graph intersects exactly one of the faces of the complex. However, in contrast with the previous simplified example, the spin label associated with a line is not simply the numerical value of the surface area of the corresponding face. It is a more abstract number from which that area can be calculated, and for a larger spin label, a larger area results (in technical terms, a larger eigenvalue of the area operator associated with that particular face). Hence, it is still true that the label associated with a line roughly tells “how much geometry” is concentrated on the face dual to that line.

In Loop Quantum Gravity, it turns out that the areas of the faces cannot take on just any value (as they could in ordinary geometry). Instead, only a discrete set of special values is permitted. This is a typical quantum phenomenon – for instance, one of the key consequences of quantum mechanics is that the energy levels of the hydrogen atom can only take on certain discrete values. In the Loop Quantum Gravity case, the jumps between one possible value and the next are, however, extremely small – they are of the order of the Planck area of 10^-66 square centimetres (corresponding to the square of the Planck length).

In the simple example above, the cube was drawn as it would appear in ordinary space. In Loop Quantum Gravity, there is no such background structure in which the graph and its dual are embedded. In fact, it is generally impossible to represent the resulting multifaceted entity in ordinary flat, three-dimensional space in such a way that each face is pictured with its proper area. This is simply because a generic spin network will represent a space that is distorted and curved.

Flying through a spin network

In the following illustration, an artist’s conception of the dual of a spin network state, this problem is solved by expressing a face’s spin label (and thus its area value) by a colour. Thus, somewhat counterintuitively, a face can have more or less area (determined by the label) than another face even if both faces appear to have the same extension and shape in the illustration. More specifically, red means a smaller area and violet means large area. Notice that what appears as an empty region in the picture is actually no space at all: Space is only existent wherever there are faces that are excited (coloured). If we would add matter to this model, it could only exist on coloured faces (equivalently: on the lines of the spin-network). The image is a snapshot only of the dual, multifaceted entity; the actual graph underlying it is not shown for reasons of clarity:

Over time, lines of the spin network can disapppear or new lines can be created, and the value of the different spin labels can increase or decrease. One therefore could call the resulting theory Quantum Spin Dynamics (QSD) in analogy to the theory of the strong nuclear force, quantum chromodynamics. (Quantum chromodynamics defines a very similar dynamics of what is called the colour quantum numbers of elementary particles like quarks and gluons.) The details of quantum spin dynamics are such that new faces are always created or annihilated with lowest possible area (in the illustration: the red faces). The animation that can be downloaded from the following links shows an artist’s impression of this. Notice that, in the animation, the colour on the faces of the whole complex changes discontinuously while we fly through the empty space of the complex.

This chaotic foam, generated by quantum evolution, represents the properties of space deep at the Planck scale level. If we were to zoom out, it would eventually look like the smooth, continuous spacetime of ordinary, classical geometry. But wherever there are extreme concentrations of matter, corresponding to extreme curvature of space and time, a suitable physical description would need to go back to the chaotic quantum spacetime picture – for instance, to describe what happens inside a black hole or at the big bang. Much effort in Loop Quantum Gravity research is directed towards finding out what the theory has to tell us about these extreme astrophysical and cosmological situations.

 

Further Information