Gravitational redshift and White Dwarf stars
One of the fundamental effects predicted by general relativity, and some of its astronomical applications
An article by Virginia Trimble, Martin Barstow
One of the three classical tests for general relativity is the gravitational redshift of light or other forms of electromagnetic radiation. However, in contrast to the other two tests – the gravitational deflection of light and the relativistic perihelion shift –, you do not need general relativity to derive the correct prediction for the gravitational redshift. A combination of Newtonian gravity, a particle theory of light, and the weak equivalence principle (gravitating mass equals inertial mass) suffices. It is, therefore, perhaps best regarded as a test of that principle rather than as a test of general relativity.
The gravitational redshift was first measured on earth in 1960-65 by Pound, Rebka, and Snider at Harvard University, who examined gamma rays emitted and absorbed by atomic nuclei. The gravitational redshift of light coming to us from the sun has also been observed, but the accuracy is not very good because of gas motions on the solar surface: Whenever light is emitted by a moving source, there is a motion-dependent frequency shift called a Doppler shift, and in the case of the sun, the Doppler shifts due to the moving gas are somewhat larger than the gravitational redshift due to the light having to climb out of the field of the sun.
Gravitational redshift in white dwarf stars
The expected amount of redshift for light from the surface of a massive object reaching a distant observer is proportional to the object’s mass divided by its radius. This means that the stars astronomers call White Dwarfs, which are formed when low-mass stars like our sun have exhausted their nuclear fuel, are interesting candidates for observation: White dwarfs have masses close to that of the sun, but radii smaller by factors near 100. The following illustration shows the relative sizes of our sun, the earth, and a White Dwarf star. The sun is so large that we can only show some part of its disc here; the earth is the pale blue dot and the White Dwarf the pale grey dot in front of that disc:
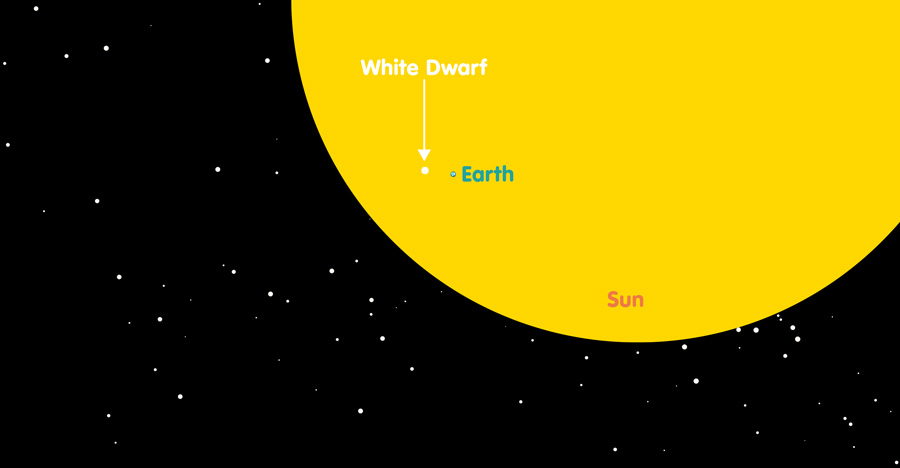
Consequently, the shift should be much larger for them than for our sun – parts in 10,000 in wavelength, rather than parts in 1,000,000. Perhaps the best known white dwarf is Sirius B, the white dwarf companion to the star Sirius you might have seen in the night sky. It is not an object visible with the naked eye, but it can be observed with telescopes – the following image was taken with the Hubble Space Telescope; Sirius B is the small object visible on the left-hand side; the cross-like structure and the small ring around Sirius B are artefacts caused by the telescope’s optical systems:

Image: NASA, ESA, H. Bond (STScI) and M. Barstow (Univ. of Leicester)
The very small radius of Sirius B was recognized in the 1920s, and several efforts were made to measure the gravitational redshift of light reaching us from Sirius B, particularly by Walter S. Adams at Mt. Wilson Observatory. Everyone liked the result he obtained, and so it was only decades later that anyone noticed or complained that about half the light he was studying was really scattered from the much brighter Sirius A.
As Sirius A and B orbit each other, their apparent separation in the night sky changes from year to year. From 1930 to 1950, the two stars were so close together in their mutual orbit that no measurement was possible. The first correct determination was probably that of Daniel M. Popper in the 1950s, and this was much improved upon by Jesse L. Greenstein and his colleagues using the 200 inch telescope on Palomar Mountain in 1970. The result agreed with general relativity (or the equivalence principle, as you prefer).
Gravitational redshifts as a tool for stellar physics
The modern reason for measuring Einstein redshifts of light from white dwarfs is to test our understanding of the structure of these burnt out cinders of stars, whose internal physics is very different from that of the sun and other normal stars. Gravitational redshift tells you the ratio of the star’s mass to its radius, M/R. There is another quantity that is measurable from stellar spectra, the surface gravity of the star (the thing that is 9.81 m/sec² on earth – the acceleration experienced by a falling body near the surface). This second quantity tells you the ratio of the object’s mass to the square of its radius, M/R². Combining the two quantities, one can extract both the object’s mass M and its radius R.
There are, however, some problems. First of all, you must know the motion of the white dwarf through space. After all, motion produces a shift in wavelength of its own, namely a Doppler shift. If you want to deduce the gravitational redshift from the measured wavelengths of the star’s light, you first need to know how these wavelengths are changed by the Doppler shift.
This problem can be solved for white dwarfs with normal binary companions (like Sirius), and for those in star clusters like the Hyades – in both cases, there is sufficient observational data to reconstruct stellar motion, and thence the Doppler shifts. Alternatively, one can evaluate the gravitational redshift statistically for a large sample of observed objects distributed over the sky. If your sample includes a sufficiently large number of stars, then some will be moving towards you, others away from you. If you compute the average observed frequency shift, then the contributions of the different Doppler effects will roughly cancel out, and you will be left with the gravitational redshift.
The second problem concerns the “spectral lines”, characteristic maxima or minima of light emission, which astronomers use to pinpoint shifts in wavelength. Ideally, spectral lines correspond to light emitted or absorbed at a single characteristic frequency – as the positions of these lines change, astronomers can measure the frequency shift. In practice, though, spectral lines are widened and cover a whole range of frequencies. Behind this are several effects, from flows in the stellar gas contributing small Doppler shifts to interaction among the gas atoms, and so forth. Because of the strong surface gravity of white dwarfs, their spectral lines are up to a hundred times more smeared out than for normal stars. With such wide lines, it is very difficult to determine exact values for the frequency shift. Further effects, such as scattering of light in the upper atmospheres of the stars, increase this difficulty. Oh, and the stars are also very faint.
Results from the white dwarf surveys
The first sample of white dwarf spectra large enough to attempt a statistical study was compiled by Greenstein at Palomar in the 1950s and 60s, for somewhat different purposes – Greenstein’s main interest at the time was the chemical composition of stars. Attempting to measure the gravitational redshift was assigned to a graduate student, Virginia Trimble, as a second year research project in 1965, partly because it was thought to be impossible.
The most important conclusion was, perhaps, that the task was possible after all. In addition, the implied masses, derived from a combination of the observed redshifts (M/R) and models for a different relationship between M and R that comes from the physics of very dense matter were in between the 0.4 solar masses of the white dwarf designated “40 Eri B” (companion of the star 40 Eridani in the constellation River Eridanus) and the 1.0 solar mass of Sirius B known from their orbits around their normal companions. And the masses for the relatively young white dwarfs in the Hyades cluster were probably somewhat larger than average. All these results are still valid today.
When astronomers give values for the gravitational redshift, they usually quote a speed value – this is simply the speed at which a body would need to recede from you to produce the same redshift by means of the Doppler effect. In the Palomar survey, the average white dwarf appeared to have a redshift near 53 km/s, corresponding to an average mass near 0.75 solar masses, while the companion of 40 Eridani showed only 23 km/s redshift, consistent with its known, smaller mass. In the 1980s, Koester, Stauffer, and Wegner all measured gravitational redshifts in additional samples of stars beyond the 80 studied by Greenstein and Trimble, finding a somewhat smaller average near 44 km/s and correspondingly smaller average mass, perhaps 0.65 solar masses.
Getting Sirius with the Hubble Space Telescope
There is no doubt that the gravitational redshift published by Greenstein and his colleagues in 1971 was a very important result. However, the difficulty of the measurement, particularly due to the proximity of Sirius A, left an uncertainty in the measured value that was too large to differentiate between alternative models of white dwarf interior structure. A further problem was the limited quality of the photographic spectra, from which other important physical parameters, the stellar temperature and surface gravity are measured. Since this pioneering work, we have entered the electronic age of optical astronomy. Modern cameras can record information with much higher sensitivity than photographic film, and the resulting data can be analysed with modern computational techniques. However, the presence of Sirius A remained a problem – that is, until the advent of modern space-based telescopes like the Hubble Space Telescope (“the Hubble”, for short)!
From its vantage point above the Earth’s atmosphere, the Hubble Space Telescope can be used to obtain sharper images than generally available from ground-based telescopes. As a result, the amount of scattered, contaminating light for Sirius A can, in principle, be dramatically reduced. However, for most of the lifetime of Hubble, Sirius B has been in an unfavourable position relative to Sirius A. Hubble was launched in 1990, and Sirius B made its closest approach (as projected on the plane of the sky) to Sirius A during 1993. Now, as the distance between the two binary companions has increased and high quality direct images of the system have been obtained with Hubble, it has become feasible to obtain an observation of Sirius B. The following figure shows two spectra that were recorded in 2004 with the Hubble’s “Space Telescope Imaging Spectrograph” (STIS):
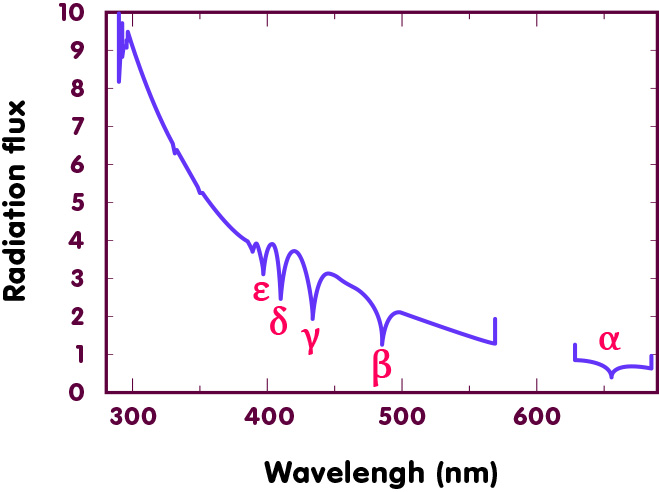
[Image after fig. 4 in Barstow et al., Mon.Not.Roy.Astron.Soc. 362 (2005) 1134-1142.]
The newly measured gravitational red-shift of 80.42 ± 4.83 km/s for Sirius B, published by Martin Barstow and colleagues, was much more accurate than before, and in good agreement with the earlier measurement, giving a mass of 0.978 ± 0.005 solar masses for the white dwarf. However, more recently, a mass measurement of 1.018 ± 0.011 solar masses obtained in 2017 by Howard Bond, from Hubble and historical ground-based observations of the orbit of the Sirius system has challenged this. The difference of 0.04 solar masses might seem small, but it is much larger than the exquisite precision of both the Hubble studies. A dynamical mass measurement is the most direct that can be made, but, equally, General Relativity is a well-established theory that has withstood many tests. Therefore, the science teams needed to look for some as yet unknown effect. A deep and detailed examination of the operation of the Hubble spectrograph revealed an unexpected uncertainty in the wavelength calibration that might give rise to a small offset in the gravitational redshift measurement. Therefore, a new set of observations was obtained with the STIS instrument on Hubble, observing both Sirius A and Sirius B in sequence to compensate for this. This latest measurement gave a redshift of 80.65 ± 0.77 km/s and mass of 1.017 ± 0.025 solar masses, in good agreement with the dynamical measurement. The corresponding white dwarf radius is 0.00808 ± 0.00011 Solar radii. This work shows that incredible precision can be achieved, which can provide a strong test of the theory of white dwarf structure.
Measurements, models, and masses
However, measurements like those obtained for Sirius B are not available for many stars. The majority of known white dwarfs are not in binary systems and estimates of their masses can only be made combining detailed examination of their spectra, which yield a value for the surface gravity M/R², with models of the interior structure of white dwarfs – the models give a relation between M and R; taken together, measurements and models allow the determination of both M and R separately. The importance of the Sirius B result is that it verifies the reliability of the models.
So what are the typical masses of white dwarfs? The Data Release 2 from the Gaia satellite contained information on about 13,000 white dwarfs within 100 parsecs of us (a nearly complete sample), and a couple hundred thousand more at larger distances. The distribution of masses includes both numbers like 0.4 solar masses and many more stars of 1.1–1.3 solar masses than were expected. The latter are probably the products of mergers. Both the small masses (because they are short-lived) and the large masses (because they are faint) were under-represented in earlier catalogues. Where there are masses from more than one method, complete agreement has not yet occurred.
Some early data analysis – which was discussed mainly online – argued for hydrogen or helium core white dwarfs. However, this is wrong: The objects have hydrogen and helium atmospheres and carbon/oxygen cores. Even more, the Gaia sample has revealed that the centers of white dwarfs crystallize as predicted many years ago by Hugh van Horn.
Further Information
For the relativistic ideas behind this spotlight topic, check out Elementary Einstein, especially the chapter on General Relativity.
Related Spotlights on relativity can be found in the section General Relativity.
This article was updated in November 2020. The original from 2010 can be downloaded here.
Colophon
is a professor of physics at the University of California, Irvine, and staff astronomer at Las Cumbres Observatory. Her research interests are the structure and evolution of stars, galaxies, and the universe, and of the communities of scientists who study them.
is a professor of astrophysics and space science at the University of Leicester. His research interests are hot white dwarfs, the interstellar medium, and the development and their observation.
Citation
Cite this article as:
Virginia Trimble, Martin Barstow, “Gravitational redshift and White Dwarf stars” in: Einstein Online Band 12 (2020), 12-1005