The shape of space
The different space geometries allowed by the big bang models – do we live on a hypersphere?
An article by Markus Pössel
In three-dimensional space as we know it, geometry is governed, in excellent approximation, by the laws of Euclidean geometry, the standard geometry taught in high school. For instance, all the angles within a triangle always add up to 180 degrees, and parallel lines never intersect.
However, according to the big bang models – the cosmological models based on general relativity, ideally suited for universes like ours that are, on the whole, homogeneous – this is not the only possibility. In those models, space geometry depends on the energy and mass content of the universe, more precisely: on its average density. With the universe continually expanding, that average density is continually getting smaller, and in order to compare different densities, it is necessary to choose a reference time. Cosmologists choose “now” as such a reference time – in view of the billion of years that separate us from the zero point of cosmic time, the few decades that “now” changes in the course of cosmological research do not matter. For the present universe, the big bang models predict a certain critical density, connected with the geometry of space.
Hyperbolic geometry
If the current density of the universe is below the critical value, then the geometry of our universe is analogous to that of a saddle. The two-dimensional version of such a geometry is shown below:
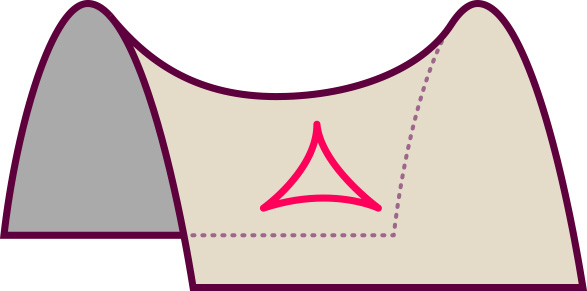
In such a space, the angles of a triangle built from segments of straightest-possible lines (geodesics) always sum up to less than 180 degrees, and if you follow some straightest-possible lines that are parallel in some region of space, they will always diverge. In the language of mathematics, this is called a space of negative curvature.
Flat geometry
On the other hand, if the current density of the universe is exactly equal to the critical density, then every region of space has the usual, Euclidean geometry we know and love:

In such a space, as I already mentioned, the angles in a triangle add up to exactly 180 degrees, and if you follow some straightest-possible lines (which, in this special case, are simply straight lines) that are parallel in some region of space, they will remain parallel. This is called a space of zero curvature or, equivalently, a flat space.
Spherical geometry
The final possibility: If current density is larger than the critical value, then every region of space has a geometry akin to that of a sphere. Here, again, is the two-dimensional example, a spherical surface:
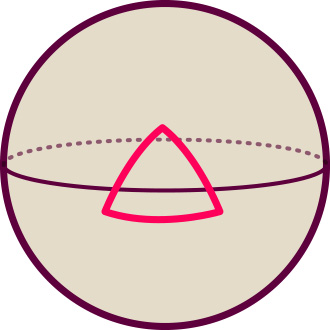
In such a space, the angles of a triangle built from segments of straightest-possible lines (geodesics) always sum up to more than 180 degrees, and if you follow some straightest-possible lines that are parallel in some region of space, they will always converge and intersect. This is called a space of positive curvature.
Interesting possibilities for large-scale geometry, and the mathematically inclined reader will react with slight regret to the announcement that, going by astronomical data, the most boring among these possibilities is realized: The geometry of our universe at cosmic scales appears to be that of ordinary high school geometry, corresponding to a universe with a density equal to the critical value.
Further Information
For the relativistic ideas at the basis of this spotlight topic, check out Elementary Einstein, especially the chapter Cosmology.
Related Spotlights on relativity can be found in the section Cosmology.
Colophon
is the managing scientist at Haus der Astronomie, the Center for Astronomy Education and Outreach in Heidelberg, and senior outreach scientist at the Max Planck Institute for Astronomy. He initiated Einstein Online.
Citation
Cite this article as:
Markus Pössel, “The shape of space” in: Einstein Online Band 04 (2010), 01-1021










