Twins on the road
How one can picture the situation of the travelling twin, using a simple geometric analogy
An article by Markus Pössel
The curious case of the twins: One of them hops into a spaceship and flies away into space at nearly light speed before returning to Earth. As they meet again, the travelling twin is markedly younger than the one that stayed on Earth. A dramatic, if hypothetical example for one of the fundamental consequences of special relativity: How fast or slow time passes depends on how you move.
Can the travelling twin simply turn the tables? Declare himself as having been at rest, while the Earth has first moved away and then returned? Which is why the twin on Earth should be the younger one now? No way, since there’s an indisputable difference between the twins allowing us to tell which is the travelling one: The space-travelling twin, in turning around to head back to Earth, has experienced acceleration , either when slowing down and then re-accelerating towards Earth, or in turning his spaceship around in order to head home, while the stay-at-home twin hasn’t. (More about this can be found in the spotlight topic The case of the travelling twins.)
But how does this work – why is the acceleration so important? Did the travelling twin stay young because time went especially slowly for him during the acceleration phase?
Not at all. In order to get a clearer picture, consider the following analogy that is not about time intervals, but about distances in space.
The case of the two hikers
Take two hikers, Albert and Emmy, both hiking from location A to location B. Emmy takes the straight road linking A and B. Albert makes a detour via location C, taking a straight road from A to C and then another from C to B. The following illustration shows Albert’s and Emmy’s routes:
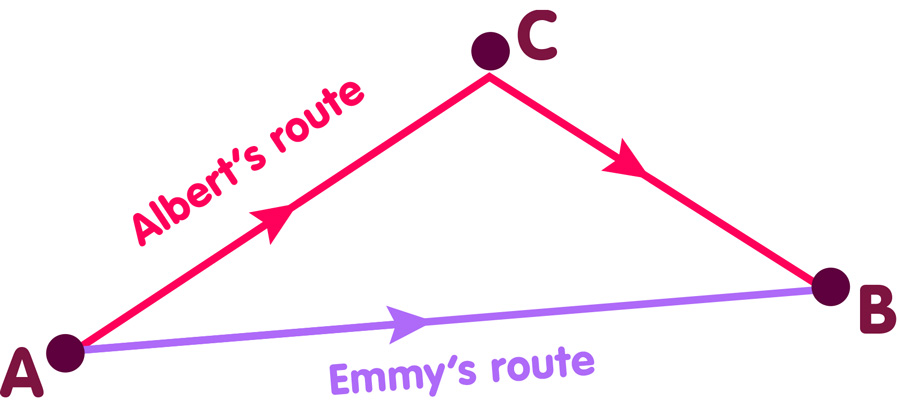
When the hikers meet again at location B, Albert has evidently covered more distance than Emmy. This is directly connected to the fact that, while both have been walking along straight roads, there is a point where Albert has changed direction, while Emmy has not changed her direction at all.
Is the additional distance somehow “concentrated” at point C, where Albert has changed direction – would a pedometer (that counts Albert’s steps, and thus measures the distance covered) suddenly run mad and register many additional steps when Albert turns the corner? An absurd notion. The change-of-direction is no secret reservoir of additional distance. It is a joint: An element that is needed to connect two straight roads in such a way that they lead from A to B, where the distance from A to B is shorter than the combined length of the two connected roads.
Back to the twins
This brings us back to the twins in special relativity. We will consider only the simplest version: The travelling twin travels at constant speed away from Earth, then fires up his rocket engines to decelerate and subsequently accelerate back in the direction of Earth before cutting his engine and flying, again with constant speed, towards his rendezvous with the twin that stayed at home.
The different distances travelled by the two hikers in our example correspond to the different times that pass on the twins’ clocks between the launch and the return of the travelling twin’s spaceship. There is only one odd and unfamiliar feature to the analogy: Longer distances for the hikers correspond to shorter time intervals for the twins. There’s no way to see this without digging a bit deeper, but it follows directly from the formulae of special relativity, and it is true whenever one constructs analogies between space (where there are only space dimensions) and spacetime (where there are three space dimension and one time dimension).
Albert’s two stretches of straight road from A to C and from C to B correspond to the travelling twin moving at a constant speed away from, and later back towards Earth. The acceleration (change in velocity) felt by the travelling twin corresponds to Albert’s turning the corner (his change in direction). A more complicated travel route for the travelling twin, with lots of accelerations and decelerations, would correspond to Albert taking a curved, meandering path from A to B.
(If so inclined, one can take the analogy even further, define an analogue of simultaneity and even derive relativistic time dilation. Interested? Then consult the spotlight topic Time dilation on the road!)
The role of acceleration
This analogy between the role played by acceleration in the case of the travelling twins and the role of the triangle edge at C is, in fact, very close to the more precise mathematical description in special relativity. The crucial point is not that clocks run especially slowly during the acceleration phase – that’s not what is behind the twin’s age difference, just as the additional distance covered by Albert’s route isn’t concentrated at the point where he changes direction.
Acceleration plays the same role as a joint, an element that is of crucial importance when you want to connect two straight pieces together so as to join A with B, when the combined length of these two pieces is not the same as the distance from A to B. The distance is in the pieces, not in the joint. In the geometrical language of spacetime, acceleration is exactly such a joint, something that is needed to form a spacetime triangle in which the sum of the time intervals for two separate pieces that we want to combine to stretch from A to B is smaller than the time interval for a direct connection from A to B.
A is the start of the space-ship, B its return. The two time intervals we want to connect are those elapsing on the travelling twin’s clock as he flies at constant speed away and towards Earth, respectively. The time interval for the direct connection of A and B is that which elapses on the clock of the twin that stayed at home. The twin has stayed younger not because of any direct influence of acceleration on clocks. The time he has aged is the sum of the time intervals that have elapsed during the two legs of his journey. But in order for those two legs to bring him back to Earth, in order for them to fit together in exactly the right way, we need a joint between them – an acceleration phase.
Further Information
The basics of special relativity – which is the framework for the case of the travelling twins and for this analogy – can be found in Elementary Einstein in the section Special Relativity.
Related Spotlight topics on Einstein-Online an be found in the section Special Relativity.
Colophon
is the managing scientist at Haus der Astronomie, the Center for Astronomy Education and Outreach in Heidelberg, and senior outreach scientist at the Max Planck Institute for Astronomy. He initiated Einstein Online.
Citation
Cite this article as:
Markus Pössel, “Twins on the road” in: Einstein Online Band 04 (2010), 01-1008