The Singularity Theorem (Nobel Prize in Physics 2020)
In 2020, Roger Penrose was awarded half of the Nobel prize in physics for proving that black hole formation is a robust prediction of Einstein’s general theory of relativity.
An article by Emanuel Malek
The British physicist and mathematician Roger Penrose shared one half of the Nobel Prize in Physics 2020 for his discovery that black hole formation is a robust prediction of the general theory of relativity.
Since its formulation in 1916, Einstein’s theory of general relativity has repeatedly surprised and confounded physicists. For example, in general relativity, space and time are not absolute and fixed, but instead they are mixed and warped by the presence of matter and energy. According to Einstein’s theory, this warping of spacetime leads to the gravitational force. By the 1960s most physicists had come to terms with many of the revolutionary features of general relativity. However, one of the strangest predictions of general relativity, the existence of black holes, was still hotly debated.
The end of spacetime
The mathematical equations governing general relativity allow for solutions where matter is so densely packed into a small region of spacetime that nothing, not even light, can escape from this region, called a black hole. The black hole is separated from the rest of spacetime by an event horizon, a point of no return. According to general relativity, anything that crosses the event horizon, will never escape and inevitably fall into the center of the black hole.
What makes black holes even more troublesome for physicists is that deep inside the black hole a singularity exists and any object that falls into the black hole will eventually reach this singularity. At the singularity, the gravitational field becomes infinitely strong and rips apart spacetime itself. Therefore, according to the mathematics governing general relativity, any object that reaches the singularity will cease to exist – a very problematic consequence for the physical world.
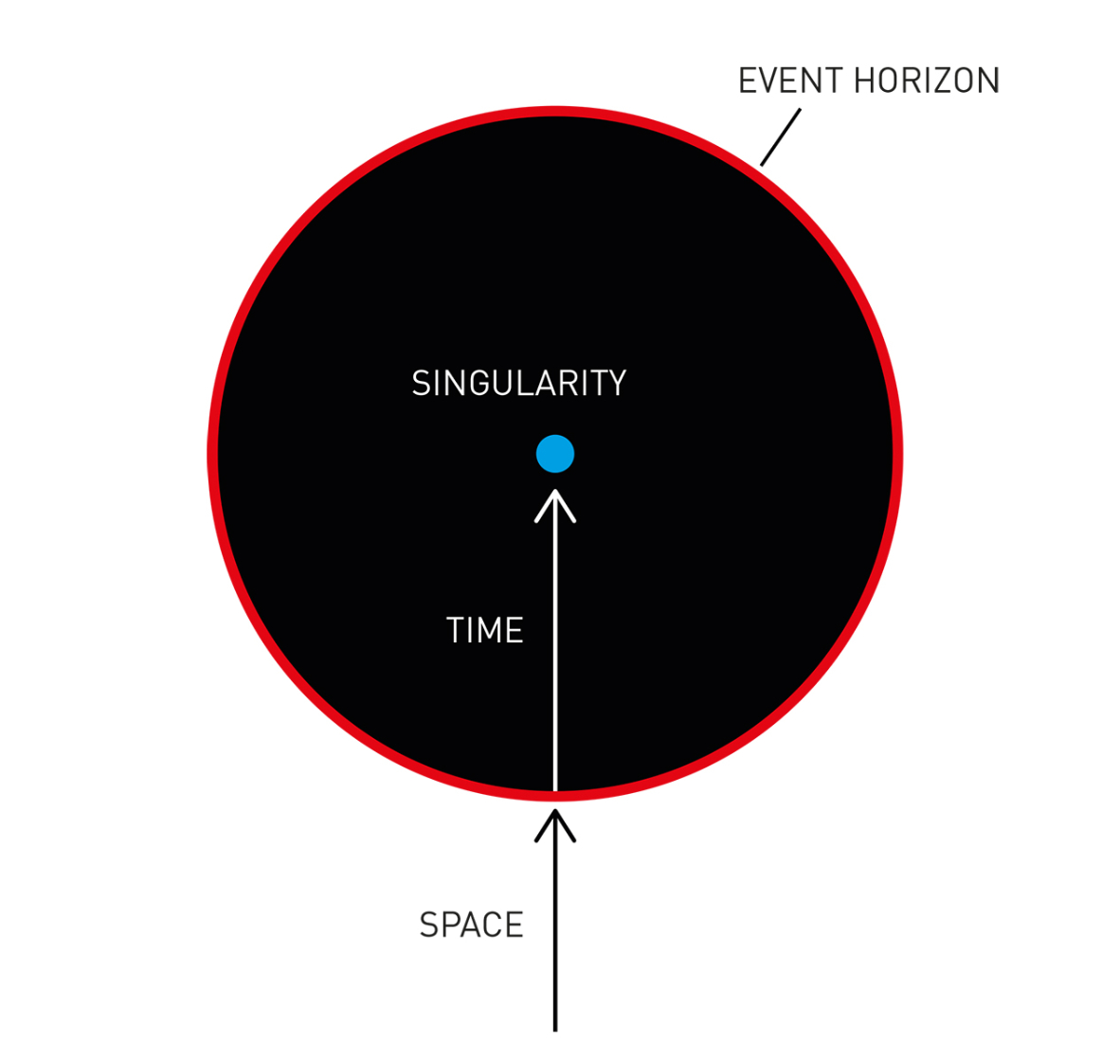
Illustration of a black hole and the singularity on its inside. ©Johan Jarnestad/The Royal Swedish Academy of Sciences
Mathematical artifact or physical prediction
This pathological nature of the singularity, the fact that space and time will cease to exist there, is extremely worrying for general relativity. However, until Penrose’s work, it was unclear whether black holes and singularities can even exist in nature or whether they are just a mathematical artifact of the theory. In fact, all black hole solutions known by this point required a perfect symmetrical arrangement, which is impossible to achieve in nature.
Many physicists therefore long believed that black holes do not form in the real world. Consider how a black hole would form in nature. It requires enough matter and energy to be placed into a limited region of spacetime such that the gravitational force overcomes any pressure or other repulsive forces to trigger gravitational collapse, where the gravitational force becomes so dominant that all matter would be squeezed into an ever smaller space until a black hole forms. While such a theoretical process of gravitational collapse into a black hole was described already in 1939 by Robert Oppenheimer and Hartland Sweet Snyder, they assumed that the matter was made of an idealized dust, which exerted no pressure, and was arranged in a perfectly spherically symmetric manner. However, these ideal conditions will never be encountered in nature.
Could it therefore be that the smallest perturbation from spherical symmetry, or the smallest amount of pressure, will stop the formation of the black hole? One could argue that with a small perturbation, the matter may no longer collapse all onto the same point but instead the matter may overshoot. Moreover, perhaps even a small amount of pressure could stop the formation of a singularity. The complicated nature of the equations governing general relativity and the lack of modern computing power made this question difficult to answer.
Penrose’s singularity theorem
Penrose proved that singularities – and by extension black holes – form generically in general relativity, without stringent symmetry assumptions and for general properties of the matter. Penrose’s key insight was to focus on how the gravitational force affects light. In general relativity, gravity exerts a force on light and causes it to deviate it from its otherwise straight path. Therefore, a heavy object will cause the gravitational lensing of light passing by it. Much like an optical lens, the gravitational force causes the light to converge onto a focal point.
When the gravitational force is strong enough, the gravitational lensing effect can cause a trapped surface in spacetime. This is a 2-dimensional closed surface, like a sphere, such that all light rays perpendicular to the surface converge. This contrasts with a spherical surface in flat spacetime, where outward-directed light rays will diverge. Put differently, no light can escape the trapped surface due to the gravitational effect.
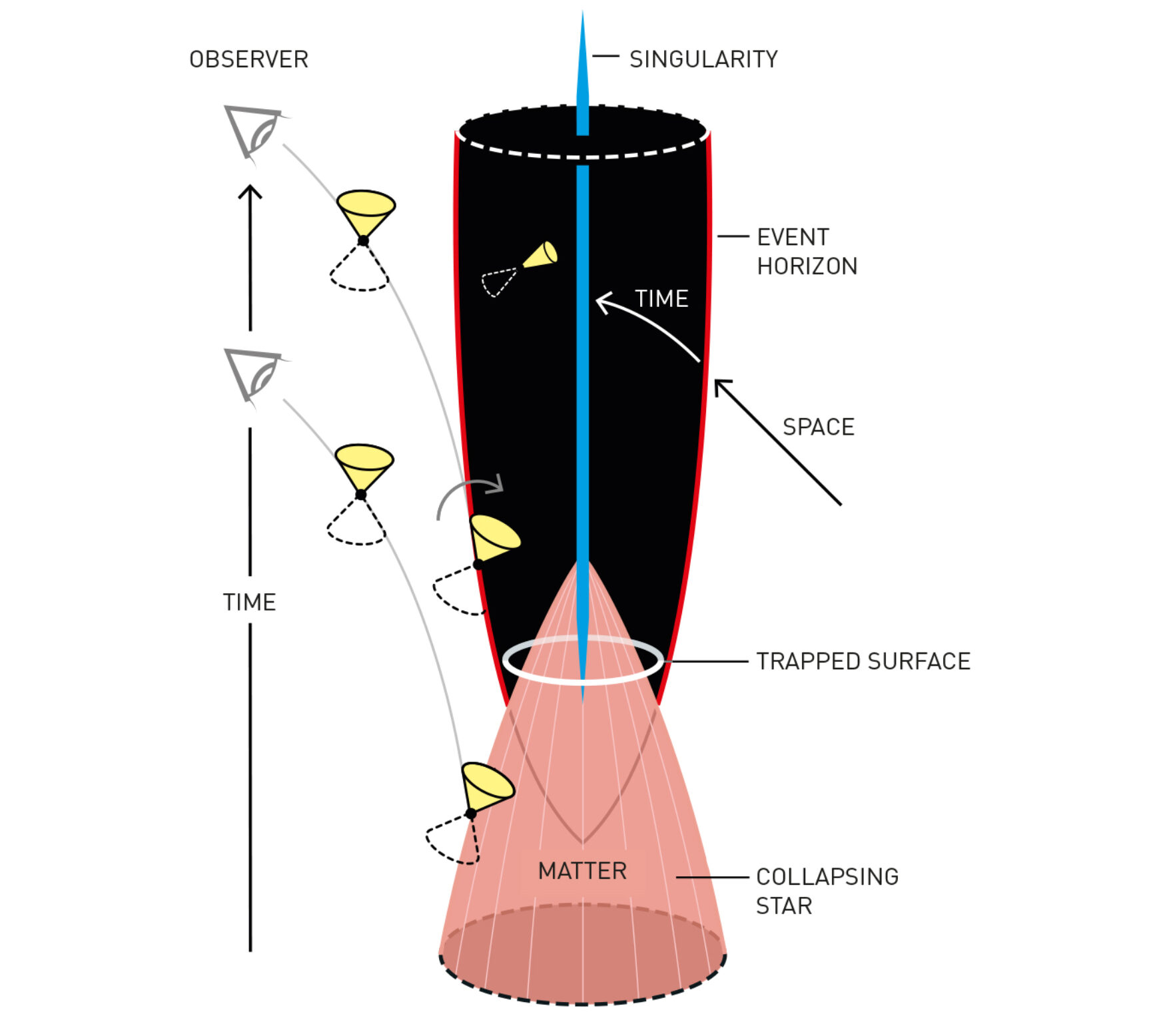
Illustration based on Penrose’s diagram showing gravitational collapse and formation of a singularity in a trapped surface ©Johan Jarnestad/The Royal Swedish Academy of Sciences
Penrose showed that, if all matter has a positive energy-density, known as the weak energy condition, a trapped surface necessarily implies that the spacetime contains a singularity. Therefore, with minimal assumptions on the matter contained in the spacetime, Penrose concluded that once a trapped surface occurs, the formation of a spacetime singularity is inevitable. This also implies that singularities arise generically in general relativity, even without special symmetries. For example, in the spherically symmetric collapse scenario of Oppenheimer and Snyder, there is a trapped surface which persists even when the spherical arrangement of matter is perturbed.
The nature of the spacetime singularity
The power of Penrose’s argument rests in its minimal assumptions, which only require the existence of a trapped surface and the weak energy condition. As a result, the singularity theorem applies very broadly and shows that singularities arise in many situations in general relativity. However, because Penrose’s argument is so general, it also does not give us any information about the singularity, beyond its existence. In fact, Penrose’s argument does not show that there must be an event horizon, and thus a black hole, surrounding the singularity.
In some ways, Penrose’s singularity theorem has made general relativity even more pathological. It has shown that singularities are a robust prediction of general relativity and need not even be hidden inside black holes. Therefore, it seems as if spacetime will quite generally have holes in it, where space and time end and the laws of physics lose applicability: naked singularities.
To counter this preposterous setup, Penrose formulated the weak cosmic censorship conjecture, which states that all singularities in spacetime must be hidden behind an event horizon. This would protect the rest of spacetime from the disastrous consequences of the singularity by a black hole’s event horizon. While this statement is widely believed to be true, it has proven remarkably difficult to prove and continues to be an active area of research. One problem is that it is hard to formalize the conjecture in a way that can be (dis)proven without immediately running into counterexamples.
The Big Bang singularity and quantum gravity
Penrose’s singularity theorem spurred on many developments in general relativity. For example, together with Hawking, Penrose generalized his singularity theorem in order to apply it to the universe as a whole. As a result, they were able to show that our universe must itself contain a singularity deep in its past, from which all matter and energy emanated in a Big Bang.
The fact that singularities arise generically in Einstein’s theory of general relativity has further spurred on the quest for a theory of quantum gravity, such as string theory. Such a quantum gravity theory would supersede Einstein’s theory on small enough scales in a way that is compatible with quantum mechanics. It is hoped that this theory would also cure spacetime singularities that currently plague the insides of black holes.
Further Information
Learn more about general relativity and black holes in our elementary tour or read the spotlights on singularities and gravitational lensing.
Find all nobel prizes related to Einstein’s theories in our spotlight Einstein’s Nobel heritage.
Colophon
Emanuel Malek is a theoretical physicst, working on various aspects of string theory, at Humboldt University Berlin.
Citation
Cite this article as:
Emanuel Malek, “The Singularity Theorem (Nobel Prize in Physics 2020)” in: Einstein Online Band 12 (2020), 12-1004