Wie viele verschiedene Arten von Schwarzen Löchern gibt es?
Langfristig gesehen gibt es nur einige wenige Arten von Schwarzen Löchern – dieser Text erklärt, welche, und wie es zu der Vereinfachung kommt
Ein Artikel von Piotr Chrusciel
Wenn ein Himmelsobjekt zu einem Schwarzen Loch kollabiert, ist dies typischerweise ein hochdynamischer, komplizierter Vorgang. Doch was ist, wenn der Kollaps beendet ist, der Staub sich gelegt und die Lage sich beruhigt hat? Wieviele verschiedene mögliche Endzustände gibt es – wieviele verschiedene Arten Schwarzer Löcher?
Wie viele Arten Schwarzer Löcher gibt es?
Mit dieser Frage beschäftigen sich die so genannten Eindeutigkeitssätze für Schwarze Löcher. Selbst dann, wenn wir uns auf die Arten von Materie und Wechselwirkungen beschränken, die für die Astrophysik eine Rolle spielen (die einzigen Wechselwirkungen mit langer Reichweite sind dann Elektromagnetismus und Gravitation) und exotischere Szenarien beiseite lassen, könnte man meinen, es gebe immer noch eine unübersichtliche Vielzahl Schwarzer Löcher. Schließlich könnte es genau so viele Arten Schwarzer Löcher geben, wie es kollabierende Objekte gibt: Ein kollabierender Materiewürfel würde zu einem würfelförmigen Schwarzen Loch, eine kollabierende Zigarre zu einem zigarrenförmigen Loch, und so weiter, wie in der folgenden Abbildung angedeutet:
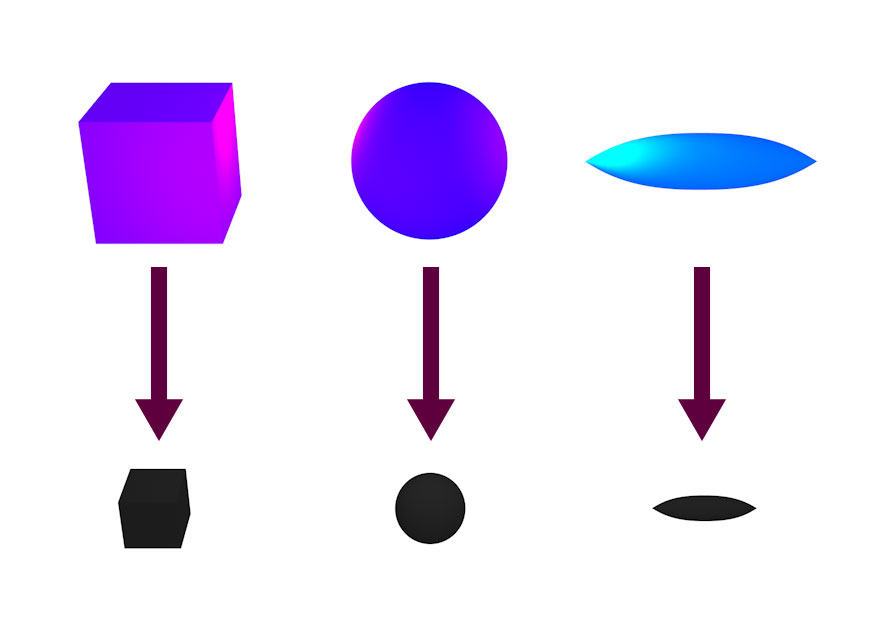
Tatsächlich stellt sich heraus, dass Schwarze Löcher zumindest auf lange Sicht deutlich einfacher sind. Bereits ein paar wenige Parameter reichen aus, um ein Schwarzes Loch komplett zu charakterisieren: Gesamtenergie, Drehimpuls (grob gesprochen: wie schnell das Schwarze Loch rotiert) und (für astrophysikalische Szenarien in der Regel weniger wichtig) elektrische Ladung. Liegen diese Parameter fest, dann ist das Schwarze Loch – genauer, die Art und Weise in der die Raumzeit rund um das Schwarze Loch herum verzerrt ist – bereits festgelegt. Kugel, Würfel oder Zigarre – sie alle kollabieren zu einem Schwarzen Loch, das keinerlei Spuren seiner ursprünglichen Form mehr aufweist:
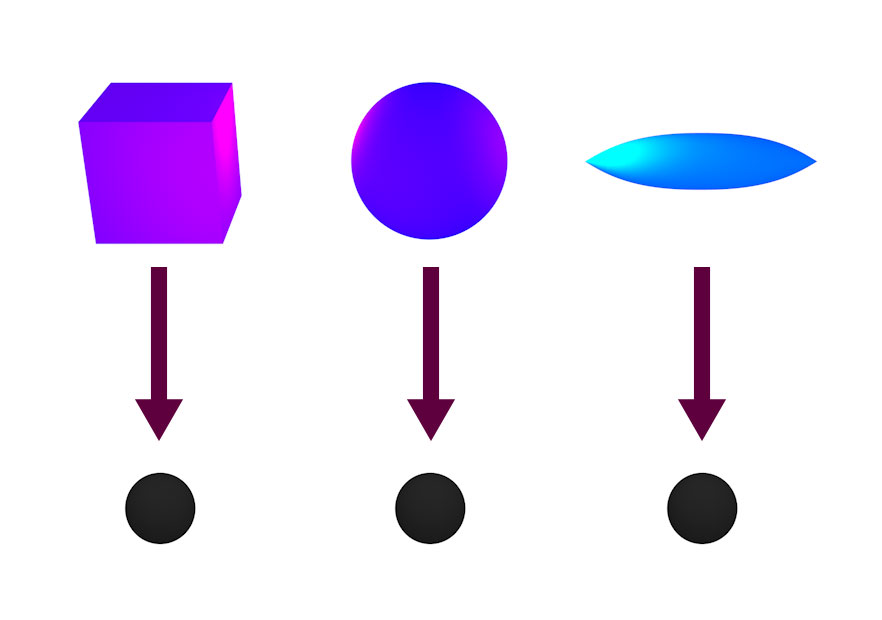
John Wheeler hat für diese überraschende Eigenschaft Schwarzer Löcher die Kurzformel „Schwarze Löcher haben keine Haare“ bekannt gemacht (erfunden von einem unbekannten Zuhörer in einer von Wheelers Vorlesungen). Das entsprechende Theorem heißt analog das „Keine-Haare-Theorem“ oder auch, im deutschen, der „Glatzensatz“. Diese Bezeichnungen bringen zum Ausdruck, dass Schwarze Löcher bereits durch die erwähnten wenigen Parameter vollständig beschrieben werden – über die Werte dieser Parameter hinaus haben Schwarze Löcher keine individuellen Kennzeichen (keine „Frisuren“).
Wie verlieren Schwarze Löcher ihre Haare?
Doch wie kommt es dazu – wie entsteht bei einem komplizierten Kollapsvorgang ein einfaches Schwarzes Loch? Wie entledigt sich ein zigarrenförmiges Objekt beim Zusammenstürzen aller zigarrenartigen Eigenschaften? Im Rahmen der allgemeinen Relativitätstheorie gibt es einen natürlichen Mechanismus dafür, kompliziertere geometrische Strukturen einer bestimmten Raumregion zu vereinfachen: Die Abstrahlung von Gravitationswellen, durch die kompliziertere Verwerfungen der Geometrie davongetragen werden können – wobei die Gravitationswellen entweder in die Tiefen des Weltraums entkommen oder aber von dem Schwarzen Loch verschluckt werden.
Die Gravitationswellen können dabei eine ganze Reihe von Eigenschaften davontragen, aber nicht alle. Elektrische Ladung können sie beispielsweise überhaupt nicht transportieren, da Gravitationswellen (ebenso wie elektromagnetische Wellen) keine elektrische Ladung besitzen. Subtilere Einschränkungen gibt es bei der Frage, wieviel an Drehmoment und wieviel an Masse (beides Größen, für die so genannte Erhaltungssätze gelten) in Form von Gravitationswellen abgestrahlt werden kann.
Von diesen Einschränkungen abgesehen gehorchen die Gravitationswellen der Grundregel aus T.H. Whites Roman Der König auf Camelot (The Once and Future King), „Alles, was nicht verboten ist, ist zwingend vorgeschrieben“: In Form von Gravitationswellen strahlt das entstehende Schwarze Loch alles ab, was es nur irgend abstrahlen kann. Das ist der Grund, warum das Endstadium nur noch durch das absolute Minimum an Parametern gekennzeichnet ist, entsprechend physikalischen Größen, die gar nicht oder nur eingeschränkt abgestrahlt werden können: Gesamtenergie (beziehungsweise, äquivalent dazu, die Masse), Drehimpuls und elektrische Ladung.
Galerie der einfachen Schwarzen Löcher
Wie also sehen die einfachen Schwarzen Löcher aus? Genauer, die einfachen stationären Schwarzen Löcher, jene nämlich, die ihre stürmische Entstehungsgeschichte hinter sich gelassen und einen langfristig unveränderlichen Zustand erreicht haben?
Beginnen wir mit den Vakuum-Schwarzen Löchern – Schwarzen Löchern in einer Umgebung, die komplett leer und frei von aller Materie ist.
Die einfachsten stationären Vakuum-Schwarzen Löcher sind die kugelsymmetrischen. Ein von J. T. Jebsen bereits 1921 bewiesenes Theorem (heute mit dem Namen von George D. Birkhoff verknüpft, der es im Jahre 1923 unabhängig von Jebsen wiederentdeckte) zeigt, dass alle kugelsymmetrischen Schwarzen Löcher stationär sind und zu einer Familie von Lösungen der Einstein-Gleichungen gehören, die der Astrophysiker Karl Schwarzschild im Jahre 1916 gefunden hat. Die Vertreter dieser Familie unterscheiden sich bezüglich des Wertes eines einzigen positiven Parameters m, der die Masse des Schwarzen Lochs angibt:

Die Schwarzschild-Lösung ist ein Spezialfall einer Familie von Lösungen, die Roy Kerr im Jahre 1963 niedergeschrieben hat, und die den allgemeinsten Fall eines stationären Vakuum-Schwarzen Loches beschreiben. Jedes Mitglied der Familie wird durch die Werte von zwei Parametern charakterisiert, die Masse m und den Drehimpuls J:

Setzt man bei einem Kerr-Loch den Drehimpulsparameter J auf Null – entsprechend einem nichtrotierenden Schwarzen Loch – dann ist das Ergebnis einmal mehr ein Schwarzschild-Loch der entsprechenden Masse.
Der Beweis, dass dies in der Tat alle Vakuum-Schwarzen Löcher sind, hat eine lange Geschichte. Die ersten Beweisschritte fand Werner Israel im Jahre 1967; zusätzliche Beiträge stammen von Brandon Carter, Stephen Hawking und einer Reihe weiterer Forscher.
Als nächstes können wir Schwarze Löcher betrachten, die elektrisch geladen sind. Dies sind keine Vakuum-Schwarzen Löcher mehr, da der umgebende Raum in diesem Falle mit einem elektrischen Feld angefüllt ist. Im Kontext der allgemeinen Relativitätstheorie sind solche Felder eine Art von Materie – die mit ihnen assoziierte Energie ist eine Gravitationsquelle.
Stationäre, elektrisch geladene Schwarze Löcher werden durch eine Familie von Lösungen der Einstein-Gleichungen beschrieben, die Roy Kerr und Ted Newman unabhängig voneinander im Jahre 1963 gefunden haben. Solche Schwarzen Löcher sind durch ihre Masse m, ihren Drehimpuls J und ihre elektrische Ladung Q charakterisiert:
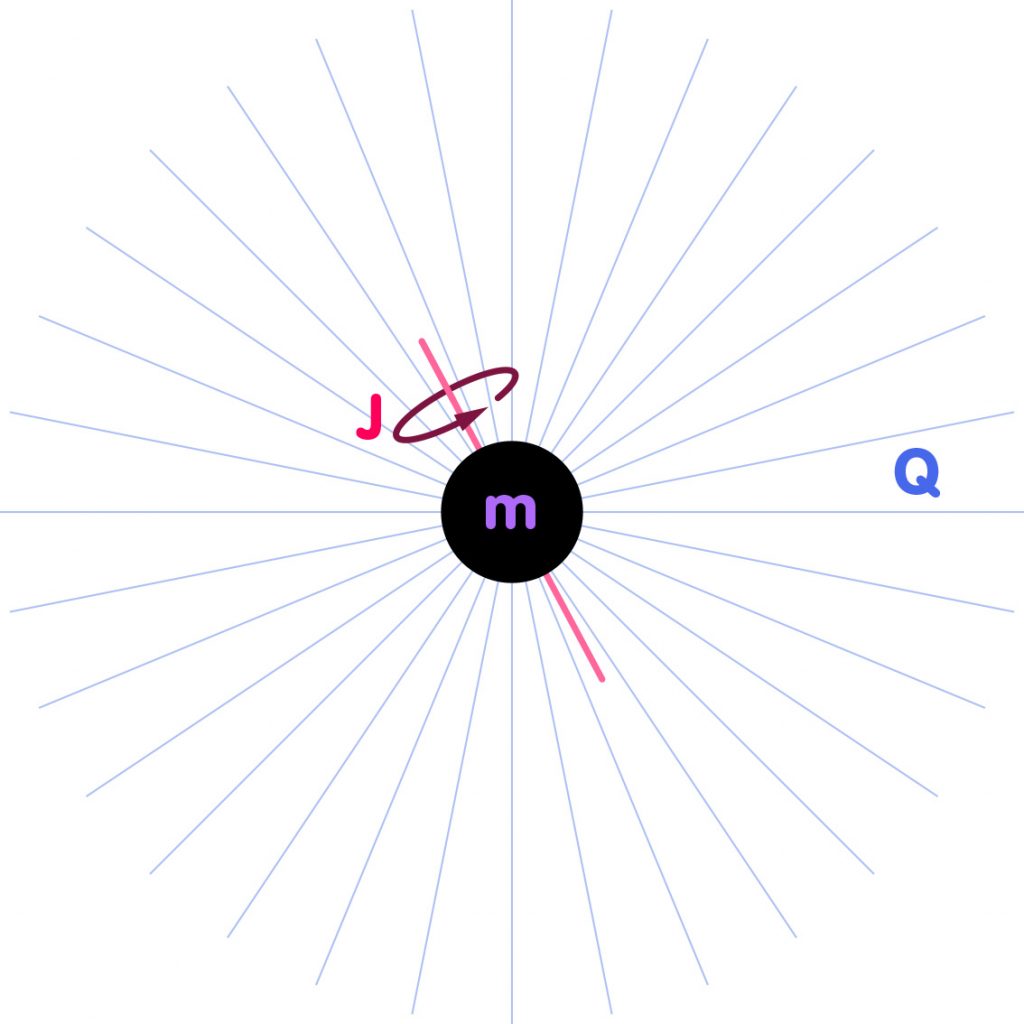
Eine erweiterte Version der Eindeutigkeitstheoreme zeigt, dass dies tatsächlich alle stationären Schwarzen Löcher mit elektrischer Ladung sind – und da haben wir sie, die einzigen drei charakteristischen Eigenschaften Schwarzer Löcher: Masse, Drehimpuls und elektrische Ladung.
Zurück zur Astrophysik
Strenggenommen beziehen sich die Eindeutigkeitstheoreme auf einsame Schwarze Löcher, denen unendlich viel Zeit zur Verfügung stand, um in einen stationären, zeitlich unveränderlichen Zustand überzugehen. Aber zumindest näherungsweise sollten sie auch für realistischere Situationen gelten, die sich von dieser Idealsituation in zweierlei Hinsicht unterscheiden: Zum einen ist das betreffende Schwarze Loch kein isoliertes Objekt in einem ansonsten leeren Universum, sondern lediglich ein isoliertes Objekt in einer anderweitig leeren Raumregion. Zweitens hatte es nicht unendlich viel Zeit, in einen stationären Zustand überzugehen, aber immerhin einen langen Zeitraum verglichen mit der Zeit, die es benötigt, um „seine Haare zu verlieren“, also etwaige an den Kollaps erinnernde Eigenschaften in Form von Gravitationswellen abzustrahlen.
Das sind gute Neuigkeiten für Astrophysiker: Auch realistische Schwarze Löcher dürften durch die wohlbekannte Kerr-Lösung beschrieben werden, vorausgesetzt, sie hatten genügend Zeit, um Gravitationswellen abzustrahlen. Und den Forschern, die Gravitationswellendetektoren betreiben, versprechen die Prozesse, während derer Schwarze Löcher „ihre Haare verlieren“ attraktive Gravitationswellenquellen.
Weitere Informationen
Die relativistischen Grundkonzepte, die diesem Vertiefungsthema zugrunde liegen, werden in Einstein für Einsteiger erklärt, insbesondere im Abschnitt Schwarze Löcher & Co.
Verwandte Vertiefungsthemen auf Einstein-Online finden sich in der Kategorie Schwarze Löcher.
Eine Einführung in die Welt der Eindeutigkeitssätze auf höherem fachlichen Niveau bietet der E-Print „Stationary Black Holes“, gr-qc/0502041.
Kolophon
ist Professor für Gravitationsphysik an der Universität Wien. Sein Forschungsinteresse gilt einer Vielfalt von mathematischen Themen, die im Zusammenhang mit den Einstein-Gleichungen stehen.
Zitierung
Zu zitieren als:
Piotr Chrusciel, “Wie viele verschiedene Arten von Schwarzen Löchern gibt es?” in: Einstein Online Band 04 (2010), 02-1104