Equilibrium and Change: The physics behind Big Bang Nucleosynthesis
The physics behind Big Bang Nucleosynthesis, the period shortly after the big bang that saw the first production of light elements such as helium and lithium
An article by Achim Weiss
Studies of Big Bang Nucleosynthesis – the formation of atomic nuclei like those of helium, deuterium or lithium in the early universe – have led to some of the most impressive predictions of the big bang models. A brief overview can be found in the spotlight text Big Bang Nucleosynthesis: Cooking up the first light elements – here, we take a closer look at the physics behind the predictions.
Shifting equilibria
Leaving the uncertain earliest phases of the big bang aside, the early universe was filled with a hot plasma consisting of radiation and elementary particles. The various ingredients of this mixture were in thermodynamic equilibrium.
By definition, in thermodynamic equilibrium the energy is distributed evenly among all components of a system. For a simple gas, this would mean that, on average, all of the myriads of particles flying around have the same kinetic energy. For systems like the matter content of the early universe, there is an additional aspect: The particles are constantly involved in reactions in which one kind of particle is converted into another, or several other particles.
For such a system, thermodynamic equilibrium at a certain temperature corresponds to definite values for the relative abundances of the different particle species – how many particles of species A there should be, on average, for each particle of another species B. The relative abundances depend on the temperature, and as the temperature changes, so does the particle mix in the early universe.
From fog to elementary particles
Such changing equilibria are a more general phenomenon, and examples can be found much closer to home than in cosmology. On a cool autumn evening, chances are that the mixture of water vapor and fog droplets in the outside air is in (temperature- and pressure-dependent) equilibrium. Both the gaseous and fluid forms of water are present, and are constantly being transformed into each other: At any point in time, there will be some droplets evaporating and, in turn, some vapor will condense into droplets:
The equilibrium that is reached – in a given region of space, how much water in droplets as opposed to vapour? – depends on the temperature. If we now imagine that the air temperature is dropping as evening turns to night, the rate of condensation increases. As a result, there will now be more water in the form of droplets, corresponding to denser fog than before. If temperature is kept constant, so will the thickness of the fog. If, on the other hand, the temperature starts rising again in the morning, evaporation becomes much more common than condensation, and the air will clear as more and more droplets are converted to water vapor. The process only stops once all droplets have vanished.
In equilibrium, the ratio of vapor to fog droplets can be described by statistical formulae which contain a certain “potential” (approximately the energy needed to convert vapor into condensed water – the binding energy) as well as the controlling parameter, namely the temperature (or, equivalently, the thermal energy).
Since matter in the universe started out in equilibrium, these same statistical formulae can be applied, telling us how the initial mix of particles changed as new particles were formed. Again, the ratio of particle binding energy to thermal energy is an important factor in determining the fraction each particle species contributed to the total number of particles.
A cosmos in equilibrium
Let’s trace the development starting at about a hundredth of a second and ending at three minutes cosmic time. At the beginning of this time period, the universe was filled with a plasma consisting of matter well-known to physics: protons and neutrons in about equal proportions constituting what physicists call baryonic matter, as well as electrons, their anti-particles (positrons), neutrinos, and photons. On average, each of these myriads of particles had the same energy. Just as in the case of fog, droplets and water vapor, this equilibrium was by no means static: constantly, there were particle reactions in which particles decayed, or combined to form new particles. But on average, the number of particles of each species, as well as the energy they contributed to the total energy content of the universe, remained the same.
In this particular epoch, the most influential mediating forces responsible for the particle reactions were electromagnetic interactions and interactions via the so-called weak nuclear force (which is responsible for certain forms of radioactive decay). There were many competing types of reactions going on. For instance, via the weak nuclear force, protons were continually being converted into neutrons, and vice versa. The reactions in question are illustrated below. Here, a proton and an electron combine to give a neutron and what is called an electron-neutrino (a nearly massless particle that is electrically neutral):

In turn, a neutron can combine with a positron to give a proton and the electron-neutrino’s antiparticle:

If we take all these reactions into account, the statistical formula that govern thermodynamic equilibrium give us a ready answer for the particle content of the very early universe, namely that there were about as many protons as neutrons.
Too fast for adjustment: The race between equilibrium physics and change
There is, however, a complication. If external conditions change, it will take a while for a system to settle in the new equilibrium state. In the early universe, this fact became increasingly important.
The time it takes for a system to adjust depends on how closely its particles are in contact. After all, to reach thermodynamic equilibrium, energy must be distributed evenly throughout the system, so that, on average, each particle has the same energy. If each particle is in contact with others a million times a second, any redistribution of energy will come about very quickly. If, on the other hand, the particles interact only rarely, it will take a long time to reach thermal equilibrium.
Reaction rates depend on particle energy and particle density, among other factors. As the external conditions change, the reaction rates will change as well. In extreme cases, particle interactions of some type can become so rare that their contribution becomes completely insignificant. This is called “freezing out” – from this point on, the relevant particle abundances and the energy distribution remain unchanged, even if they are markedly different from the equilibrium values.
In this way, the consequences of external change are a matter of time scales: If we alter external conditions very slowly compared to the time it takes the system to adjust, then, throughout the change, the system will always be in some kind of equilibrium state. If, on the other hand, we change the external conditions quickly, then throughout the change, the system will be in some non-equilibrium state, not quite having caught up with the altered conditions.
In the early universe, the external conditions were constantly changing as the universe expanded and cooled down. The particle mixture at a given point in time depended on the race between reactions establishing the temperature-dependent equilibrium and the change of this very temperature due to cosmic expansion.
Freezing out the weak interactions
As far as our protons and neutrons are concerned, until about a tenth of a second cosmic time, the weak interactions took place fast enough to maintain equilibrium. Afterwards however, when the temperature had fallen below a hundred billion Kelvin (corresponding to an energy of 10 MeV per particle), things began to change: At this temperature, the reaction rates for weak interactions between neutrinos and the electromagnetic radiation field are so small that the two kinds of matter effectively “decouple” and cease to interact at all. In addition, most of the electrons and positrons annihilated, while the electromagnetic radiation had cooled down too far to produce new electron-positron pairs. The result was a heating-up of the radiation field (but not of the neutrinos, which had decoupled). A slight imbalance in the number of electrons and positrons led to a small surplus of electrons being left behind – those are the electrons we still find in the cosmos today.
While, at the beginning of this new epoch, neutrons and protons were still present in ratios of 1 neutron for every 6 protons, which is close to the equilibrium value at this particular temperature, equilibrium could not be maintained. The only way to reach equilibrium would have been via weak interactions like the one sketched above, and at this point in time, with so much fewer electrons and with hardly any positrons left, such reactions took place only very rarely. The expansion changed the cosmos much faster than these reactions could keep up equilibrium – just such a race between cosmic expansion and specific reaction rates as was mentioned above: the weak reactions “froze out”. As a result, almost the only weak reaction that still took place at a significant rate was the decay of neutrons into the slightly lighter protons, which is in fact independent of temperature. This radioactive decay has a half-life of about 889 seconds – in any ensemble of free neutrons, if you wait for this time, then at the end about half of the neutrons will have decayed into protons.
Cooking up light atomic nuclei
This is were the expansion rate of the universe became crucial indeed. If, at this time in its evolution, the universe had expanded somewhat faster than it actually did, then all neutrons would have been gone within an hour, leaving behind nothing but protons. Fortunately, however, the universe expanded (and cooled) slowly enough to give another type of reaction time enough to occur: reactions in which neutron and protons combined to form light atomic nuclei. The universe entered the phase called Big Bang Nucleosynthesis (often abbreviated to BBN).
How many atomic nuclei of which type were formed during this phase? This is, again, a question of reaction rates, equilibrium and cosmic expansion. And again, there are many different reactions to consider. For instance, a proton and a neutron can combine to form the nucleus of deuterium (a heavier variety of hydrogen), and by addition of either a proton or a neutron, we can obtain nuclei of helium-3 (a light variety of helium) or tritium (an even heavier variety of hydrogen), respectively.
At the beginning of Big Bang Nucleosynthesis, at a cosmic time of about 1 second, the situation was quite simple: The nuclear reactions occured fast enough to achieve equilibrium, which strongly favours the very light elements like hydrogen and helium and their isotopes deuterium (d), tritium (t), and helium-3. At this time, the temperature of the radiation-matter-plasma was around ten billion Kelvin, corresponding to an average 1 MeV of energy per particle. Nuclear physics and all the reaction rates necessary for the equilibrium calculations are very well known, as energies like this are easily achievable in laboratory experiments with nuclei.
Until about 1 minute cosmic time, nothing much happened: The ratio of neutrons to protons remained constant at around 1:7 (one neutron for every seven protons – the time had not nearly been long enough for a significant fraction of the neutrons to decay radioactively). Note that, if we could have halted the universe’s expansion at this time, long enough for the weak interactions to lead to an equilibrium state, then the ratio would have dropped to one neutron for every 74 protons! Instead, the expansion continued, and within the next two to three minutes, the temperature sank from 3 to about 1 billion Kelvin (from 0.3 to 0.1 MeV energy per particle).
This expansion was slow enough for a rather fast type of reaction to become significant: The capture of neutrons by protons and light nuclei. In this way, ever heavier nuclei can be built up, following the sequences sketched here:
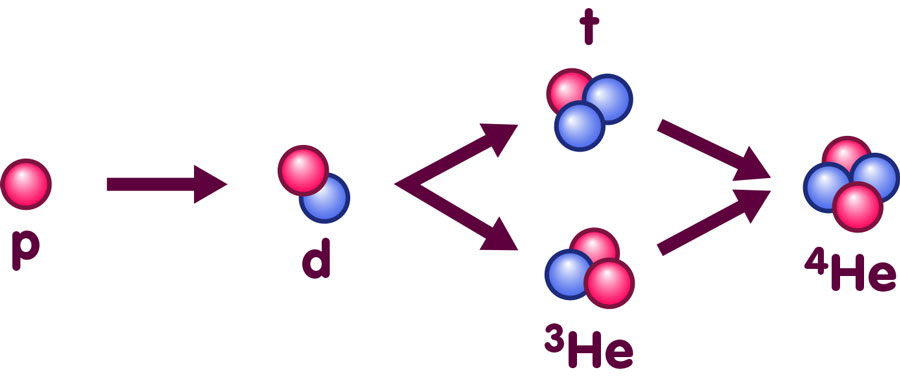
The isotope helium-4, or 4He, is in fact the most tightly bound nucleus of all (for more information about nuclear binding, see the spotlight text Is the whole the sum of its parts?). As such, it is a greatly preferred state in a lower-temperature equilibrium situation, and if we had halted cosmic expansion at this point and simply waited, we would have gotten a universe filled almost exclusively with helium-4 nuclei. Even the protons would have combined, some of them changing into neutrons in the process, to form helium-4 nuclei consisting of two neutrons and two protons apiece.
But in fact, cosmic expansion was comparatively fast, and the processes that involve protons changing into neutrons are rather slow. Once more, matter failed to reach an equilibrium state, and its final composition was the result of a race between expansion and nuclear reactions.
It is easy to make an estimation of the result of that race. Considering the relevant time scales for the expansion of our universe and for nuclear reactions, it turns out that hardly any protons will have had time to join existing nuclei and transform into neutrons. On the other hand, reactions in which existing protons and neutrons join to form nuclei were fast enough to ensure that all helium-4 nuclei that can form in this way would indeed have formed. Finally, as mentioned above, we know that, at the beginning of nucleosynthesis, the ratio of neutrons to protons was one to seven – seven protons for each neutron.
With this information, the estimate is straightforward: Consider 16 nucleons, of which 2 are neutrons and 14 are protons (this is precisely the near-equilibrium ratio of 1:7). Out of these one can build only one helium-4 nucleus (as each such nucleus consists of two neutrons and two protons). It has an atomic mass of 4. What remains are 12 protons or, put differently, 12 nuclei of hydrogen atoms, each of which has an atomic mass of 1. The mass ratio of helium-4 to hydrogen is therefore 4/12, in other words: by mass, 75% of matter in our universe is hydrogen and 25% is helium-4. This is a rather simple and solid prediction based on no more than equilibrium physics in a well-known temperature regime.
If we look more closely, this picture is somewhat too simple. More accurate calculations of the relative abundances of atomic nuclei in the early universe are based on a whole network of nuclear reactions, the most important of which are sketched in the following figure:
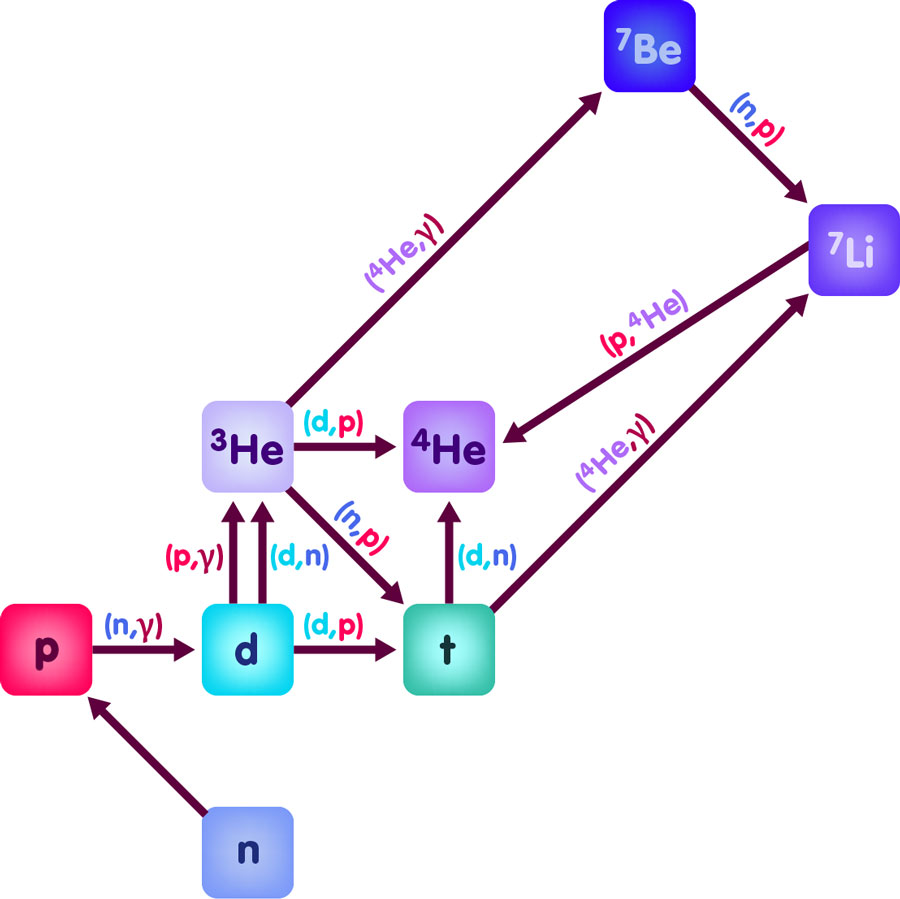
In this diagram, the distance of a nucleus from the bottom line is proportional to the number of protons it contains, while its distance from the left border corresponds to its number of neutrons. The different reactions are represented by arrows pointing from one kind of nucleus to another. The arrows are labelled, giving some details about the reaction in question. For instance, the arrow pointing from deuterium d to tritium t has a label (d,p), meaning that, in order to transform a deuterium nucleus d to a tritium nucleus, we need to add a further deuterium nucleus d, and the result will be tritium and an additional proton p. Analogously, to get from deuterium to helium-3, we need to add a proton p, and the result will be not only helium-3, but also a photon, which is usually denoted by the greek letter gamma. Hence, the arrow pointing from deuterium to helium-3 is labelled with (p,γ). Alternatively, another d can be added, with an extra neutron being set free in the reaction.
The diagram shows 12 nuclear reactions. In full calculations, more isotopes of lithium and even heavier elements are included, and some fourty possible reactions are taken into account – all this before the backdrop of an expanding universe in which most of the energy has the form of electromagnetic radiation. Most of the parameters entering the calculations – reaction rates, the initial ratio of protons to neutrons – are well-known, except one: the overall density of baryonic matter, in other words: how many neutrons and protons are there in a given region of the early cosmos? This density parameter directly influences the outcome: if the density is higher, the nuclear reactions occur more frequently, the production of helium-4 via the intermediate stages of deuterium and helium-3 occurs more quickly, the free neutrons have less time to decay radioactively into protons. Overall, more helium-4 is produced and, in turn, there are less nuclei of deuterium and helium-3. Conversely, if we can measure the abundances of these light elements in the early universe, and find that it corresponds to the predictions of Big Bang Nucleosynthesis for a certain proton/neutron density, we have in fact derived the density of baryons (protons plus neutrons) in the universe!
The results of such calculations for one specific value of the baryon density (one baryon for every 3 billion photons) are shown in the following figure:
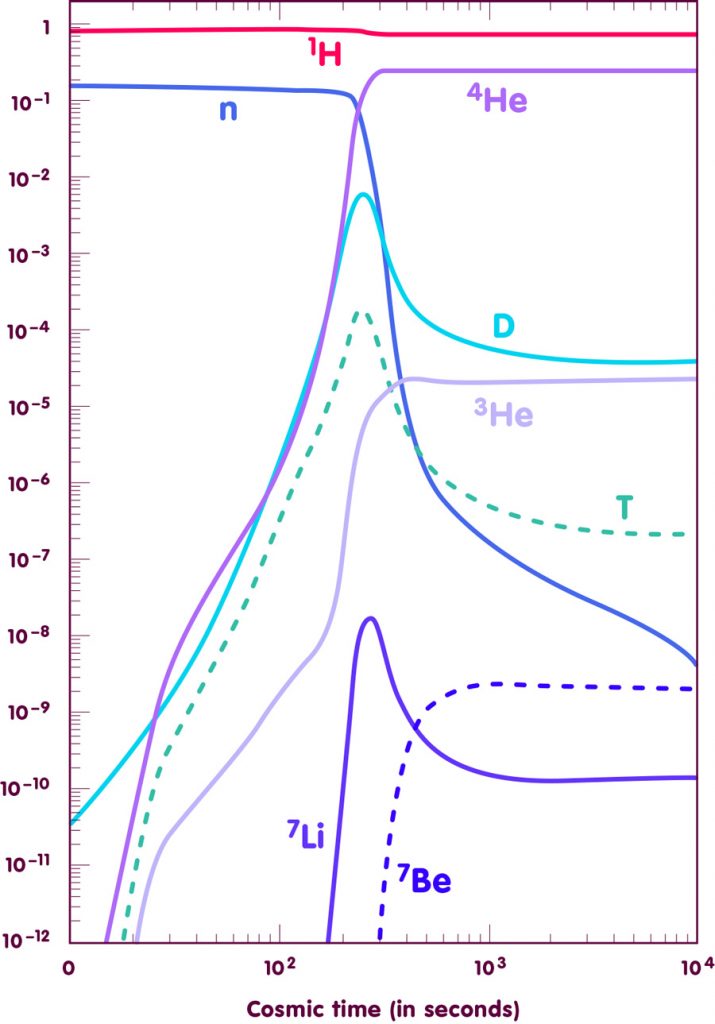
[Adapted from an image by E. Vangioni, Institut d’Astrophysique de Paris]
Big Bang Nucleosynthesis leads to some of the most successful predictions derived from the big bang models: The physics of the expanding universe at cosmic times of 1 to 3 minutes is well established, and rather simple. As a result, the predictions about the abundances of the light elements in the early universe are clear and solid. Observations have shown that they are also highly accurate – clear indication that the big bang models paint an accurate picture of the early universe. In addition, as was mentioned above, the observations allow astrophysicists to determine an important cosmological parameter: the baryon density of the universe. More details about the astronomical observations and their comparison with the theoretical predictions can be found in the spotlight text Elements of the past.
Further Information
For the relativistic ideas behind this spotlight topic, check out Elementary Einstein, especially the chapter Cosmology.
An overview of Big Bang Nucleosynthesis can be found in the spotlight text Big Bang Nucleosynthesis: Cooking up the first light elements; information about observations of element abundances in Elements of the past. Other related spotlights on relativity can be found in the section Cosmology.
Colophon
Achim Weiss is a scientist at the Max Planck Institute for Astrophysics in Garching near Munich, in Germany. His main area of research is stellar physics.
Citation
Cite this article as:
Achim Weiss, “Equilibrium and Change: The physics behind Big Bang Nucleosynthesis” in: Einstein Online Band 02 (2006), 02-1018