Gravity: from weightlessness to curvature

So what is gravity in Einstein’s theory? The answer: in part, an illusion; in part, an aspect of geometry.

An article by Markus Pössel

What is gravity? Einstein’s general theory of relativity has an unusual answer to that question which will be explored in this spotlight text. In part, gravity is an illusion. In part, it is associated with a quantity called “curvature”. Overall, gravity is intimately connected with the geometry of space and time.

The elusiveness of gravity

One central feature of gravity is that it makes no distinctions. At least in a vacuum (where there’s no air resistance), objects you place at the same location fall with the same acceleration – the mouse or the elephant, the feather or the cannonball.

This seemingly harmless property has far-reaching consequences. Imagine a scientist in a small elevator; more precisely, in a small, windowless compartment that looks like an elevator cabin) That scientist has great difficulty to tell whether she is in free space, far from all sources of gravity, or in free fall in a gravitational field. In both situation, she would float, weightlessly, in the elevator, as would all objects around her.

Most readers will have seen footage showing situations like this, involving, for instance, astronauts aboard the international space station ISS. Those astronauts haven’t escaped the earth’s gravity – they’re experiencing a very special kind of free fall, a free-falling orbit around the earth. As an example, the following picture shows the astronaut-scientist C. Michael Foale aboard the ISS, together with two floating grapefruits:

Astronaut C. Michael Foale on the ISS
© NASA

Under these circumstances, the physical laws which govern whatever is happening in the free-falling elevator, or in any other small room which is in free fall, are the same as those of special relativity, the laws that hold for a freely drifting observer far away from all sources of gravity. (This statement is known as the equivalence principle, and it is explored further in the spotlight text The elevator, the rocket, and gravity: the equivalence principle.)

Does that mean gravity is merely an illusion? For the usual, constant gravitational force we know from everyday life on earth, that appears to be the case. This is readily apparent when we look at a slightly different situation pictured in the following illustration:

Different observers in space

We, the crew of the spaceship shown on the right, are floating freely in space, far away from all major sources of gravity. Now imagine that there is another observer in a spaceship, shown on the left: The rocket engine of that observer’s spaceship is firing and produces an acceleration of 9.8 metres (32 feet) per square second. This accelerated observer feels as heavy as we would feel on earth, since the gravitational acceleration with which an object on earth falls to the ground has that exact same value.

Our accelerated observer has a clear notion of “up” and “down” – when he looks up, he sees all freely drifting observers and their space stations “fall downwards”, in the direction of his own spaceship’s floor. “Upwards” is the direction in which his spaceship is accelerating. But there is no gravity in this situation. All the observers in freely drifting spaceships (rocket engines shut off) are in agreement: The fact that the accelerated observer sees objects “fall” is merely an artefact, brought about by his spaceship’s acceleration – it vanishes as soon as you leave the accelerated reference frame and change to a free-falling one.

Is the same true for gravity here on earth? Is it an artefact of the unnatural, accelerated reference frame from which we observe the world – and does it vanish as soon as we change to a freely falling reference frame?

The remains of gravity

In fact, earth’s gravity does not vanish completely even in a free-falling reference frame (it cannot be “transformed away”, as physicists would say).

To see why, have a look at this freely falling elevator of gigantic size, with two freely floating gigantic spheres inside. The following animation shows the elevator falling towards the earth, following our planet’s gravitational pull:

Under these circumstances, it becomes important to note that bodies falling towards the earth do not all move in the same direction (“down”) – they move towards one and the same point in space, namely towards the earth’s center of gravity. That is why even an observer inside the falling elevator will see some residual of the earth’s gravitational force at work: She doesn’t notice the downward pull – after all, she is falling alongside all other objects within the elevator. But she does notice the fact that the distance between the two spheres is shrinking steadily, little by little, over time.

The reason for the shrinking distance? The gravitational force pulls the left sphere into a slightly different direction than the right – simply because both spheres get pulled towards the earth’s center. It is this difference in directions that’s responsible for the two sphere’s decreasing distance, a force difference that physicists call a tidal force. (Why tidal? Just such a difference in the moon’s gravitational attraction on the earth and on the earth’s oceans is responsible for the tides.)

Tidal effects become even more drastic when an observer considers falling bodies on opposite sides of the earth. Sure, the falling bodies at his side still float as if there were no gravity at all. But bodies on the opposite side of the earth accelerate towards our observer with twice the usual gravitational acceleration!

All this serves to show the difference between an observer on earth and an accelerated observer in gravity-free space: The accelerated observer need simply change his frame of reference – for instance, switch off his rocket engine. Immediately, what he thought to be a constant “gravitational force” vanishes. Earth’s gravity cannot be made to vanish simply by letting go and falling freely. Sure, if we restrict ourselves to a limited observation period in a small, freely falling cabin, we won’t notice the difference to floating freely in gravity-free space. But the larger our elevator, the longer our period of observation, the better are our chances of noticing residual gravity – tidal forces.

Planes and curved surfaces

Oddly enough, this elusiveness of gravity has an analogue in pure mathematics, more specifically: in the theory of distorted or curved surfaces.

The plane is the simplest of two-dimensional surfaces – like a sheet of paper, but infinitely extended in all directions. In the plane, as on paper, the shortest connection between two points is a straight line. Straight lines can be used to construct more complicated geometric objects, such as triangles:

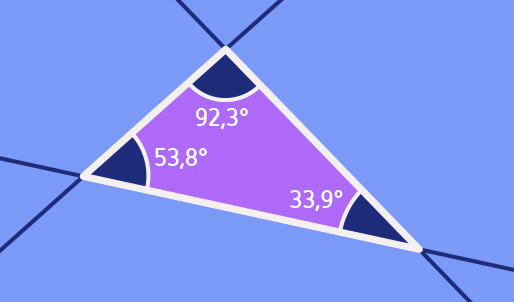
Plane with triangle whose angles add up to 180 degrees

The properties of geometric objects obey a set of rigid laws. For instance, the sum of all the angles of a given triangle will always be 180 degrees, and for triangles with a right angle, Pythagoras’ theorem holds true.

A perfect plane is only the simplest example of a surface. From everyday experience, we know of distorted, curved surfaces – say, the surface of a sphere, that of a saddle, or the undulating surface left in the sand when the flood has receeded. On those more general surfaces, the laws of geometry are somewhat different. As an example, take a surface that is, in itself, rather simple: a sphere. There are no straight lines on a sphere – all one can construct are straightest lines. Mathematicians call such lines-that-are-as-straight-as-possible geodesics. In the case of the sphere, they are also called great circles, as they are the largest circles that one can possibly construct on that surface, the best-known example being the equator. The shortest connection between two points on a sphere will always correspond to some part of a suitably chosen great circle.

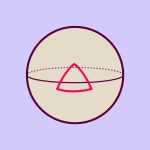
The following figure shows a sphere as well as, in green, a triangle formed by three intersecting geodesics:

Sphere with geodesic triangle

The two angles of the triangle that lie along the equator (red line) are both right angles – they alone add up to 180 degrees. The total sum, which includes the angle that is at the North pole, is evidently larger than 180 degrees. The surplus can, in fact, be used to define a measure for the sphere’s curvature (and thus for the difference between its geometry and that of a plane).

The elusiveness of curvature

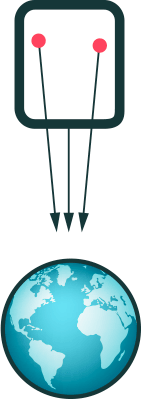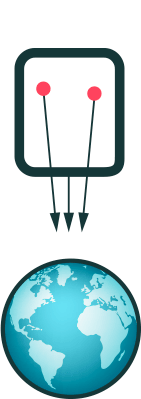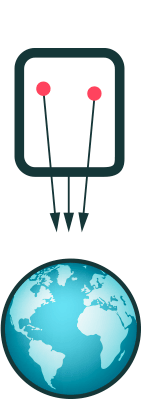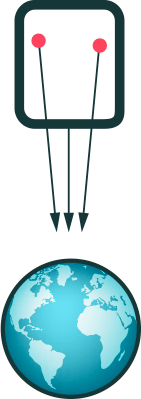
But in spite of the differences in geometry, the following still holds: If you look at a tiny region of the sphere’s surface, you’ll be hard-pressed to find a difference between it and the corresponding region on a plane. In fact, that’s what we do every day: We draw city maps, which show a comparatively small part of the earth’s surface, just as if the city had the same geometry as that flat sheet of paper we’re drawing on:

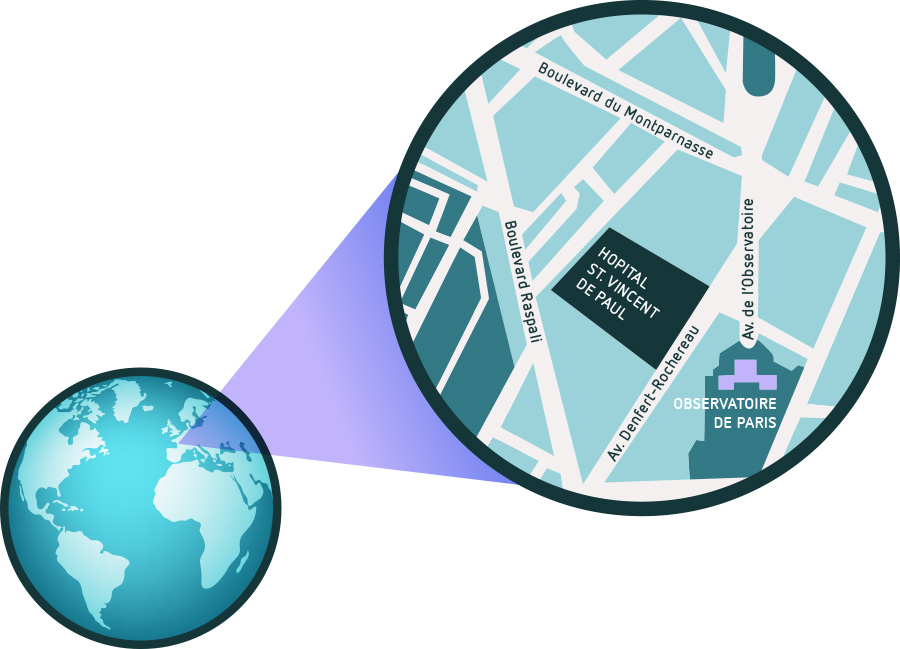
This works quite well, although, in reality, the city region is part not of a gigantic plane, but of the surface of a gigantic sphere, the earth. Only when you look at larger regions will you notice that the surface is, in fact, curved; the larger the region, the more distinct the signs of curvature.

The same is true for any curved surface: a tiny region of such a surface looks almost exactly the same as part of a plane. This indistinguishability is exactly analogous to the elusiveness of gravity that has been described above: For a very small spacetime region, say, the elevator of a free-falling observer, gravity is absent. Over a brief observation period, the interior of the elevator looks as if it were part of the spacetime of special relativity, where there is no gravity at all. Only in a larger spacetime region, the differences become measurable. Residual gravity, tidal forces come into play. This is completely analogous to geometric curvature: The larger a region of our curved surface, the larger the deviations from flat geometry, for instance from the law stating that angles of a triangle always sum up to 180 degrees.

Einstein took this analogy seriously, and he found that he could make it much more precise.

The geometry of gravity

In the “flat” spacetime of special relativity, where gravity is absent, the laws of mechanics take on an especially simple form: As long as no external force is acting on an object, it will move on a straight line through spacetime: at a constant velocity along a straight path.

Now we add gravity to the situation, for instance by placing a massive sphere somewhere in space. In Newton’s theory of gravity, this sphere will exert a force on all other masses around it. If we place a test particle in the vicinity, we see that its movement is deflected away from the usual straight spacetime line – its path would be curved towards the sphere and it would become accelerated as it feels the sphere’s attraction.

In Einstein’s geometric theory of gravity, the situation is described in a completely different way: A mass that we place in an region of space will lead to a distortion of spacetime. Empty spacetime is flat – it looks exactly like the spacetime of special relativity. Spacetime in the presence of masses is curved. In curved spacetime, there are no straight lines – just as there are no straight lines on the surface of a sphere. The closest we can get to the notion of a straight line is a geodesic, a spacetime curve that is as straight as possible. Test particles in the vicinity of the massive sphere follow these geodesics. Gravity does not reflect them from their straight lines – it re-defines what it means to move on a straightest possible line.

Einstein’s universe performs an ever-ongoing cosmic dance, with matter and spacetime interacting: A given configuration of matter distorts spacetime geometry. This distorted geometry makes matter move in certain ways. The movement changes the matter configuration as the sources of gravity change their locations. With the matter configuration changed, spacetime geometry changes as well. Now that spacetime geometry is a bit different, it also acts on matter in a different way, matter moves, geometry changes, and so on in an endless dance.

So what is gravity, in Einstein’s universe? Generally speaking, any distortion of spacetime geometry. More precisely, there are two sides to gravity: In part, gravity is an observer artefact: it can be made to vanish by going into free fall. Most of the gravity that we experience here on earth when we see objects falling to the ground is of this type, which we might call “relative gravity”. The remainder of gravity, “intrinsic gravity”, if you will, manifests itself in tidal forces, and is associated with a specific property of geometry: The curvature of spacetime.

Further Information