Varying Newton’s constant: A personal history of scalar-tensor theories

Information about a modification of Einstein’s theory of general relativity in which the gravitational constant is not a constant.

An article by Carl H. Brans

The paradoxical phrase, “Varying…constant” in the title was first used by me in my Princeton PhD thesis of 1961. There I developed a formalism making explicit modifications of Einstein’s theory introducing a scalar field variable to determine the Newtonian universal gravitational “constant,” G. These ideas were first suggested to me by R. H. Dicke motivated by ideas of Mach, Dirac, et al. He and I published the first paper on our version of this subject in 1961, although P. Jordan and his colleagues had earlier and independently developed their own version. Consequently, these theories ought properly be called “Jordan- Brans-Dicke,” (JBD), although unfortunately many papers disregard Jordan’s groundbreaking work and refer to it simply as “Brans-Dicke”. A more neutral term is “scalar-tensor theories” (ST theories).

The constant G made its first appearance in classical gravity, centuries before Einstein. In 1687, Newton published his theory of universal gravitation which unified astronomical phenomena, such as planets orbiting the sun, to our everyday experiences with weight, or gravity, on the earth. Starting with Kepler’s analysis of planetary motion, Newton used his laws of mechanics to suggest that all masses attract each other with a force proportional to the product of their masses and inversely proportional to their separation distance squared. For our purposes, the key word here is “proportional”. The statement of proportionality was the best Newton could do with the data at hand. It was only after the British scientist Henry Cavendish performed a very difficult experiment in 1798, actually measuring the extremely tiny force between known masses in the lab a known distance apart, that the first estimate of the constant of proportionality, namely G, was obtained. Today, we know that G ≈ 6.7 × 10⁻¹¹ m³/kgs² in laboratory and solar system environments. But, is G really constant, or is it a function of the matter distribution in the universe? That is the question which ultimately led to a class of theories, the so-called scalar-tensor theories, that we will survey in this article.

These theories presented the first possibly viable alternative to the standard general relativistic theory of gravity proposed by Einstein. The existence and wide spread promulgation of such theories, primarily by R. H. Dicke, beginning in the 1960’s provided experimentalists with a renewed motivation to empirically explore the validity of Einstein’s theory of gravitation. Serendipitously, this was also the era in which NASA began directly exploring the solar system. The motivation to compare Einstein’s theory against an alternative one resulted in a proliferation of solar system experiments. It turns out that, within experimental error, Einstein’s theory fared better than scalar-tensor theories, or at least restricted the theoretically undetermined constant ω contained in them to a range essentially making the ST theories indistinguishable from Einstein’s in the solar system environment. Consequently, ST theories fell into disfavor until later developments in the 1970’s and 1980’s in cosmology and superstring theory led to renewed interest in them. These are the topics we will survey in the following.

Inertia and gravity

During the development of general relativity, Einstein was strongly influenced by the surprising parallels between what physicists call inertial forces and Newtonian gravitational forces. Unless you get dizzy easily, you can experience one particular example of an inertial force for yourself. Stand up, let your arms hang by your side, and start turning a pirouette around your body’s vertical axis. You will experience an inertial force known as “centrifugal force” pulling your arms outwards.

There is one particularly interesting point of similarity between inertial forces and the gravitational force. An inertial force such as this centrifugal force is proportional to the mass of the object being pulled. The same is true for gravity, the gravitational force that pulls an object towards Earth. This force (also called “weight”) is also proportional to the mass of the object it acts on.

Why this similarity? Could it be that, as the Austrian physicist and philosopher Ernst Mach surmised, the similarity points to a deeper connection? Could inertial forces themselves be a novel type of gravitational influence exerted by the distant fixed stars – could there be a causal relationship between all those far-away masses in the rest of the universe rotating around you and the force acting on your arms?

In fact, as early as 1912 Einstein published a paper mentioning the influence of Mach’s work on his thoughts about gravity. This was some three years before Einstein published his own theory of gravity, general relativity, which he believed conformed to Mach’s ideas about inertia and gravity. In the 1920’s, Einstein claimed that general relativity could even be used to show explicitly how the inertial forces depended on the overall mass distribution of the universe. The model universe Einstein used to demonstrate this claim was finite in size, its space the three-dimensional analogue of the surface of a sphere with radius R, and it contained matter with a total mass M. Interestingly enough, by Einstein’s argument, the relation between inertial forces and the overall mass distribution held only if there was a special relationship between M, R and Newton’s gravitational constant G, namely

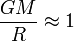
or

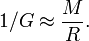
Here we have chosen units so that both time and length are measured in seconds (one second of length, also known as one light second, is the distance travelled by light in one second).

Ultimately, Einstein was on the wrong track in ascribing inertial forces to the influence of distant masses alone. This is not to say the relationship between inertial forces and gravity is not important. But the essential question is not whether inertial forces are caused by distant masses, but another property of which Einstein made extensive use in developing his theory: Inertial forces can be “transformed away”, as physicists say. Specifically, they can be made to vanish by simply making the transition from one observer to another (in our example, by making the transition from a rotating observer to a non-rotating one). The same is true for gravity, which can be made to vanish, at least locally and approximately, if you just let yourself fall freely.

Cosmic coincidence?

Developments in cosmology soon left Einstein’s unchanging, finite universe behind. From the early 1930’s onwards, following observations by the American astronomers Edwin Hubble and Milton Humason, it became clear that we live in an ever-expanding and possibly infinite universe which, a finite time ago, emerged from an extremely hot and dense initial state known as the big bang. Yet even in such a universe, the equation relating G and the size and mass of the universe seemed to hold, although with a somewhat different meaning of the terms R and M: In a universe that came into being a finite number of years ago, astronomers cannot observe objects more distant than a maximal distance R. Simply speaking, this is because light from more distant regions of the universe has not had sufficient time to reach us. Denote the mass of all the objects you can see up to that maximal distance as M. As observational cosmology developed, it appeared that the equation

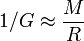
is indeed at least approximately valid for our universe – at least given the data that was available from the 1930’s to the 1950’s.
When you think about it, the fact that there is a relation like this is either a truly amazing coincidence or it may indicate that Newton’s gravitational constant, G, depends on the mass distribution of the universe!

First, why would this be a “truly amazing” coincidence? In an expanding universe, the radius R of the observable universe increases with time – as more time passes, light from ever more distant regions can reach us. The mass M of matter in the observable part of the universe increases as well, but in a way that means the quantity M/R will also change with time. If G is constant, and M/R varies over time, then the equation 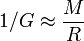will only hold, even approximately, during a brief period of time, which is very short compared with the long history of the cosmos. The amazing coincidence is that this should just happen to be the period of time in which humans observe the sky with powerful telescopes, and discover mathematical models of an expanding universe.

This was just one of a number of apparent numerical coincidences studied by the English physicist Paul Dirac in the late 1930’s, in the context of what became known as his “Large Numbers Hypothesis”. Dirac suspected that, in fact, the coincidences he had studied were anything but. In the cosmology he developed, our equation denotes a systematic relationship between G,M and R.

From a modern point of view, Dirac’s cosmology is little more than a historical footnote. But in the context of scalar-tensor theories, it did introduce a fruitful new idea: If G,M and R are related, and if M/R changes with time, then G cannot be a constant, either.

What if G is not a constant?

The relation between M, G and R given in the above equation is, in fact, reminiscent of another kind of physical law. Let us leave gravity behind for a moment and consider an electric charge. One way of expressing the way it influences other charges in its neighborhood is by giving what is called its electric potential, V , measured in the familiar unit, volt. At every point in space, V has one particular value. In the language of physics, this makes V a “field”. Furthermore, the value is a simple number (as opposed to, say, specifying a force, for which you would need more than a single number – you would have to define both the force’s strength and its direction). Physicists call such a field a “scalar field.”

Most readers will be familiar with one particular application of the electric potential. The “strength” of a battery is measured by its “voltage,” which is the difference of V between the two poles of the battery. The interesting thing is that the potential near an electrically charged particle is given by

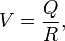
where Q is the magnitude of the particle’s electric charge, and R is the distance between the particle and the point for which we want to find the potential. This equation looks very similar to the one we have found, above, for 1/G – in both cases, there is on the right-hand side a charge (either the electrical charge or a mass, a “gravitational charge”) divided by a length. This suggests that 1/G might itself be a scalar field, whose current value depends on the mass and other properties of the observable universe at a given time.

Note that we are not saying that 1/G should be identified with the electric potential, and depend explicitly on electric charge. We are only pointing out the similarities in form between the two equations.

1/G as a scalar field

What does it mean that 1/G is a scalar field? Paradoxically, it would mean that G is a varying gravitational constant – it need not be constant at all, and would likely change over time. In principle, it could also vary from location to location and time to time.

The idea that the gravitational constant depends on the distribution of mass in the universe does not fit into Einstein’s formulation of general relativity. It would be necessary to generalize that theory; the new theory would contain a scalar field in addition to the usual “metric field”, the mathematical object in which the geometry of spacetime (and, hence, gravity) is encoded. Mathematically, the metric field is an object called a “tensor” (to the mathematician, this designation expresses how geometry is viewed differently by different observers using different coordinate systems). Thus, theories that contain not only the metric field but also a scalar are collectively known as scalar-tensor theories.

In the framework of general relativity, the fact that the new field is a scalar is significant. In Einstein’s theory, the gravitational field can be “transformed away”. At least locally, gravity can be made to vanish. For example, consider a laboratory freely falling in the earth’s gravity field. An object released in the lab will remain “suspended” at a constant distance above the floor since the object and the floor are both accelerating toward the earth with the same acceleration. So, observers in the lab will declare that the object is “weightless,” and gravity has been “eliminated.” Actual observations such as this are in fact constantly experienced by the “weightless” astronauts in an orbiting satellite. More information about this can be found in the spotlight text The elevator, the rocket and gravity: The equivalence principle. A scalar field cannot be transformed away in a similar manner. Thus it possesses a type of permanence which would harmonize with its being dependent on an overall quantity such as the mass of the observable universe.

The path to scalar-tensor theories

It is one thing to hypothesize that, in general relativity, 1/G might be a scalar field. Actually formulating a theory describing the dynamics of such a scalar field is another matter. For this, the initial groundwork was laid by two scientists in pursuit of a completely different goal. In the early days (the first few years) of Einstein’s general theory of relativity, the German mathematician and physicist Theodor Kaluza and the Swedish physicist Oskar Klein suggested a unified description for Einsteinian gravity and electromagnetism – a model which was meant to describe these two interactions as consequences of one and the same generalized geometric structure. As it turns out, models of this type give rise not only to gravity and the electromagnetic field, but will automatically include an additional field, which plays the role of 1/G and satisfies an equation approximately similar to the one discussed above.

Kaluza-Klein theory was less successful at unifying gravity and electromagnetism than its creators thought, and did not become generally established. However, some of its ideas were taken up in the 1940s and 1950s in Germany by Pascual Jordan and his collaborators. Making use of the extra scalar field in one particular version of Kaluza-Klein theory, they developed a full scalar-tensor theory of gravity generalizing Einstein’s theory.

Independently (due to obvious lack of scientific communication between Germany and the US during World War II), Einstein, who by that time was at the Institute for Advanced Study in Princeton, New Jersey, and his assistant Peter Bergmann also came up with a scalar field related to G. However, Einstein did not pursue this idea, and existing work on scalar-tensor theories remained largely ignored in the United States until the late 1950s.

Next, the idea of a variable G made an appearance in Cambridge, where Dennis Sciama (later an influential relativist, then just a graduate student) proposed a model which could explain the fact that inertial forces appear only in reference frames accelerating relative to the distant fixed stars. Having a variable gravitational constant was not something Sciama intended. In fact, he proposed his model only as a suggestion of directions in which Mach’s principle, expressing inertial forces as gravitational ones, could be implemented. Yet as it turned out, one important consequence of Sciama’s model was the equation that we have encountered before, namely

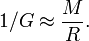
Sciama’s model was what physicists call a toy model – a simplified model that succeeds in capturing (and furthering our understanding of) one particular as- pect of a physical situation, but which does not manage to describe all important aspects of that situation. Sciama’s model only derived Newton’s law for a few special cases, and it did not lead to an easy way to describe the propagation of light. It did, however, shed a new light on Mach’s principle, and as such would prove to be an important stepping stone for later developments.

This brings us to Princeton University in the late 1950s, where Robert Dicke was a leading and very active advocate of re-examining standard general relativity, both theoretically and experimentally. In particular, guided by Sciama’s model and other ideas related to inertial forces as well, as well as by Dirac’s Large Numbers Hypothesis, Dicke suggested to me (Brans, then a graduate student in theoretical physics) to explore a model which would generalize standard Einstein theory by adding a “varying gravitational constant.” Dicke also suggested additional necessary conditions. First, the model was to preserve the conservation of energy-momentum. As in classical physics and in general relativity there should be no possibility for either energy or momentum to simply vanish, or to be created from nothing. Secondly, the model should result in an equation relating G to overall properties of the universe, similar to the equations already quoted.

At the time, I was not aware of the work of Jordan along these lines, and I developed my formalism independently until I was almost completely finished with my thesis in 1960. The resulting theories are properly called “Jordan- Brans-Dicke”, or simply JBD, theories. More generally, they are described as scalar-tensor (ST) theories.

The source of Einstein’s gravitational field is mass-energy (cf. the spotlight text Mass and More). In JBD theories, the scalar field, traditionally denoted by the Greek letter φ, also has mass-energy as its source (although there are differences – mass-energy associated with electromagnetic fields is a source of gravity, but does not directly contribute to the scalar field). From this, it can

be deduced that, looking at a sizeable part of the universe, φ ≈ M . Also, φ R appears approximately as 1/G in the equations describing mass as the source for gravity, leading to the equation 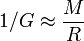with which the reader will by now be thoroughly familiar. Such theories present a major modeqification of Einstein’s general relativity.

A fundamental difference has already be mentioned: In such theories, not all gravitational effects can be eliminated as in the freely falling elevator. More practically, the predictions of scalar-tensor theories for phenomena such as the motion of bodies or the propagation of light in a gravitational field can vary from those of general relativity by terms inversely proportional to a dimensionless parameter, ω. In writing equations for an ST theory, I was faced with a familiar problem of “coupling” φ to gravity and matter. This requires what physicists call a “coupling constant.” Consequently (to the great consternation of Dicke!) our theory replaced one undetermined constant, G, by another, ω. There seems to be no way around this. Experimentalists can then use their results to set limits on ω. To date the results indicate that it must take values making ST theories practically indistinguishable from standard Einstein theory in the solar system context. However, as discussed below, these results do not interfere with the possible significance of ST, or ST-like, theories in the cosmological or quantum contexts.

The fall and rise of scalar fields

With their similar, but slightly different predictions for physical phenomena, scalar-tensor theories turned out to be the first significant challenge to Einstein’s theory in over forty years. Dicke’s prolific follow-up work spreading the news of such alternatives to Einstein’s theory stimulated others to seek and perform observations and measurements to try and distinguish between the two kinds of models. Coincidentally, NASA was at the time looking for significant experiments that would make use of the space program, and clearly, challenging Einstein’s theory was a tempting target.

What followed were experiments and observations which tested both the basic assumptions (such as the equivalence principle) of Einstein’s theory and its competitors and their specific predictions for the orbits of the planets and for the propagation of light within the solar system. As it turned out, standard Einstein theory fared better in these tests than any of the alternatives. In consequence, in the 1970’s, interest in these alternative theories dropped dramatically. However, from the 1980’s on, new discoveries and theories have led to renewed interest in scalar-tensor gravity.

In the context of cosmology, ever more evidence has emerged for a so-called inflationary phase in the very early universe. During such a phase, the cosmos would have undergone rapid, accelerated expansion. This helps to account for certain observable properties of our universe, such as its homogeneity at large scales. In current models, the inflationary expansion would be driven by a scalar field called an inflaton, which might be described by a modified Jordan-Brans-Dicke theory. A fundamental open questions of physics is that of quantum gravity – the ongoing search for a theory that reconciles the concepts of general relativity with those of quantum theory. One of the candidates for a theory of quantum gravity is string theory, which postulates that all the elementary particles known to physics are, if you look closely enough, different aspects of one and the same type of fundamental one-dimensional object, called a string. String theory incorporates gravity, but it is necessarily accompanied by a so-called dilaton, possibly a re-incarnation of the scalar field of scalar-tensor theory in an entirely different and unexpected context.

Given these developments, it might be that while scalar-tensor gravity is not needed to explain what astronomers observe within the solar system, it might well play a significant role in our understanding of the beginning of our cosmos, and of the most fundamental properties of matter.

Further Information