A Test Bed for the General Theory of Relativity

A model allows to describe systematically how well (or poorly) Einstein’s theory agrees with observations.

An article by Gerhard Schäfer

In a comparatively weak gravitational field by cosmic standards – for example, on our Earth or elsewhere in our solar system – the predictions of Newton’s theory of gravity and those of general relativity differ very little. Physicists are taking advantage of this by systematizing the transition from one theory to the other in a very useful manner: In the framework of the so-called post-Newtonian approximations, correction terms are added to the Newtonian theory step by step, which approximately take into account the deviations of Einstein’s theory from Newton’s (for more information on this, see the spotlight article Step by Step from Einstein to Newton).

The first step, in which only the most important correction terms are added, leads to the so-called first post-Newtonian approximation (1pN). It already contains descriptions of the light deflection in the gravitational field and the relativistic perihelion shift. This approximation is used, for example, in modern computer calculations of planetary orbits in the solar system, but also in the physics of orbiting neutron stars and gravitational lensing astronomy. But the first post-Newtonian approximation is important for another reason: It can be generalized to give a kind of test-bed for general relativity!

The way to the test theory

The general theory of relativity can be characterized as follows: In this theory Newton’s gravitation theory and special relativity theory are generalized and connected with each other; Einstein’s equivalence principle plays an important role.

Conversely, however, a whole series of theories satisfy this description, among which general relativity is admittedly the simplest. Another example of a theory based on the same foundations is the Jordan-Fierz-Brans-Dicke theory, often just called Brans-Dicke theory. In this theory, in addition to geometric gravity, there is another gravitational field called a scalar field. The scalar field affects both the motion of bodies and certain properties (the polarization) of gravitational waves.

Just as for general relativity, one can find a formulation for the other theories that starts with Newton’s theory of gravity and adds correction terms to it step by step. Comparison of the first post-Newtonian approximation of general relativity with that of the Brans-Dicke theory already reveals a difference: The correction terms have the same shape, with regards for example to their dependence on the masses of the involved bodies or on the gravitational constant, but the numerical prefactors of the individual terms deviate from each other.

However, this also means that – at least on the level of the first post-Newtonian approximation – one can create a kind of framework which contains all mentioned theories equally: One simply introduces a number of new parameters. For one of the correction expressions, for instance, general relativity provides a concrete shape which we want to abbreviate as X. This expression is now multiplied by a new parameter, which we will call δ (delta) here, so that there is now a new expression δ-X instead of the original one. We proceed similarly with the other correction terms – they each get a new parameter as a prefactor. For the special case that one sets all these parameters equal to one, one obtains the first post-Newtonian approximation of general relativity. For certain other values of the parameters, one obtains the post-Newtonian approximation of Brans-Dicke theory or one of the other alternative theories.

One can further extend the framework by introducing correction terms which do not appear in general relativity and which stand for phenomena that are entirely foreign to it. For example, corrections that arise under the assumption that there is a frame of reference favored by the laws of physics, a kind of “absolute space.” Other corrections come in when one assumes there are preferred directions in space, and that the outcome of certain physical experiments depends on how the experimental setup is oriented in space. Free parameters are written before these new correction terms. If these parameters are set to zero, the additional terms disappear, and one is back with the general theory of relativity.

This procedure leads to a generalized formalism which has been given the name parameterized post-Newtonian formalism, commonly abbreviated to PPN. The essential foundations of the PPN formalism were laid by Arthur Eddington, Howard Robertson, and Leonard Schiff; important recent contributions have been made by Kenneth Nordtvedt and Clifford Will.

The benefit of this generalization is that the new parameters allow us to quantitatively test general relativity.

For example, under the generalized theory, we can calculate the angle by which a beam of light is deflected as it passes the edge of the Sun and reaches an observer on Earth. For the angle, we then get exactly the same expression as in general relativity, but multiplied by a factor (1+γ)/2. Here, γ is a parameter that precedes one of the post-Newtonian correction terms and has the value 1 in general relativity. How much the light is actually deflected thus depends on γ, as can be seen in the animation below. It shows an object that is about 6000 times more compact than the Sun:

From measurements of the deflection angle for light deflection by the Sun, the value of the parameter γ can be directly determined, and one can quantitatively state how close this value is to the prediction of general relativity, i.e., to the value γ=1. Similarly, a number of other predictions of the test theory, such as for the anomalous perihelion rotation or the influence of spacetime on the axial direction of gyroscopes, explicitly contain the newly introduced parameters. By comparison with the measurements, the parameter values can therefore be determined empirically, and it can be quantitatively stated how well the parameter values obtained from the observations agree with the values (one or zero) required by general relativity.

The parameters of the test theory

In the following, we will briefly review each of the parameters of PPN theory and discuss a little of their physical significance.

Space curvature and γ (gamma)

The parameter γ has already been briefly mentioned. It describes the influence of matter on the curvature of space. In general relativity, the value of γ is one, but in Brans-Dicke theory, for example, the parameter is always less than one. If matter does not affect the curvature of space at all and space therefore has the Euclidean geometry familiar from school, even in the presence of matter, then γ=0. This is the case in Newtonian theory, for example.

Experimentally, the value of γ can be determined by measurements of light propagation (the gravitationally induced deflection of light as in the figure above or also the Shapiro effect). According to observations, γ deviates at most by a few hundred thousandths from the value predicted by general relativity. A selection of measured data is shown in the following figure:

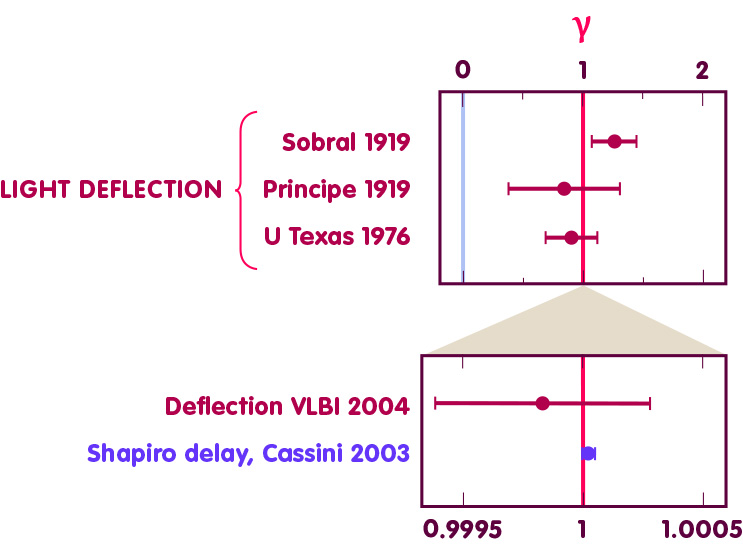
The upper diagram covers the range of values for γ from zero (Newtonian value, drawn as light blue line) to two. The lower diagram shows a detailed section in which γ does not deviate from one by more than a two-thousandth. Plotted in dark red are the results of measurements of light deflection: the first two measurements ever, made by the British solar eclipse expedition of 1919; an observation made by the University of Texas in 1973; and, in the bottom diagram, the 2004 measurement by S. Shapiro and colleagues on radio waves, which uses the high-precision VLBI method. The measurement point shown in purple corresponds to a measurement of the Shapiro effect using the Cassini spacecraft in 2003 and provides the most accurate determination of the γ parameter to date.

The gravity of gravity: β (beta) and ξ (Xi).

In addition to the already mentioned parameter γ, one introduces the parameter β, which equals one in general relativity, but can be unequal to one, for example, in theories with an additional scalar gravitational field. The parameter indicates how strong a gravitational field causes gravitation – an aspect of the so-called nonlinearity of gravitation (see the spotlight topic The Gravity of Gravity).

This nonlinearity can be noticed, for example, when it comes to calculating the orbit of the Earth’s moon and Mercury: In the correction terms, which play a role for this, β appears together with γ. In addition, the less important parameters α_1,2,3 and ζ₂ are also involved, to which we will return briefly below and which are zero in the framework of the general theory of relativity. The following figure shows Mercury’s orbit; its relativistic perihelion shift – the fact that the orbit is not an ellipse but rather rosette-shaped – is directly related to β and γ. In the figure, Mercury’s orbit is exaggerated in two ways to make the effect clearly visible: First, the eccentricity is increased by a factor of four, i.e., the deviation of the ellipse from a circular orbit is much stronger than in reality. On the other hand the perihelion rotation itself is enlarged by a factor of 200,000. The animation shows how the perihelion rotation changes as a function of the value of β:

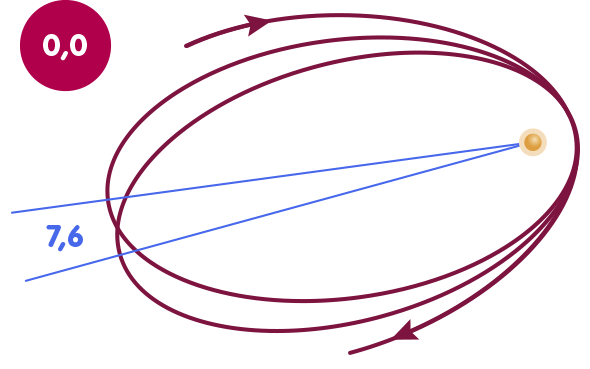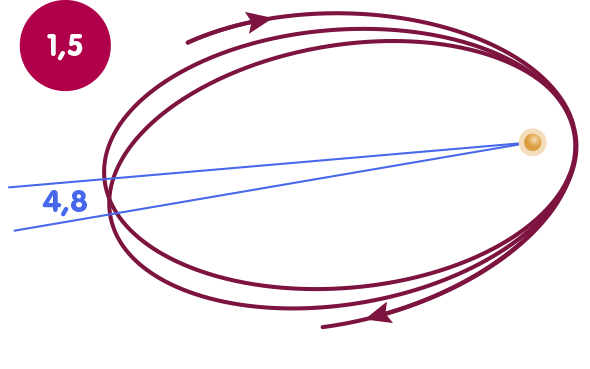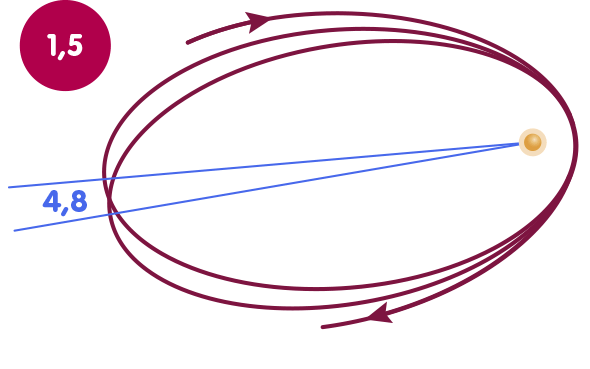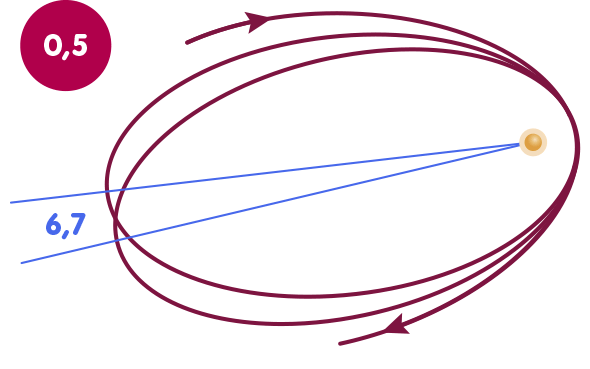
Accordingly, in order to determine β, one draws on measurements of the orbits of the celestial bodies mentioned. Let us consider a diagram in which each point stands for a particular pair of values for β and γ:

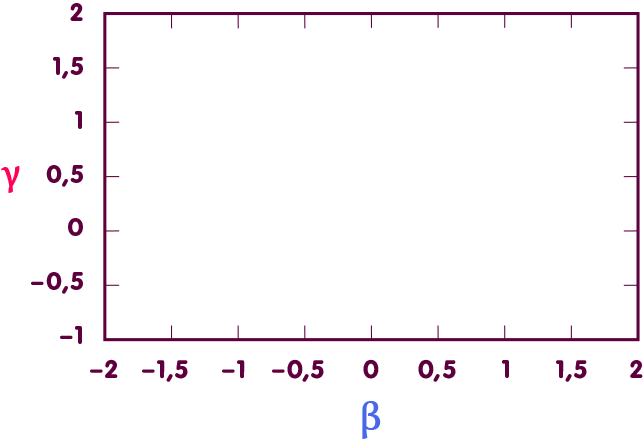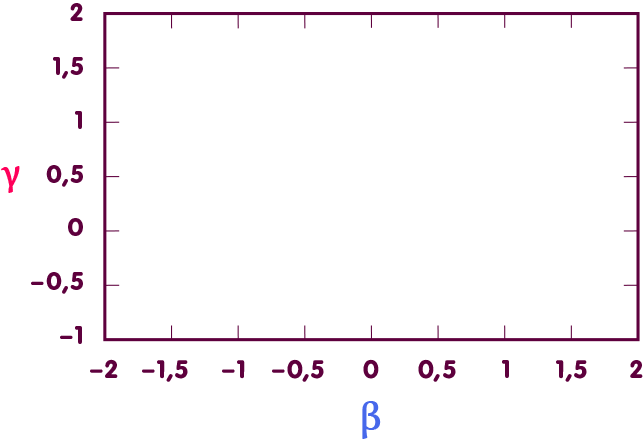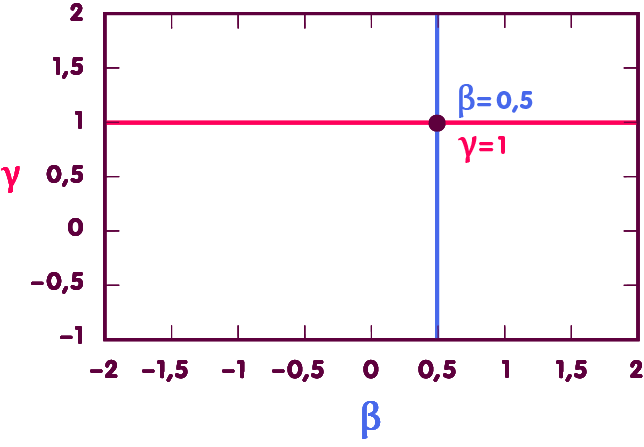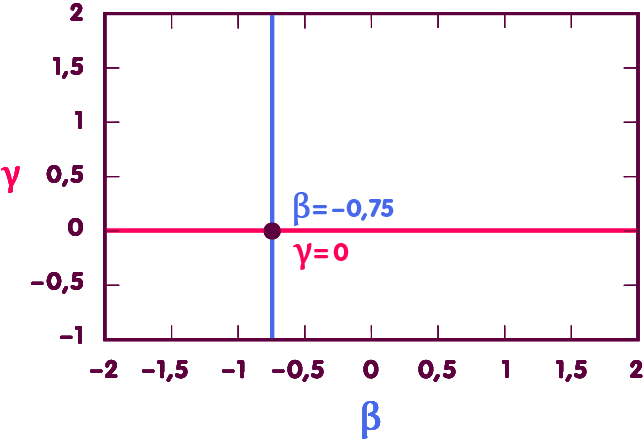
In such a diagram, the mentioned measurements define a straight line of admissible pairs of values (the purple line in the figure below). The fact that γ, see above, is known from further measurements defines another straight line of admissible values, which lies horizontally (red line). At the intersection of the straight lines lies the point corresponding to the actual values of β and γ – it is exactly at the value β=1 as predicted by the general theory of relativity (blue line):

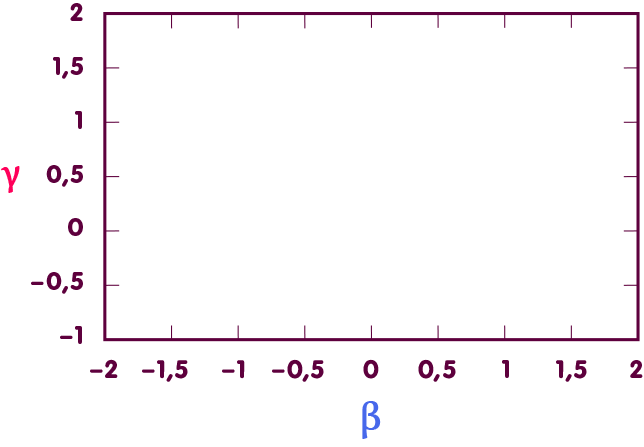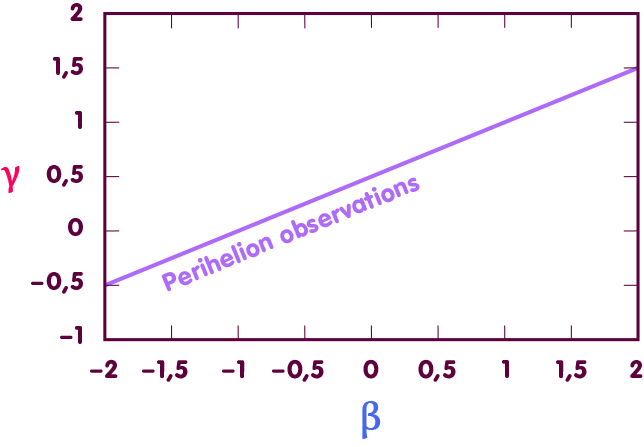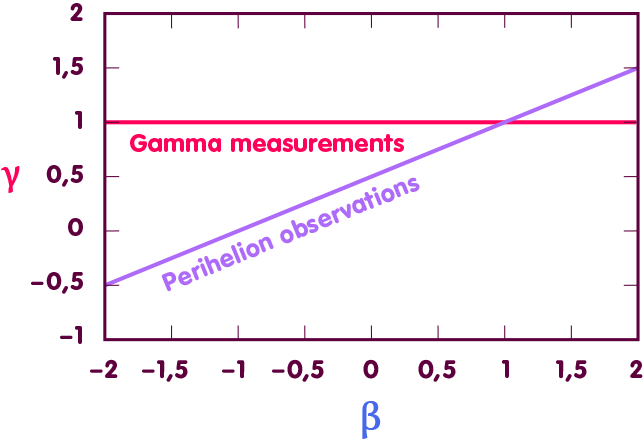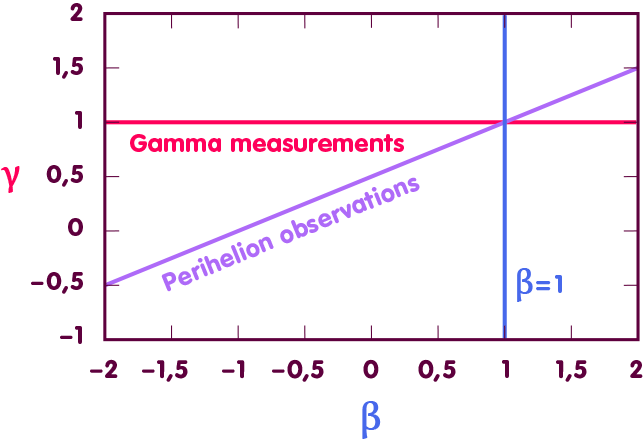
Accordingly, β deviates at most by a few ten-thousandths from the value predicted by general relativity.

Other observations are made regarding the motion of white dwarfs around neutron stars (pulsars) and both, in turn, in the gravitational field generated by all masses in our Galaxy. These are cases of much more strongly gravitating bodies, and these observations also provide constraints on the parameter values β and γ that are consistent with general relativity.

The value of the more exotic parameter ξ (Xi) deviates from zero precisely when gravity exhibits yet another form of nonlinearity than in general relativity (this is known in the literature as the effect of preferred locations). To this day, measurements have not provided any evidence that the value of ξ is different from the value of zero that general relativity predicts.

Preferred reference frames and conservation laws: αs and ζs

The parameters α₁, α₂, and α₃ describe different kinds of effects that indicate preferred reference frames – a kind of absolute space in which the laws of physics become especially simple for observers at rest relative to absolute space. They are all zero in general relativity.

The parameters ζ₁, ζ₂, ζ₃, and ζ₄ are also zero in general relativity. If either they or α₃ are non-zero, then conservation of energy and conservation of momentum are violated. Energy, for example, could then apparently be generated from nothing – which could be the case, for example, if there were long range interactions, unknown to us (and therefore not accounted for in the theory), through which energy would be transported into our solar system from other parts of the universe.

If all α- and ζ-parameters are equal to zero, then the angular momentum and center of gravity theorems still hold: angular momentum, a quantity associated with the rotation of bodies, can neither be created out of nothing nor annihilated, and the motion of the center of gravity of a system proceeds as if all external influences were directly acting on that point.

There is no evidence in observations and experiments that the values of α₁, α₂, α₃, ζ₁, ζ₂, ζ₃, and ζ₄ are different from zero.

A special case: time dilation and α (alpha)

Sometimes tests of general relativity also use a parameter α that is not one of the PPN parameters but, like them, can be used to test certain predictions of general relativity. It is directly related to the influence of gravity on time.

α has the value one in the general relativity, too (as well as the PPN parameters β and γ). As far as the motion of bodies in the gravitational field is concerned, however, the term in question does not belong to the corrections which are added only by general relativity, but it is already part of Newton’s equations. Accordingly, it is already well known from the conventional observations of the planetary orbits that it is indeed the term predicted by Newton and Einstein.

The reason to introduce α as a free parameter nevertheless is that the term in question plays a double role in the general theory of relativity and, apart from the motion of bodies, is additionally responsible for effects which are foreign to Newton’s theory. These effects are the (well measurable) frequency change of light in the gravitational field and the directly related clock rate difference (gravitational time dilation). The measurement of these effects provides a highly accurate access to the measurement of α – and this parameter, in turn, offers the possibility to express quantitatively how well the predictions of general relativity on gravitational frequency shift and time dilation agree with observations. The figure below shows some selected measurements for the determination of α:

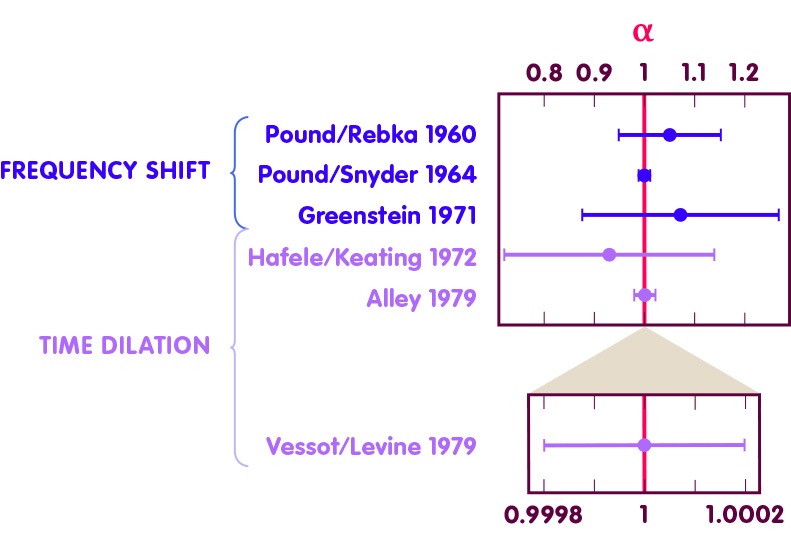
The figure shows measurements of the frequency shift (blue data points) and measurements where time dilation is measured using atomic clocks (light purple data points). The experiments of Pound and coworkers determined the frequency shift in the laboratory using gamma rays (and using so-called Mössbauer spectroscopy on atomic nuclei of the isotope iron-57). Greenstein and colleagues evaluated astronomical observations of the white dwarf star Sirius B. Hafele/Keating and Alley launched atomic clocks from Earth using airplanes. The most accurate readings came from Vessot and Levine’s 1976 experiment, called Gravity Probe-A, in which a highly accurate maser clock traveled aloft in a rocket. The accuracy is so high that the error bar can only be seen in the detail section of the diagram below. The experiment showed that the value of α agrees with the prediction of general relativity to an accuracy of almost one ten-thousandth.

Once α has been introduced, the coefficient of the angle of deflection of light in the gravitational field of the Sun shown above also has a slightly different form – instead of the (1+γ)/2 mentioned there, it is then (α+γ)/2.

As useful as α is in measurements of frequency shift and time dilation – in modern measurements for the accuracy of general relativity, the results of these experiments are assumed, and one calculates a priori with α equal to one.

Outlook

In total, there are ten parameters in the parameterized post-Newtonian formalism (eleven if one adds the outsider α). As many as eight of these parameters are zero in general relativity – indicative of the virtually minimalist nature of the theory as the simplest generalization of Newton’s theory of gravity that is consistent with observations.

In particular, those parameters that do not vanish in general relativity – γ, β, and the outsider α – play a crucial role when it comes to evaluating observations and experiments from the domain of general relativity. The results are then often directly expressed by these parameters – for example, if it is about observations of the deflection of light, one will often be able to read as a conclusion a statement like that, the observations led to γ=0.99983 ± 0.00045, i.e. to a certain value for γ, which as usual is afflicted with a certain measurement inaccuracy.

As briefly mentioned at the beginning, the PPN formalism takes into account only the simplest correction terms to the Newtonian theory of gravity – the so-called first post-Newtonian approximation (1pN). For the sake of completeness, it should be noted that there are certain generalizations to the next level of the post-Newtonian approximation (2pN), where significantly more terms are considered. However, this generalization does not cover all conceivable models, but is mainly limited to the special case of bodies moving in the mutual gravitational field, but not rotating very fast around their own axis.

Further Information