Inertial and Gravitational Mass

About the different roles played by mass, and the weak equivalence principle

An article by Markus Pössel

In classical physics, mass plays a curious double role, which is responsible for a peculiar difference between gravitation and all other forces. This difference, in turn, was Einstein’s starting point in developing his theory of gravity, space and time: general relativity.

Mass and inertia

Mass is a measure of a body’s inertia. Imagine that I’m in empty space, properly suited up, far away from all major sources of gravity. I’m standind on the outside of a space station, safely held in place by clamps fixing me to the station’s hull. Next to me, a box and a small ball are floating in space. Now I give the ball a shove and, afterwards, the box, taking care to exert exactly the same strength both time. The ball reacts to my shove by accelerating and flying away at high speed. The box hardly reacts at all. It does drift away from me, but only very slowly.

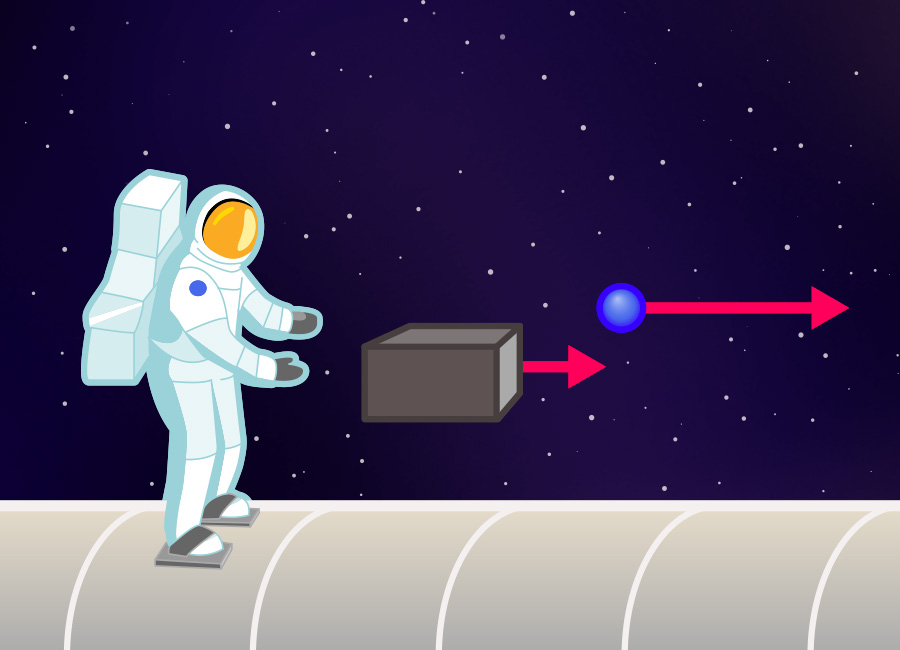
The difference between ball and box? The box’s significantly greater mass, which is responsible for the box reacting so much more diffidently than the ball to the same amount of shoving.

While this example gives a rough idea of what inertial mass is all about, it doesn’t lead directly to a definition: to quantify mass in this way, we would need to define when two shoves have the same strength. Instead, it is more useful to look at simple collisions between different bodies. In outer space, it would be sufficient to have these objects float towards each other. In the laboratory, one would first need to eliminate friction. Your typical high-school physics laboratory probably has an air track on which gliders will move almost without friction, which will do the trick.

The easiest case is a head-on collision between two spherically symmetric objects. These objects move along a single line before and after the collision:

In general, the collision will change the speeds of the spheres. Let’s call the first object’s change in speed Δv₁, and the second one’s Δv₂, where each time, the change is defined as the object’s speed before the collision minus its speed afterwards. If you make this experiment, you will find that the ratio between those two changes in speed is independent of the object’s initial speeds. In other words: this ratio depends only on the object’s themselves, not on their motion. We can use this fact to define the masses of the two objects, using the relation

where the minus sign is necessary to obtain a positive ratio. As soon as we have defined the unit of mass (in other words, chosen one particular body as a standard), we can make experimental collisions and thus determine the masses of all other bodies.

This definition is consistent with our everyday notion of larger and smaller masses (or larger and smaller inertia, respectively). If, say, the first body’s mass is much greater than the second body’s, then the left-hand side of the above equation is a large number. In consequence, the collision is going to cause the speed of the first body by a comparatively small amount, compared with the change in the second body’s speed. The animation above shows an example: Before the collision, the cyan and ball and the violet one are moving towards each other equally fast, but in opposite directions. However, the mass of the cyan ball is just a quarter that of the violet one. While the collision hardly affects the more massive ball – a little slowing down, that’s all – the cyan ball’s speed changes quite drastically: it bounces and moves back into the direction it came from, and at significantly higher speed than before.

Inertia and forces

The mass we have defined in this way plays a key role in classical mechanics – that is, in the laws that describe how objects move under the influence of forces. As millions of high-school students have witnessed, one can measure the strength of a force using suitably chosen springs: The elongation of a spring is a measure for the strength of the force acting on it – at least in cases where the spring’s deformation stays within certain limits:

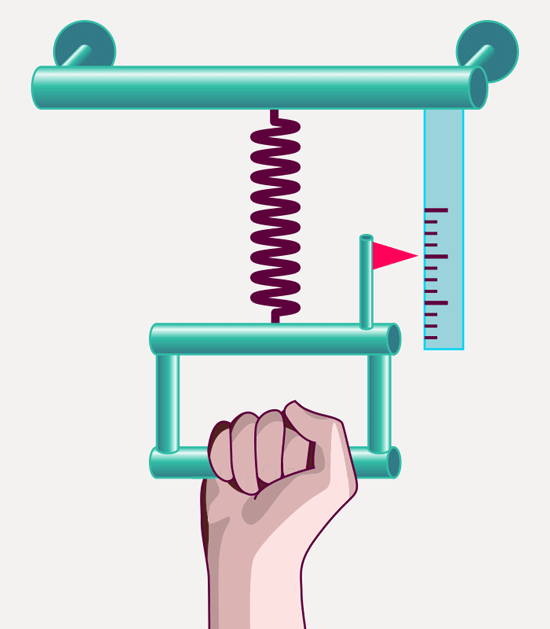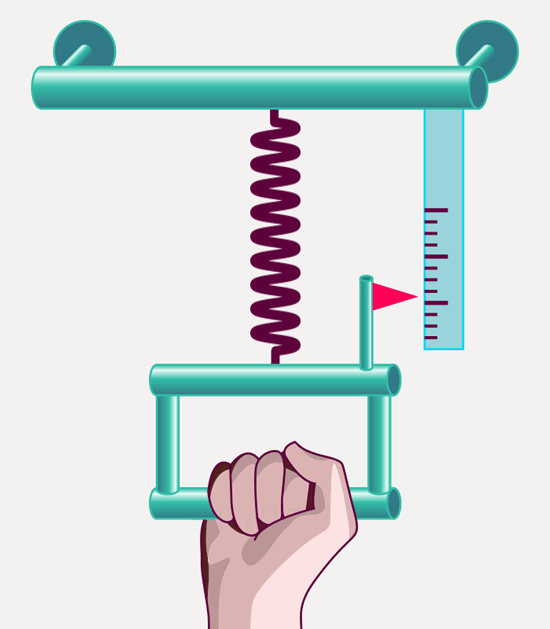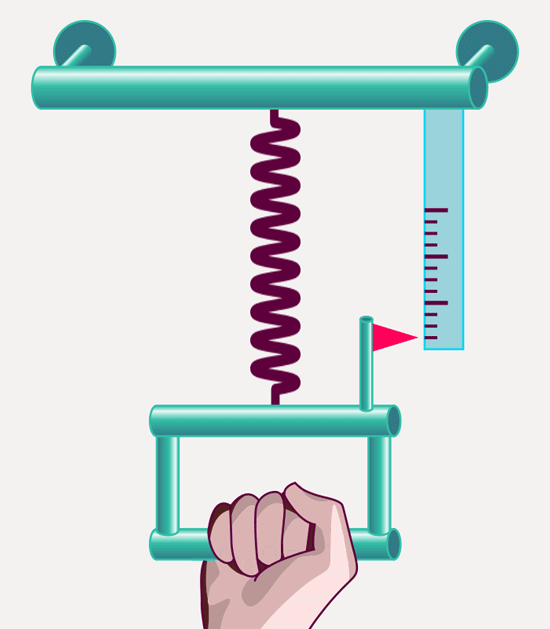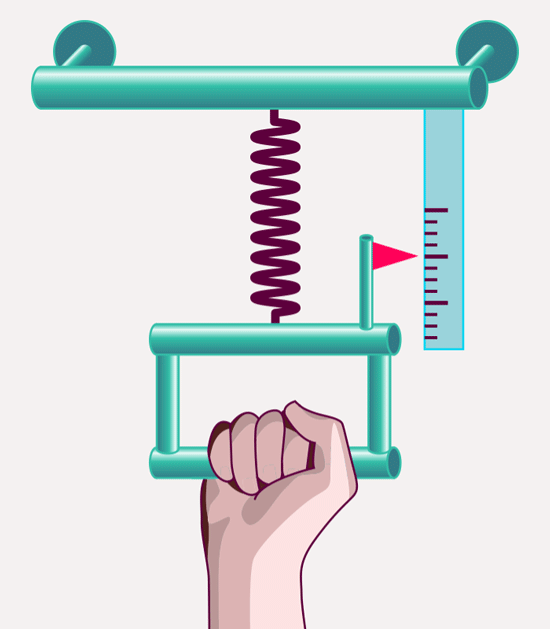
The definition meshes with our everyday ideas of when forces are strong: pull more strongly, and the spring will be stretched further than by a weaker pull. But the definition can do more than your subjective feeling of when a force is weaker and when it is stronger: It allows you to determine the ration of force strengths – we can measure when a force is two times, three times, four times as strong as another.

Newton’s second law of motion establishes a relation between the strength of the force acting on s body and the body’s acceleration. The shorthand version is

Force = Mass · Acceleration

or, if you write it the other way around,

Acceleration = Force / Mass.

This last form of the equation is another way of saying that ball and box, pushed by me using the same force over the same period of time, will accelerate in different ways: The ball’s mass is much smaller, and “Force divided by mass”, that is, the ball’s acceleration, is markedly greater than that of the box.

Gravity: Equal acceleration for all

Gravity is special. Take two objects and let them fall, taking care to release them at the same time. They will fall side by side, accelerating in exactly the same way – at least if you’ve been thoughtful enough to let them fall in a vacuum chamber, eliminating the effects of air resistance. Whether you’re using a feather or a lead weight – after one second, the object will have reached a speed of roughly 10 metres per second, after two seconds, it will have accelerated to 20 metres per second. If you release feather and lead weight at the same height, at the same time, they will stay next to each other as they fall:

This is known as the universality of free fall: Gravitational acceleration is the same for all objects. In particular, it does not depends on the objects’ masses.

On cosmic scales, the situation is very similar. Consider smaller objects orbiting a central mass, the most important example being the planets of our Solar System orbiting the Sun. If you neglect the smaller masses’ gravitational attraction – not a big “if”, since that attraction does not make much of a difference, the Sun’s attraction being so much bigger – the result is the same: The gravitational acceleration experienced by any of these small bodies is independent of their intrinsic properties, and in particular independent of their mass. With one important difference: In this more general case, the gravitational attraction will depend on the smaller body’s location, namely on its distance from the central mass. Closer to the central mass, gravitational acceleration is stronger; further away, it is weaker.

Mass as gravitational charge

You might say that’s just how it is: Gravitation results in acceleration. Free fall is universal. But in one respect, that fact is highly unusual and remarkable, namely when you decide to describe gravity as a force – that is, describe it in the same way you would describe other interactions, such as friction, the elastic forces of a stretched spring, electric or magnetic forces. If all you’re after is the approximate description of planetary orbits, you don’t need to bother with forces. But if you want to calculate when there’s a balance between gravity and other influences – say, how strong a spring you need to suspend a given mass here on Earth, or how strong a wall needs to be to support a roof against gravity – then it is quite useful to describe gravity as a force.

You can measure the gravitational force in the same way we have quantified other forces, using a spring arrangement: instead of pulling on the spring, we simply attach an object and let gravity do the pulling:

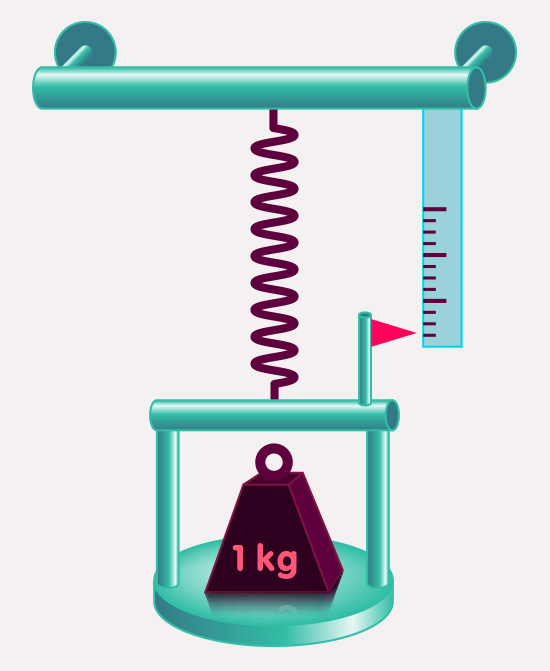
The elongation of the spring tells us the strength of the gravitational force pulling the object towards the ground. This gravitational force is called the object’s weight.

But we already know that this force results in the same acceleration for all freely falling bodies. We already discussed how the acceleration caused by a force is

Acceleration = Force / (inertial Mass).

For the acceleration to be the same for all objects, the force must depend on the object’s mass, more concretely: the gravitational force, e.g. the one exerted by Earth on each falling objects, needs to be proportional to each object’s mass. Written as a formula,

Gravitational force = Mass · g,

where g is a factor that does not depends on any of the object’s intrinsic properties. If this formula holds, then, when we calculate the acceleration, the following happens:

Acceleration = Gravitational force / Mass = (Masse · g) / Masse = g

– the object’s mass drops out, and what is left is the same for all objects: the acceleration g. The quantity g is known as the gravitational acceleration, and its value is approximately the same on (and near) the surface of the Earth.

The proportionality between the gravitational force acting on a body – the body’s weight – and its mass has numerous practical applications. We weigh objects, such as foodstuffs, to determine their mass, that is, to determine how much of a given foodstuff we are getting (or, equivalently, need to pay for). This is such a common way of determining mass that, in countries using the metric system, scales of a balance are routinely marked in units of mass. Regrettably, this leads to statements that, physically, are nonsense. Saying “the weight of this object is one kilogram” is just wrong – weight is a force, and should be specified in units of force; the kilogram, on the other hand, is a unit of mass. The only reason that statements make sense in everyday life is that, a body’s weight is directly proportional to its mass, with the proportionality factor, the gravitational acceleration, nearly constant on or near the surface of the Earth.

Countries using the imperial system have a different problem. There, the “pound” is both a unit of mass and of force. In everyday life, which we spent on or near the Earth’s surface, this works because a body’s mass and weight are proportional. In more general situation, one needs to split the ambiguous unit in two, resulting, somewhat awkwardly, in a unit pound-mass for mass and a unit pound-force for force.

When it comes to forces or fields, it is anything but unusual for the force acting on an object to be proportional to a specific intrinsic property of the object. This property is known as the object’s charge with respect to the force in question. For instance, the electric force acting on an object is equal to the produce of the object’s electric charge and a quantity that is independent of the object, namely the electric field.

We’ve seen that the gravitational force acting on an object is the product of the object’s mass and an object-independent quantity, the gravitational acceleration. Put differently: Mass is a kind of gravitational charge.

Mass as a source of gravity

Mass has yet another role to play. So far, we’ve introduced the gravitational charge as a measure for how strongly an object reacts to the gravitational pull of other bodies (e.g. to the Earth’s gravitational pull). But an object’s charge also determines the force exerted by that object on other objects. In the case of gravity, mass as the gravitational charge also determines the force exerted by an object on other bodies. If we want to differentiate between the two roles, we can talk about active and passive charge: Active charge determines the force exerted by an object, passive charge determines how strongly it reacts to the influence of other objects. For instance, the active gravitational charge of Sun can be measured by observations of planetary orbits. The active gravitational charge of a metal sphere can be measured in an experiment named after the physicist Henry Cavendish. The basic setup is shown here:

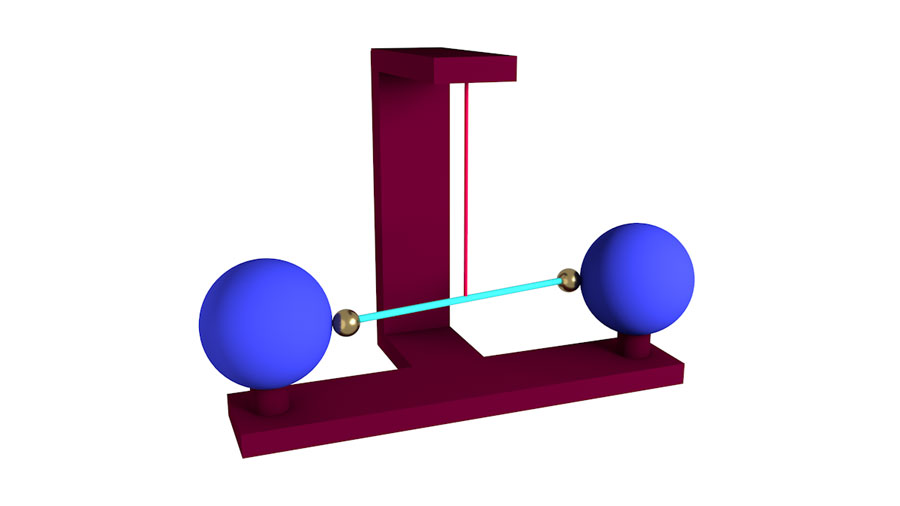
The smaller spheres (in the figure: gold-colored) are attached to a rigid rod (green). They are gravitationally attracted to the larger test masses (black) – however, there’s also the torsion wire (red) to which the rod is attached: this wire resists when you try to twist it.

The active gravitational mass is also proportional to the mass. The factor of proportionality is called the gravitational constant. You can determine it using a metal sphere if you measure its mass and then do the Cavendish experiment.

Three kinds of mass

Mass plays a triple role, then: as an active and a passive charge, and as a measure for a body’s inertia. Or, instead of one physical quantity with three facets, could we be looking at three different physical quantities? Inertial mass as a measure of inertia, and two types of gravitational charge: passive gravitational mass to determine the strength of the object’s reactions to gravitational attraction, and the active gravitational mass that characterizes the attraction exerted by the object on other bodies?

We do not have to make this distinction, but there’s at least one reason to do so: it’s a necessary first step if you want to test whether or not these different types of mass are, in the final analysis, the same. Quite a number of experiments have been made to look for possible differences between inertial and passive gravitational mass. So far, no differences have been found. In comparison, there have been very few experiments looking for differences between active and passive gravitational mass. Here, too, all the available evidence indicates that the two are, indeed, the same.

General relativity and the weak equivalence principle

In classical physics, it’s not clear why (passive) gravitational and inertial mass should be the same. In Einstein’s theory of gravity, general relativity, the situation is different. There, the reaction of small bodies to gravitational attraction is purely geometrical: Massive bodies will distort space and time, and moving bodies follow the straightest paths possible in such a distorted spacetime. The artificial distinction connected with the concept of a force – inertial mass on the one hand, gravitational mass on the other – is replaced by a law that has the equality of all bodies built-in at the lowest level: That, in a given situation, all bodies experience the same gravitational acceleration is due to the fact that their motion is directly governed by the properties of their spacetime environment; the object’s intrinsic properties play no role at all.

Conversely, the fact that all objects experience the same gravitational acceleration is a necessary precondition for Einstein’s geometric description. In this context, the universality of free fall is called the “weak equivalence principle” (a special case of Einstein’s more general equivalence principle), and in some form or other you will encounter it at the very beginning of systematic expositions of general relativity.

Further Information