From soap bubbles to Einstein

Most readers will know them from childhood: soap bubbles

An article by Bernhard List

[© Daniele Levis Pelusi, unsplash]

But children are not the only ones who are interested in soap bubbles. These fragile entities have captured the imagination of mathematicians, as well. From their physicist colleagues, mathematicians know which forces act on a soap bubble. Namely, there are tension forces between the molecules of the soapy skin, aimed at keeping the surface of the bubble as small as possible, while the volume of the bubble stays constant.

The math of soap bubbles

Mathematically speaking, the question of what shape the surface of a soap bubble should have is a minimization problem (the surface area must be as small as possible) with a constraint (the volume must remain constant). For this kind of problem, mathematics offers versatile tools, collectively known as the calculus of variations, with which mathematicians can derive an equation that characterizes the surfaces of soap bubbles. From these equations, one can derive that the only solutions in ordinary three-dimensional space (more precisely: in Euclidean space) are spherical surfaces. That is the mathematical reason behind the fact that soap bubbles are spherical. (However, for real soap bubbles here on Earth, this solution is only an approximation, as it does not take into account the effect of the Earth’s gravity. In a space station, far away from all masses and their gravitational influence, soap bubbles should be perfect spheres.)

The question becomes more complicated if we take metal wire, bent into certain shapes, and dip it into soap suds – what is the shape of the soapy skin that forms along the wire?

Square-shaped and tetrahedron-shaped wire-frames with soap-bubbles
[© S. Aulig, Universität Paderborn]

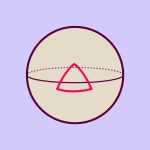
The Plateau problem

This is known as the Plateau problem, named after the Belgian physicist Joseph Antoine Ferdinand Plateau. Mathematically speaking, this is another minimization problem. However, this time there are boundary conditions – the boundaries of the soap-skin must lie on a given wire-frame. Surfaces that solve this problem are called minimal surfaces. The following picture shows one of many possible examples:

[© GRAPE Minimal Surface Library]

So what’s the connection with Einstein and his theories? In short: mathematics. The structure of the equations obeyed by minimal surfaces or soap bubbles is eerily similar to that of Einstein’s equations, the centerpiece of his general theory of relativity. To be sure, there are differences as well – for instance, the spacetimes of general relativity are intrinsically distorted, while minimal surfaces are distorted surfaces embedded in a higher-dimensional space. But there are strong analogies between the two geometrical situations, and many methods of finding solutions or studying properties of equations can be used in both contexts. Results from the theory of minimal surfaces give information that is important for analyzing solutions to Einstein’s equations, and vice versa. Whoever finds an interesting soap-skin shape might, at the same time, have discovered important information about simple model universes in Einstein’s theory. That’s why, at institutes like the Albert-Einstein-Institute, you can find mathematicians working on both superficially dissimilar problems – on abstract models of the universe and on questions from the world of soap bubbles.

Further Information